考虑AGV避碰的自动化码头多资源协同调度
杨雅洁,苌道方,余 芳
上海海事大学 物流科学与工程研究院,上海201306
1 引言
随着经济快速发展,海运贸易量不断增大,如何提高效率是各个码头亟待解决的问题。新型自动化码头开始陆续建成,AGV 是连接岸桥和场桥的重要设备,其作业效率的高低对整个码头的运营效率起着关键性作用。另一方面,由于码头的特殊性,其各个环节之间是相互耦合的,如何实现各个资源间的合理调度,对提高自动化码头的作业效率有非常重要的意义。
目前,众多国内外学者对码头资源中两个资源的协同调度研究占了多数,一般有岸桥与集卡、泊位与岸桥、集卡与场桥的调度。岸桥与集卡的研究有:马超等[1]针对集装箱岸桥与集卡的协同调度问题,考虑集卡路径约束和岸桥实际操作情况,构建边装边卸的混合整数模型,用分层方法遗传算法来求解模型;张笑等[2]针对集装箱在码头堆场分区堆放的情况和码头泊位装卸作业的状态要求,以岸桥和集卡作业时间最小建立模型,通过Gurobi 实现集卡路径优化;梁承姬等[3]考虑集装箱装卸作业顺序和岸桥干涉等建立最大完工时间最小化目标的混合整数规划模型,最后用遗传算法和粒子群算法求解,并比较了其优劣性;余孟齐等[4]考虑集装箱之间的优先关系和岸桥安全边际的实际约束,建立混合整数规划模型,并用改进粒子群算法对其进行求解;严南南等[5]针对环境污染和能源紧缺问题,建立了一个考虑能耗的岸桥和集卡调度的多目标数学模型,用遗传算法采用MATLAB求解,使用多目标方法平衡能耗和时间这两个目标。陈宁等[6]考虑集装箱作业过程不交叉、优先级约束等因素,采用混合流水车间作业调度方法建立混合整数规划模型,获得集装箱任务的岸桥和AGV 分配及集装箱任务的处理顺序。
虽然在两两协同调度方面的研究取得了很多成果,但是,单纯的对局部某个模块进行优化不一定能改善整个码头的生产效率。因此,三个及以上资源间的调度开始备受重视,比如:岸桥-集卡-场桥协同调度,集卡-场桥-堆场协同调度。马越汇等[7]将自动化集装箱码头的不确定因素考虑进去,建立AGV、岸桥、堆场、龙门吊四者最末结束任务时间最小化为目标函数的模型,判断不确定因素对最末任务结束时间的影响;徐远琴等[8]考虑装卸不平衡问题,对集卡运输时间与岸桥、场桥等待时间加入权重参数建立模型,用算例验证模型的有效性和实用性;杨勇生等[9]考虑双小车岸桥和双轨道龙门起重机,以卸船作业最小完工时间为目标建立混合整数规划模型,运用遗传算法求解给出自动化码头的设备调度优化方案;添玉等[10]引入岸桥调度任务为主要约束,构建岸桥、顶升式自动导引车及自动轨道吊的协同调度模型,采用遗传算法实现系统效率的提升下的作业序列的最优化;luo 等[11]考虑自动化集装箱卸载过程,制定混合整数规划模型,运用遗传算法求解,有效减少船舶在港时间;Wang 等[12]同时考虑集装箱码头装载和卸载活动的问题,用MIP 模型描述车辆调度,堆场起重机调度和集装箱存储位置之间的相互关系,小规模用CPLEX 求解,大规模用遗传算法求解,有效减少集装箱任务的完成时间来缩短船舶周转时间。Kaveshgar 等[13]考虑岸桥干扰,集装箱之间的优先级关系建立综合优化模型,运用遗传算法和贪心算法相结合求解,能够合理解决集装箱码头出现的运营问题。上述文献都在三个及以上资源的协同调度研究中做出了一定的贡献,但是目前尚未有文献在考虑多个资源协同调度的同时考虑了AGV 行驶过程中的碰撞问题。在自动化码头中,AGV 行驶路径比较固定,不像传统集卡行驶灵活,容易发生拥堵,对于多AGV 同时运行的碰撞问题亟待解决。因此,本文在考虑三个资源(岸桥、AGV、场桥)协同调度的同时考虑了AGV 间的碰撞问题。另一方面,现有的文献,都是考虑在任意时间只能通过一辆AGV 来减少等待时间,如容芷君[14]在处理碰撞问题时,赋予小车优先级别,优先级最高的先通过,其余小车选择等待;吴晓雨[15]在解决多AGV 路径规划时,提出等待避让和更改路径两种选择,凌忠奇[16]提出在AGV 节点间发生冲突时,采用等待策略,优先级高的AGV 先通过。而本文模拟实际交通的情况,通过对AGV 通过的路口设置相容和冲突相位,处于相容相位的AGV 能够同时通过,可以使路口同时通过多辆AGV,以此来缩短整个作业流程时间。
2 问题描述
本文研究自动化码头的范围包含岸桥作业区、AGV水平作业区、堆场箱区。随着港口业务量增多,自动化码头逐渐成为各个码头的建设的目标。AGV 作为自动化码头的象征性产物,为了满足日益增长的业务需求,自动化码头AGV 的数量也随之不断增多。而其固定的行驶路线增加了冲突的概率,导致AGV 拥堵事件频发,直接影响了整个码头的作业效率。因此,如何实现考虑AGV避碰情况下的多资源间的协同调度问题亟待解决。

图1 集装箱作业流程图
本文针对岸桥-AGV-场桥三个资源协同调度情况下AGV 的避碰问题(主要考虑AGV 在十字路口的避碰)。整个作业流程如图1 所示,AGV 从岸桥1 下的交接点等待岸桥将进口集装箱从船上卸载到AGV 上,再由AGV 选择最优路径(如图1 中路径1 所示)将任务送到场桥前侧交接点,AGV 便可自由返回码头处理下一集装箱。本文结合岸桥、AGV、场桥三个资源,同时考虑路径的分配及AGV 的避碰,建立一个所有任务的最大完工时间最小化为目标的混合整数规划模型。
3 模型建立
3.1 模型假设
根据码头的一些实际情况,如在自动化码头中,随着AGV 数量增多,在路口冲突问题最为显著;场桥前设有AGV 伴侣,AGV 将任务放下即可返回[17]。为了便于问题求解分析以及集装箱码头作业规则,对问题进行相应的假设:
(1)岸桥处理单个集装箱任务的时间固定。
(2)AGV从岸桥取箱时间忽略不计。
(3)AGV 均匀速行驶,双车道路径,只考虑其在十字路口的碰撞。
(4)已知进口集装箱任务在堆场的存放位置。
(5)场桥从AGV 伴侣取箱时间忽略不计,场桥处理集装箱的时间固定。
(6)AGV 放置场桥前侧等待区即可离开返回岸边执行下一任务。
3.2 模型参数与决策变量
3.2.1 模型参数
I:所有任务的集合,i=1,2, ,Ι。
K:岸桥的集合,k=1,2, ,Κ。
B:箱区的集合。
V:AGV的集合,v=1,2, ,V。
Fi:任务i的结束时间。
QSi:岸桥开始任务i时刻。
YFi:场桥结束任务i时刻。
TUik:岸桥k开始处理任务i的时刻。
TSikv:AGVv开始执行岸桥k第i个任务的时刻。
Tkb:AGVv 从岸桥k 到箱区交接区b 所需要的时间。
TDiy:场桥Y 开始处理任务i的时刻。
T1:岸桥处理单个任务所需要的时间。
T2:场桥处理单个任务所需要的时间。
dvt:AGVv在t 时刻的相位。
3.2.2 决策变量


3.3 基本模型
3.3.1 AGV路径选择与避碰模型
AGV 在行驶过程中,将会首先选择一条路径,如果选择的路径中AGV 会同时经过某个十字路口,则需要对AGV 进行路口相容还是冲突的判断。传统的模型大多假设只允许优先级最高的1 辆AGV 通过十字路口以避免冲突,而本文通过对路口的每个相位都设置相容和冲突的相位,处于相容相位的AGV 可以同时通过而不发生碰撞,而处于相冲突相位的AGV 则不能同时经过路口,以避免发生碰撞。例如,图2 为t 时刻AGVv 到达双车道十字路口时,12 种方位的情况。假设相位=1,可以从图2中看出相位1的冲突相位为相位4,5,8,10,11,则Pdvt={4,5,8,10,11}。即在t 时刻,当AGVv 行驶到相位1 时,其他小车如处于4 相位,会发生碰撞冲突,则不能与其同时通过;如处于6 相位,则两个AGV 相容,可以同时通过,节约路口等待时间。这样可以使路口能同时通过多辆AGV 而不发生碰撞,大大提高了AGV 的运行效率,缩短了整个任务完成的时间。

图2 十字路口AGV相位图
3.3.2 协同调度模型
本文以总任务最大完工时间最小化为目标,考虑如何将任务分配给岸桥、AGV、场桥。首先,采用随机方法将各集装箱任务分配给各岸桥,考虑一个集装箱任务在任意时刻只能分配给一个岸桥、一个AGV。然后由AGV 选择最优线路,所谓最优线路,即使AGV 完成所有任务之后,已知各个岸桥到各箱区的距离,AGV 匀速行驶,方能计算出运行时间。将各集装箱任务送至目标场桥,AGV 返回需要执行下个任务的岸桥(除AGV 完成最后一个任务外),算是一个任务真正完成的时间,直至最后一个任务完成为止。
结合3.3.1 小节所提出的避碰模型,将AGV 避碰加入岸桥、AGV、场桥协同调度模型中,建立一个总任务最大完工时间最小化的混合整数规划模型。具体模型如下:

其中,式(1)为目标函数,表示最小化所有任务的最大完工时间;式(2)表示所有任务的完工时间;式(3)表示任务的结束时间;式(4)表示任务的开始时间;式(5)表示每个任务在任意时刻只能分配给一个岸桥;式(6)表示岸桥在任意时刻只能被分配一个任务;式(7)表示任意任务只能分配给一个箱区;式(8)表示每个集装箱任务在任意时刻只能由一个AGV 完成;式(9)表示在任意时刻每辆AGV只能完成一个集装箱任务;式(10)和式(11)是避免两个处于冲突相位的AGV 同时经过十字路口;式(12)表示场桥只能在AGVv 将集装箱运输到指定工作点后才能开始处理集装箱;式(13)表示只有在岸桥将集装箱放到AGV 后,AGV 才能开始处理任务;式(14)表示任务i的完成时刻;式(15)是对参数的非负限制。
本模型中,AGV 服务任意岸桥,当AGV 开始运作后,将任务送至目标箱区即可返回。返回取任务的原则(优先级最高的先取),给集装箱任务设置了优先级,数字越大,优先级越高,到最后一个任务完成,即所有任务完成的时间。在AGV 行进过程中,需要判断路口是否存在冲突碰撞(选定目标点,各路口到目标点距离已知,若在同一时间点距离目标点路程相同,则会在该路口发生冲突)。传统的模型并不考虑避碰规则,而是选择运送任务优先级低的AGV 等待,优先级高的AGV 优先通过。而本文提出的模型考虑了避碰规则,当AGV 发生冲突时先判断是否处于相容相位,如果处于相容相位,则可顺利通过,如判断处于冲突相位,则运送任务优先级低的任务等待,从而节约总任务等待时间。
4 算例分析
为了评估模型的准确性,首先对参数进行初步设定,采用JAVA编程语言进行精确求解,对各算例进行分析。本文考虑了两种情况:(1)不考虑避碰规则下岸桥-AGV-场桥的协同调度;(2)考虑避碰规则情况下的岸桥-AGV-场桥的协同调度,然后分别对两种情况下不同卸箱任务数量、不同岸桥-AGV-场桥配比时的结果进行了分析,以此来验证所提出模型的优越性。
4.1 参数设定
针对两种情况下的实验1与实验2的模型参数采用相同的设置(详见表1~3)。其中,表1 为集装箱码头的各设备实验参数,岸桥处理一个集装箱任务的时间为50 s,场桥处理一个集装箱任务的时间为55 s,AGV 行驶的速度为5 m/s;表2 为各集装箱任务的目标堆场箱区;表3为岸桥到各箱区的距离。

表1 集装箱码头设备试验参数

表2 集装箱目标堆场
4.2 结果分析
(1)未考虑避碰规则情况下
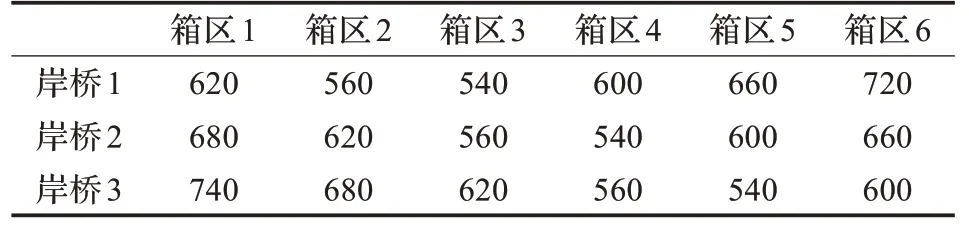
表3 岸桥与各箱区的距离 m
分别考虑了11 种不同参数设置下的实验:算例1~3考虑了卸箱数量均为60、岸桥均为3、箱区均为6 情况下,AGV 数量分别为12、15、18 的情况;算例4~6 跟算例1 保持相同的岸桥-AGV-场桥配比情况下分别将卸箱数量增加为80、120、180 的情况;算例7、8 跟算例2 保持相同的岸桥-AGV-场桥配比情况下分别将卸箱数量增加为250、330的情况;算例9~11跟算例3保持相同的岸桥-AGV-场桥配比情况下分别将卸箱数量增加为420、550、700 的情况。实验结果如表4 所示,可以看出在相同卸箱数量情况下,AGV 数量越多,总任务完成的时间越少;在岸桥、AGV、箱区数量相同的情况下,卸箱数量越多,总任务完成时间越长。

表4 未考虑避碰下的实验结果
以算例1为例,可得AGV的最优调度方案如下:
AGV1 的调度方案为(2,37)→6,(1,4)→1,(1,49)→1,(3,43)→3,(3,10)→2
AGV2 的调度方案为(3,28)→1,(2,59)→6,(1,55)→6,(1,44)→4,(3,51)→5
AGV3 的调度方案为(1,11)→4,(3,13)→5,(3,53)→4,(2,39)→2,(1,31)→6
AGV4 的调度方案为(3,47)→2,(2,48)→3,(2,5)→5,(3,8)→6,(2,24)→4
AGV5 的调度方案为(2,30)→3,(3,29)→2,(2,57)→3,(1,45)→1,(1,32)→1
AGV6 的调度方案为(1,20)→5,(1,23)→4,(3,15)→2,(2,34)→5,(2,22)→2
AGV7 的调度方案为(3,50)→1,(2,16)→4,(2,26)→4,(2,12)→5,(1,3)→3
AGV8 的调度方案为(1,17)→4,(3,56)→5,(1,40)→3,(3,38)→6,(2,7)→3
AGV9 的调度方案为(2,14)→6,(1,21)→6,(2,36)→6,(2,25)→1,(1,60)→5
AGV10 的调度方案为(2,52)→2,(2,58)→3,(3,33)→2,(1,18)→2,(3,2)→1
AGV11 的调度方案为(3,41)→3,(1,42)→1,(3,46)→1,(3,35)→3,(2,54)→4
AGV12 的调度方案为(1,19)→5,(3,27)→2,(1,9)→5,(1,6)→4,(3,1)→6
以AGV1 为例,代表含义为AGV1 执行岸桥2 的37号集装箱任务到达箱区6,执行岸桥1的4号集装箱任务到达箱区1,执行岸桥1 的49 号集装箱任务到达箱区1,执行岸桥3 的43 号集装箱任务到达箱区3,执行岸桥3的10号集装箱到达箱区2。
图3 为算例1 集装箱任务调度结果的甘特图,绿色表示岸桥处理时间,红色代表AGV 的碰撞时间,蓝色代表AGV 处理集装箱任务的时间(包括返回时间),橙色代表场桥处理的时间。从图3 中可以明显地看到AGV存在碰撞的时间。

图3 集装箱调度结果甘特图(未考虑避碰规则)
在AGV 进行任务作业时,会发生碰撞,下面就卸箱数量均为60,岸桥-AGV-箱区的作业情况下,各AGV 之间的路口碰撞情况进行说明。如图4 与图5 所示,在任务进行至209 s时,4号AGV和10号AGV在路口发生冲突,10 号AGV 等待1 s,此时,5 号AGV 和11 号AGV 在路口发生冲突,11 号AGV 等待1 s,由于两辆AGV 在路口发生冲突,必有一辆AGV 要等待,才能使另一方顺利通过,增加了总任务的完成时间。如图6,在任务进行至221 s时,6号AGV 和12号AGV 发生碰撞,12号AGV 等待1 s,使6号AGV顺利通过,增加了总任务的完成时间。
(2)考虑避碰规则情况下
在考虑避碰规则的情况下,采取了与不考虑避碰规则相同的设置下的11 个算例进行比较分析。实验结果如表5所示。
下面举例就卸箱任务数量为60,岸桥-AGV-场桥配比为3-12-6的运行情况进行说明。

图4 AGV4与AGV10离碰撞路口距离图

图5 AGV5与AGV11碰撞路口距离图

图6 AGV6与AGV12碰撞路口距离图

表5 考虑避碰规则下的实验结果
AGV1 首先在岸桥下等待就绪,岸桥开始AGV1 首次运送37 号任务至6 号场桥,AGV2 运送28 号任务至1号场桥,AGV3 运送11 号任务至4 号场桥;AGV4 运送47 号任务至2 号场桥,AGV5 运送30 号任务至3 号场桥,AGV6 运送20 号任务至5 号场桥;AGV7 运送50 号任务至1 号场桥,AGV8 运送17 号任务至4 号场桥,AGV9运送14号任务至6号场桥。
AGV2 将任务送至目标箱区,判断下一任务为2 号岸桥的59 号任务优先级最高,AGV2 从1 号场桥返回至2 号岸桥取59 号任务,AGV3 从4 号场桥返回至3 号岸桥取13 号任务,AGV1 从6 号场桥返回至1 号岸桥取4 号任务。
AGV10 从岸桥2 出发运送52 号任务至2 号场桥,AGV11 从岸桥3 出发运送41 号任务至3 号场桥,AGV12从岸桥1出发运送19号任务至5号场桥。
AGV4从2号场桥返回至2号岸桥取任务,AGV5从3号场桥返回至3岸桥取任务,AGV6从5号场桥返回至1号岸桥取任务。
在AGV10 从岸桥2 至场桥2 运送任务,AGV4 从场桥2 返回过程中,在如图7 位置点b1 发生冲突。若在考虑避碰规则后,则节约本次等待时间。

图7 冲突位置图
此外,从实验结果可知当卸箱数量相同时(算例1,2,3),随着AGV 数量增多,总任务完成时间减少;当岸桥、AGV、场桥数量相同时(算例4,5,6),随着卸箱数量增多时,总任务完成时间增加。
在任务进行至第209 s 时,4 号和10 号AGV 发生碰撞,此时10 号AGV 处于如图8 的8 号相位,4 号AGV 处于如图8 的3 号相位,由于避碰规则的设置,8 号相位与3号相位属于相容相位,可以顺利通过,节约了在路口的等待时间;5 号和11 号AGV 发生碰撞,同样,此时11 号AGV处于如图8的8号相位,5号AGV处于如图8的3号相位,由于避碰规则的设置,8号相位与3号相位属于相容相位,可以顺利通过,节约了在路口的等待时间。

图8 AGV4与AGV10、AGV5与AGV11路口相位图
任务进行至221 s 时,6 号和12 号AGV 发生碰撞,此时12 号AGV 处于如图9 的7 号相位,6 号AGV 处于如图9 的5 号相位,为相冲突的相位,12 号AGV 仍需等待1 s。

图9 AGV6与AGV12路口相位图
图10 为考虑避碰规则情况下算例1 集装箱任务调度结果的甘特图,绿色表示岸桥处理时间,红色代表AGV 的碰撞时间,蓝色代表AGV 处理集装箱任务的时间(包括返回时间),橙色代表场桥处理的时间。由图可见,在考虑避碰规则情况下的碰撞等待时间减少。

图10 集装箱调度结果甘特图(考虑避碰规则)
4.3 实验结果比较
为了更直观地看出模型的优越性,对相同卸箱数量、不同AGV 数量以及相同AGV 数量、不同卸箱数量在考虑与未考虑避碰规则的情况下进行了比较。
岸桥数量为3,场桥数量为6,固定卸箱数量为60,AGV数量分别为12、15、18下的未考虑避碰规则和考虑避碰规则的对比图如图11。可以看出,未考虑避碰规则的总任务完成时间多于考虑避碰规则的总任务完成时间。
岸桥-AGV-场桥数量固定为3-15-6 情况下,箱区数量为60、250、330 时考虑避碰规则和未考虑避碰规则下的对比结果如图12 所示。同样可以看出,未考虑避碰规则的总任务完成时间多于考虑避碰规则的总任务完成时间。
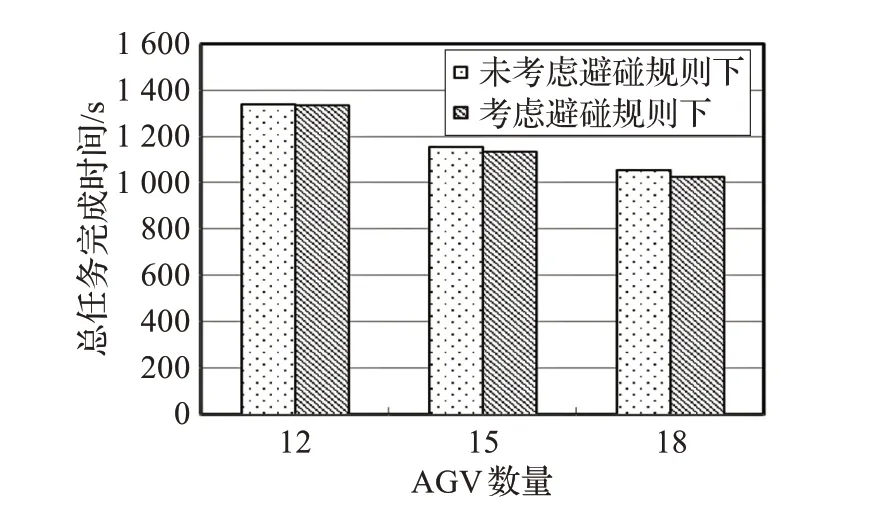
图11 AGV数量不同、卸箱任务相同情况下的对比

图12 AGV数量相同、卸箱任务不同情况下的对比
同时,如图13 与图14 所示,分别卸箱数量为60,岸桥、箱区数量为3和6情况下不同AGV 数量的碰撞耗时图与岸桥-AGV-箱区数量为3-15-6,不同卸箱数量的碰撞耗时图。实验结果表明,在卸箱数量,AGV 数量增多情况下,发生碰撞的几率就越大,在考虑设置的避碰之后,节约了AGV在路口的等待时间,从而使调度结果更优化。

图13 卸箱任务相同、AGV数量不同碰撞耗时图

图14 AGV数量相同、卸箱任务不同碰撞耗时图
在11 个算例中,考虑避碰规则后平均任务完成总时间减少率如表6 所示,提升了整个卸船作业流程的效率,算例结果表明,考虑避碰规则下的解要优于未考虑避碰规则下的解。

表6 考虑避碰规则后总任务完成时间减少率
通过上述分析最终能得出以下结论:
(1)在AGV 数量、岸桥和箱区数量一致时,随着卸箱任务增多,AGV 碰撞等待时间越长,即发生冲突概率增加,总任务时间增加。
(2)在卸箱数量、岸桥和箱区数量一致时,AGV 数量增多,AGV 碰撞等待时间越长,发生冲突概率增加,总任务时间增加。
(3)考虑避碰规则下的碰撞耗时明显少于不考虑避碰规则下的耗时。
(4)考虑避碰规则下总任务完成时间小于不考虑避碰规则下的总任务完成时间。
(5)考虑避碰规则的总的码头操作效率明显高于不考虑避碰的情况。
5 结束语
本文针对AGV 小车路口碰撞问题,考虑任务分配、路口避碰等约束,建立以最大完工时间最小化为目标的自动化集装箱码头协同调度模型。并对任务数量、岸桥、AGV、箱区数量进行不同配比情况下的模型进行验证和比较。实验结果表明在考虑AGV 避碰规则之后,平均任务总完成时间减少。
但本文只考虑了路口的碰撞问题,其他碰撞问题还有待深入研究。另外,实际情况下,不同的集装箱在不同堆场的存放顺序也对总任务处理时间有影响,未来的研究可考虑在装卸并行的情况下,考虑集装箱在堆场的存放顺序等因素,使其更符合集装箱码头的实际情况。

