一类具有饱和发生率和恢复率的生态流行病模型
冯宇星,雒志学,胡永亮,梁丽宇
(兰州交通大学 数理学院,兰州 730070)
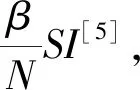
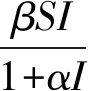
1 模型的建立
建立具有饱和发生率、恢复率和HollingⅡ功能反应函数的生态流行病模型:
(1)
其中:S表示易感食饵;I表示染病食饵;Y表示捕食者;r表示内禀增长率;k表示环境容纳量;β表示传染率系数;α是抑制系数;γ表示庇护系数;c1,c2分别表示捕食者对染病食饵和易感食饵的捕食率系数;d1,d2分别表示染病食饵和捕食者的死亡率;δ表示染病食饵的恢复率;e(0 证明:定义函数N(t) N(t)=S(t)+I(t)+Y(t). 该方程沿系统(1)的解关于时间t的导数是 即: 由于 0 故 定义方程 当t>T时,由比较定理得 通过解下面方程组: 易求得系统(1)有以下平衡点: 定理3.1系统(1)的零平衡点E0不稳定. 证明:系统(1)的线性化系统在点E0处的Jaccobi矩阵为 对于零平衡点E0,其Jaccobi矩阵的特征方程为 (λ-r)(λ+d1+δ)(λ+d2)=0. 显然,该特征方程存在两个负实根和一个正实根,故E0是一个鞍点,且不稳定. 证明:系统(1)的线性化系统在边界平衡点EK处的Jaccobi矩阵为 对于边界平衡点EK,其Jaccobi矩阵的特征方程为 由此可得特征根为 当R0<1,R1<1时,边界平衡点EK将局部渐近稳定,而当R0>1或R1>1时,边界平衡点EK不稳定. 定理3.3当R0<1,R1<1时,边界平衡点EK全局渐近稳定. 证明:构造Liapunov函数V=eI+Y沿着系统(1)的轨线关于t求导得 且系统(1)在E中存在最大的不变集M=E={I=0,Y=0}再由LaSalle不变集原理可知,对于系统(1)的一切解均有 证明:模型(1)的线性化系统在点E*处的Jaccobi矩阵为 对于无病平衡点E*,其Jaccobi矩阵的特征方程为 证明:构造Liapunov函数V=I沿着系统(1)的轨线关于t求导得 (2) 令t=(m+(1-γ)S)τ,则系统(2)化为 取Dulac函数B(S,Y)=S-1Yn-1,则有 现在只需要证明存在实数n,使得φ(S,n)≤0即Δ<0,即 再令 (λ-a33)(λ2-(a11+a22)λ+a11a22-a12a21)=0, 下面证明该平衡点的全局渐进稳定性. 构造Liapunov函数V=Y沿着系统(1)的轨线关于t求导得 (3) 则 证明:考虑平均Liapunov函数V(S,I,Y)=Sα1Iα2Yα3(α1,α2,α3>0)则2 系统解的有界性
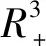
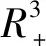

3 平衡点的存在性和稳定性
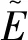




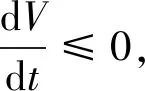
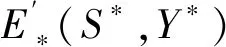
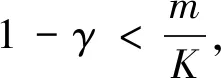

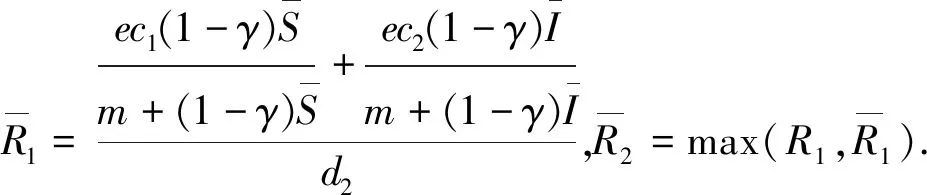



4 系统的一致续存