和圆有关的存在性问题的主要求解方法

雷亚庆

(江苏省南京市大厂高级中学 210044)

和圆有关的存在性问题主要有两种处理方法，一是从代数角度把问题转化为方程组有解的问题，二是从几何角度利用位置关系求解.本文来介绍一下利用位置关系如何解决这类存在性问题.

一、转化为圆与其他曲线的位置关系

1.直线与圆

例1在平面直角坐标系xOy中，已知圆x2+y2=4上有且仅有四个点到直线12x-5y+c=0的距离为1，则实数c的取值范围是____.

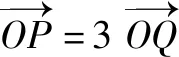
2.圆与圆

例3圆(x-a)2+(y-a)2=4上总存在两个点到原点的距离为1，则实数a的取值范围是____.

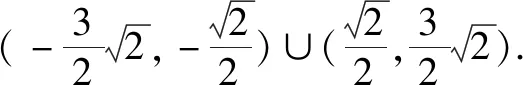
例4在平面直角坐标系xOy中，若圆C1:x2+(y-1)2=r(r>0)上存在点P，且点P关于直线x-y=0的对称点Q在圆C2:(x-2)2+(y-1)2=1上，则r的取值范围是____．(苏北四市2018一模)

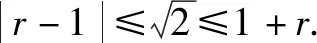
3.圆与椭圆

解析连接OA，OB，OP，依题意，O、P、A、B四点共圆.

∵∠APB=60°，∴∠APO=∠BPO=30°，

图1

二、利用临界角

图2

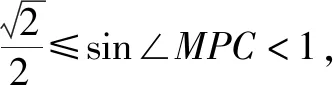
所以4<(x0-3)2+(2x0-0)2≤8.

图3

例8已知圆C：(x+1)2+(y+1)2=1，点P(x0，y0)在直线x-y+2=0上．若圆C上存在点A使∠CPA=30°，则x0的取值范围是____.

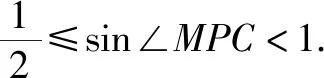
解得x0的取值范围是[-3,-1].

三、利用临界距离

解得-7≤m≤-1或7≤m≤13.

由①②得实数m的取值范围是[-7,1]∪[5,13].