板块模型题解法例析

胡连冬

(湖南省宁乡市第七高级中学 410635)

板块模型是依靠摩擦相互作用的木板和木块发生相对运动的问题.这类问题涉及受力分析和运动情况分析、牛顿运动定律和能量守恒定律.分析板块问题有以下四种基本方法.

一、运动过程图示法

例1如图1所示质量为M的长木板静止在光滑的水平地面上，在长木板的左端有质量为m的小木块以初速v0沿水平向右的方向滑动，木块和木块之间的动摩擦因数为u，木块可看作质点，求木块刚好不滑离木板时，木板的长度至少为多少？

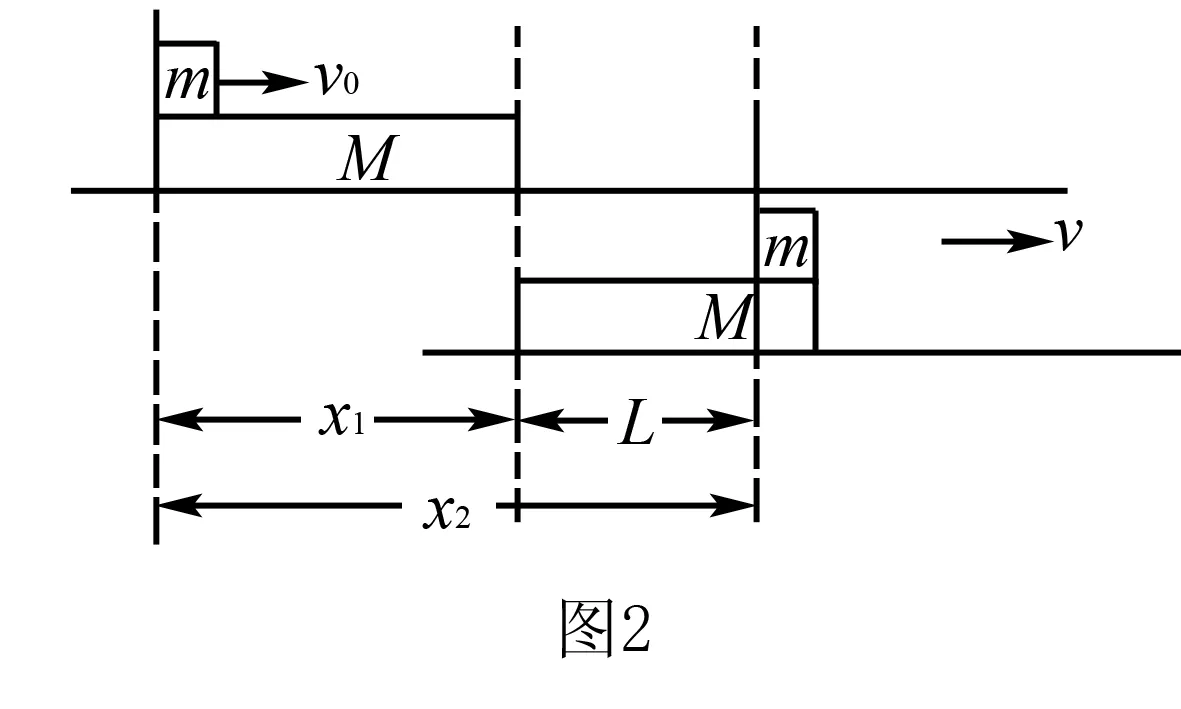
析与解当木块运动到木板右端，且两者速度相同时，木块刚好不滑离木板，运动过程如图2所示. 设木块运动方向为正方向，木块、木板的加速度为a1、a2，它们速度相同时经历的时间为t.由牛顿第二定律得：

umg=ma1①，umg=Ma2②

当木块、木板速度相同时，有：v0-a1t=a2t③

根据运动学公式，木板、木块在t时间内发的位移分别为：

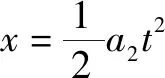
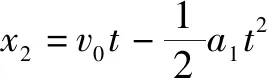
由图2可知木板的最小长度为：l=x2-x1⑥

二、速度图像法

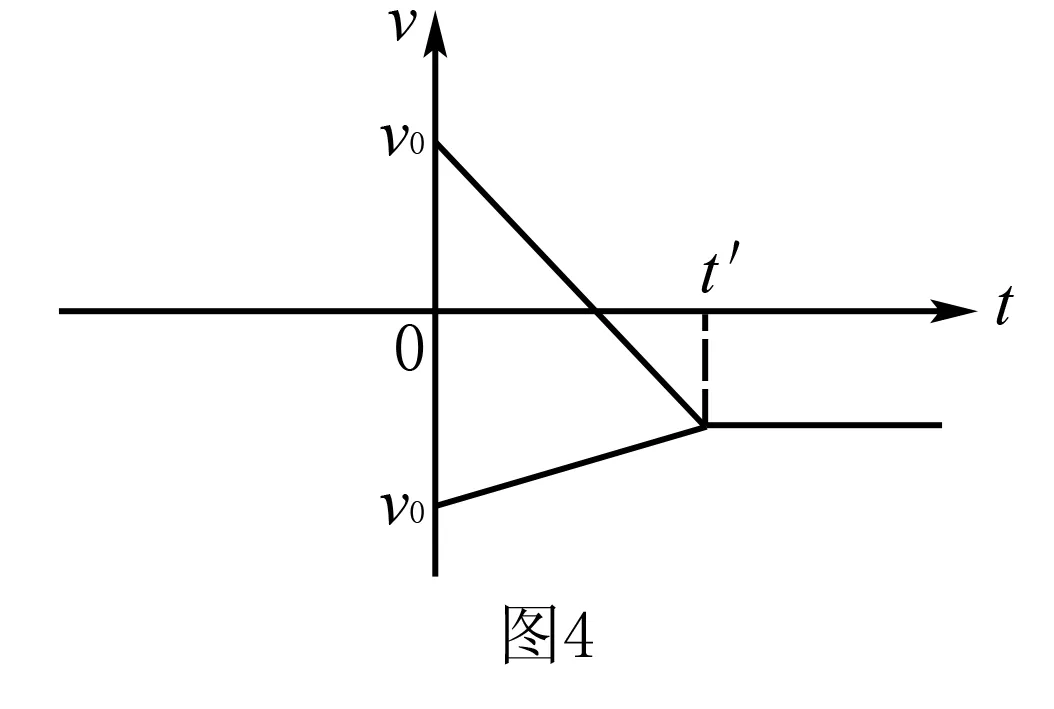
例2如图3所示，若在例1中，木板木块同时具有大小相等方向相反的初速V0，木板的质量M大于木块质量m，当木块刚好不滑离木板时，木板的最小长度是多少？

析与解以木块的初速方向为正方向，由受力分析可知，木块、木板都做匀变速直线运动，当两者速度相同时，木块刚好到达木板右端.设木块、木板的加速度分别为a1、a2，根据牛顿第二定律得：

umg=ma1①umg=Ma2②

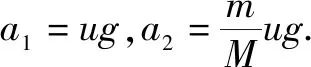
速度的时间为t′，则V0-a1t′=-V0+a2t′ ③

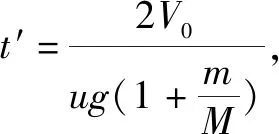
三、相对运动法

例3在例2中，如果地面粗糙，其动摩擦因素也为u，且木板质量是木块质量的2倍，其他条件不变.求木块不滑离木板时，木板的最小长度.

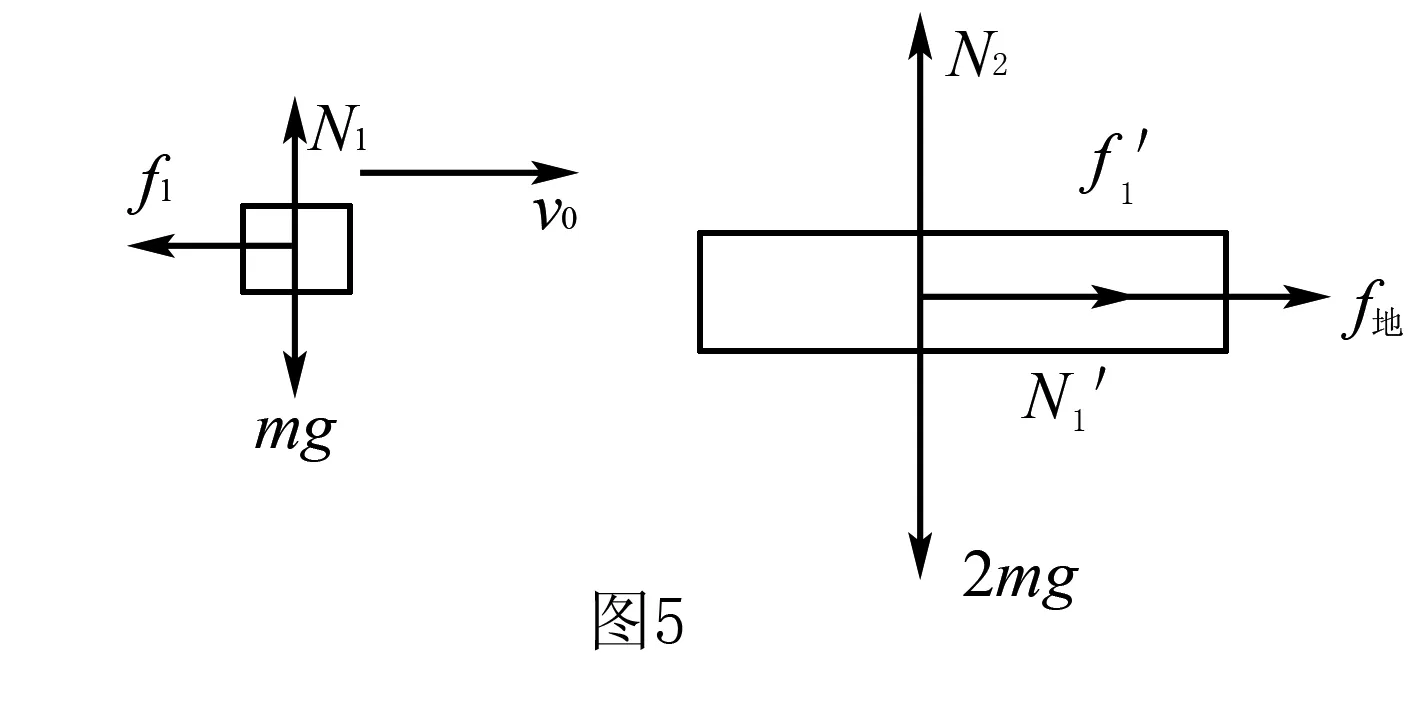
析与解仍以木块初速方向为正方向，设木块质量为m，则木板质量为2m，如图5所示，隔离木块、木板画受力分析图.

木块受摩擦力：f1=umg

木板受木块及地面的摩擦力分别为：

f1′=umg，f地=3umg

木板所受摩擦力的合力为f2=4umg，由牛顿第二定律可知，木块、木板的加速度分别为：a1=ug，a2=2μg

由上例分析知：f2=4umg②

此时木块的加速度和速度分别为：

a1=-ug③v1=v0-a1t④

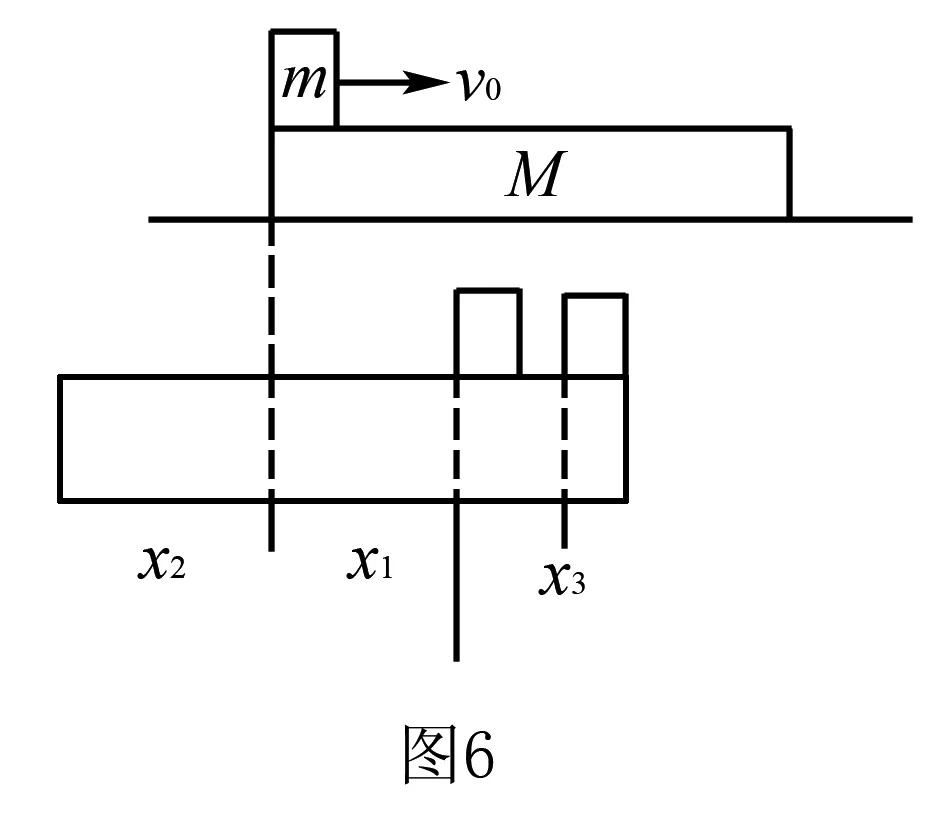
当木板静止时它们对地的位移分别为x1、x2，如图6所示，对木块、木板分别运用能量守恒定律得：

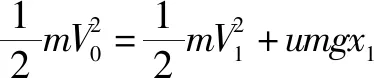
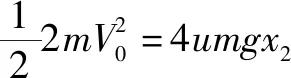
木块相对木板的位移：Δx=x1+x2⑧