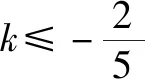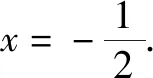“数形结合”思想在高中数学中的应用
蔺兴旺
(甘肃省张掖市山丹第一中学 734100)
数学这门学科的学习在学生的学习生涯中的重要性不言而喻,并且数学不仅是学生学习的重要学科,也是促进科学发展、促进社会进步的重要学科.而数学的主要研究方向就是数量关系和空间形式,说白了就是主要研究数、形的一门学科.因此,在高中数学中,灵活地运用数形结合思想是学好数学所必要的.但是,由于高中学生受到思维方式和生活经验的限制,数形结合的思想还不能很好地灵活运用.所以,高中数学教师就有必要重视数形结合思想解题方法的教学了.笔者总结了一些高中数学中运用数形结合思想的解题方法,涵盖了高中数学中大部分要运用数形结合思想来解题的题型.
一、数形结合思想概论
数学的起源就是古人研究的数形关系,数和形是数学研究的基本对象,其在某些条件下可以互相的转换.在高中数学中,也是研究数形的关系,而数形结合就是数与形的关联.数形结合是一种数学思想,其有两种模式:一是使用数来阐述形的特点和属性,二是使用形来直观地表示数之间的关系.
笔者总结了在高中数学中运用数学思想的解题方法主要在三个方面:1.运用数形结合思想解决函数问题.2.运用数形结合方法解决不等式问题.3.运用数形结合解决平面几何问题.前两种都是用形来直观表示数之间关系的数形结合思想,第三种是使用数来阐述形的属性特点.
这些题型包含了高中数学中的大量题型,相信如果掌握了这些数形结合的思想方法并且灵活的运用,就能够提高数学的成绩.所以,教师要在日常教学中贯穿这些数形结合思想方法的教学,因为这些数形结合思想对学生的数学学习很有帮助.下面,笔者就结合一些例题来演示这些数形结合思想的解题方法.
二、数形结合思想解决函数问题
数形结合思想在函数问题中的运用很广泛,比如在函数的最值、值域、取值范围问题上,函数的单调性、奇偶性上,甚至在函数的概念性问题上都有运用.
例题1(函数的概念问题)下列选项中,哪个选项的函数存在反函数.
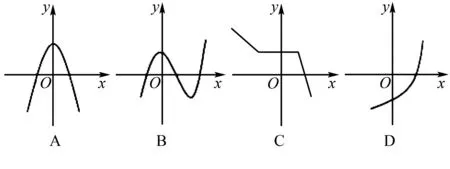
这个问题可以由反函数的定义得出答案:
由此可以得到有反函数的函数在“形”上的特点是x与y只能一一对应,所以此题应当选D选项.
例题2(函数取值范围问题)设函数y=x2+2ax+1在(+∞,1]上为减函数,求a的取值范围.
对于此类问题应当运用数形结合思想来解答:
由函数解析式可得函数图象的对称轴为x=-a.
∵此函数在(+∞,1]上单调递减.
∴由函数图象特征可得对称轴x=-a必须在直线x=1上或者在直线x=1的右侧,有-a≥1.
∴得到a≤-1.
例题3(函数单调性、奇偶性问题)设奇函数f(x)在[3,7]上单调递增,并且函数在此区间上的最小值为6,求此函数在区间[-7,-3]上的单调性以及最大值.
这个问题可以通过函数特征结合图象来解答:
∵f(x)为奇函数,
∴f(x)的图象关于原点O对称.
∵f(x)在[3,7]上单调递增,在此区间上最小值为6,
∴f(x)在[-7,-3]单调递增,并且最大值为-6.
三、数形结合思想解决不等式问题
在不等式问题中运用数形结合思想来解答,可以避免复杂的分类讨论,简化题目,直接利用几何图形特点得出答案.
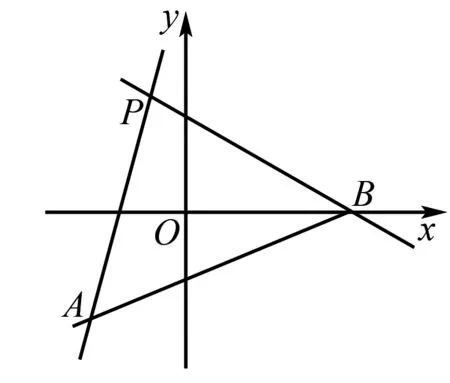
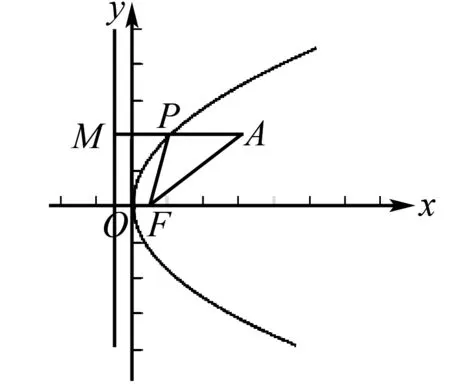
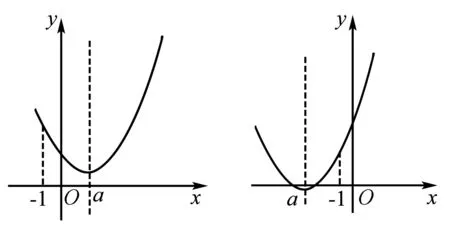
例题4 设有关于x的不等式|x-3|+|x-4| 解设函数f(x)=|x-3|+|x-4|,函数g(x)=a,在平面直角坐标系中作出函数f(x)和g(x)的图象如下. 由函数f(x)和g(x)的图象特征可得要使|x-3|+|x-4| 所以可得a的取值范围为(-∞,1]. 例题5设函数f(x)=x2-2ax+2, 并且x∈[-1,+∞)时,f(x)≥a恒成立,求a的取值范围. 对于此题有两种解法: 解法1由当x∈[-1,+∞)时,f(x)≥a恒成立可得x2-2ax+2-a≥0在x∈[-1,+∞)时恒成立. 所以题目可以化为求a的取值范围使得函数g(x)=x2-2ax+2-a的图象在区间[-1,+∞)位于x轴上方.作出图象,有如下两种情况: 由图象可得不等式的成立条件是: (1)Δ=4a2-4(2-a)<0⟹a∈(-2,1). 综上所述a的取值范围是(-3,1). 解法2由f(x)≥a可得x2-2ax+2≥a即x2+2>a(2x+1). 设函数f(x)=x2+2,函数g(x)=a(2x+1),作出函数f(x)和函数g(x)的图象. 由函数图象特征可得a的取值范围为图中直线斜率的取值范围. 即a的取值范围是(-3,1). 在高中数学中,平面解析几何知识是运用到数形结合思想最广泛的知识点,在直线斜率、直线与圆、直线与圆锥曲线等问题上,运用数形结合思想解题是最为简捷的. 例题6 (直线斜率问题)直线l过点P(-1,2),且与点A(-2,-3)、B(4,0)为端点的线段AB相交,求直线l的斜率的取值范围. 在解这类题目时,先作出直线PA、PB,线段AB. 例题7 (直线与圆问题)设圆O的方程为x2+y2-2x+4y+4=0,直线l的方程为3x-4y+9=0,求圆O上的点P到直线l上的最大距离为多少. 在解这类问题时,运用数形结合思想能使问题得到迅速解决. 将圆的方程配方可得(x-1)2+(y+2)2=1,由此可得圆心O为(1,-2),半径r=1. 由直线与圆的图形特征可得:圆到直线的最大距离=圆心到直线的距离+半径. 圆心O到直线l的距离d=4.由上式可得点P到直线l的最大距离为d+r=4+1=5. 例题8(直线与圆锥曲线问题)设点P是抛物线y2=2x上的动点,F是此抛物线的焦点,设点A(3,2),求|PA|+|PF|的最小值. 对于这个问题,先画出抛物线和准线. 由抛物线的定义可得PF=PM,所以|PA|+|PF|=|PA|+|PM|. 总而言之,数形结合思想在高中数学的学习中对学生是非常有帮助的,其在高中数学中的运用非常广泛,比如在函数问题、不等式问题、平面解析几何中都有非常广泛的运用.运用数形结合思想来解这些题目可以非常简捷迅速地得出答案.学生如果掌握和运用好了数形结合思想,就能更加轻松地学习数学,提高考试成绩.所以,高中数学教师在日常的教学中要始终贯穿数形结合思想的教学,让学生掌握好这一数学思想并且灵活地运用.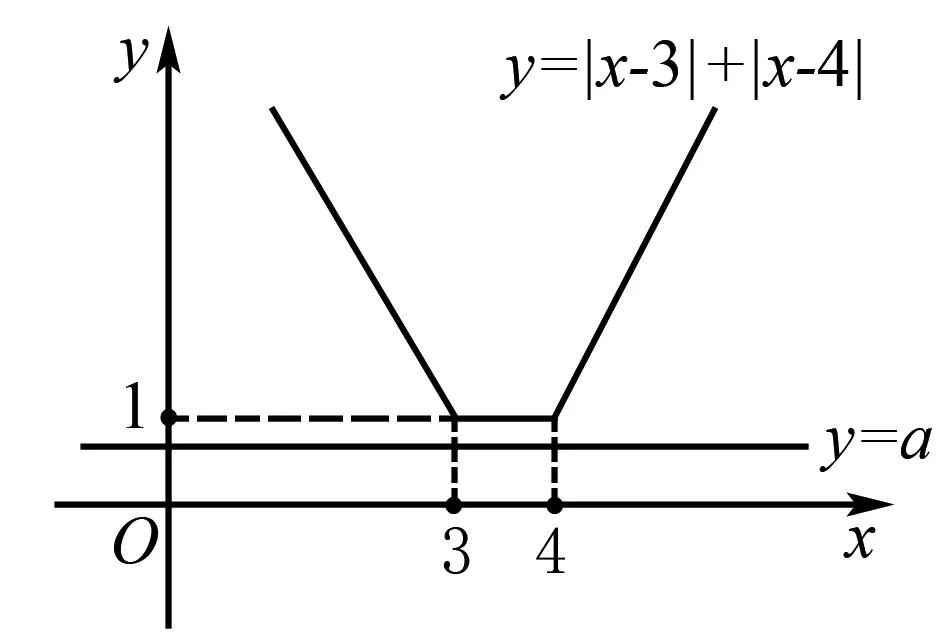

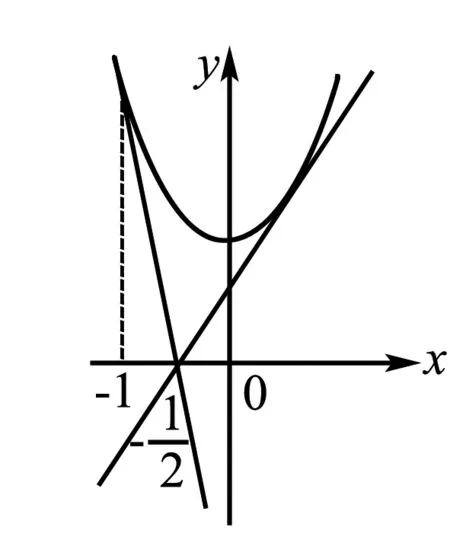
四、数形结合思想解决平面解析几何问题