最高点即是临界

黄兴仲

(广东省梅州市丰顺县黄金中学 514357)

竖直平面内的圆周运动，作为高中常见的运动类型，在复习时，通常会介绍两个一般模型：绳——球模型与杆——球模型.小球要刚好做完整的圆周运动，前者的临界条件为到达最高点时，小球的重力恰好提供向心力，后者为杆对小球的支持力恰好等于重力.

一、最高点为临界状态的原因

以绳——球模型为例，当小球从最低点以较大的速度运动时，则要做完整的圆周运动，必然要达到最高点，而从最高点运动下去时(如图1)，由于A、B两点位于同一高度，因而由对称性可知，此时小球若能达到A点，也即是可到达B点，即是说明只要小球能够通过最高点，则说明小球能做完整的圆周运动.

然而一旦加上一些外在条件的限制，最高点则未必就是临界状态.

二、绳子的拉力有限制

当绳子的拉力有限制时，绳子对小球的拉力的最大值出现在下半圆中，此时最高点则不是所需要的临界状态.

假设绳子拉力存在上限值Tm时，对小球进行受力分析(如图2)，在径向上：

假设最高点的速度为v0，则从最高点到最低点，由动能定理得

由以上两式联立可得

若α=0°即最低点时，此时绳子的拉力达到最大为

例1一根长度为l的轻绳，一端固定在某点O，另一端系一个质量为m的小球.若小球恰好过最高点，而轻绳所能承受的最大拉力为6mg.则小球下落过程中将在何处轻绳被拉断？

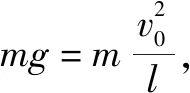
三、考虑竖直分力

在某些特殊的情景中，需要考虑弹力的竖直分力问题，如常见的竖直平面内的圆周运动与底座的问题.

例2 质量为M的支架(包含底座)上有一水平细轴，轴上套有一长为L的轻质细线，绳的另一端拴一质量为m(可视为质点)的小球，如图3.现使小球在竖直面内做圆周运动，已知小球在运动过程中底座恰好不离开地面、且始终保持静止.忽略一切阻力，重力加速度为g.则( ) .

A.小球运动到最高点时底座对地压力最大

B.小球运动过程中地面对底座始终无摩擦力

C.小球运动至右边与O点等高时，地面对底座的摩擦力向左

D.小球运动到最高点时细线拉力大小为Mg

答案：CD

其解析在最高点时，细线对小球的竖直拉力达到最大，即在此时底座的压力达到最小，结合本题可知此时压力为0，因而A错误D正确；当小球不在竖直线时，细线对底座的拉力在水平方向上有分力，由于底座始终静止，所以地面对底座有摩擦力作用，当小球运动至右边与O点等高时，细线对底座的拉力水平向右，故地面对底座的摩擦力水平向左，因而B错误C正确.

分析在此题中，只是想当然地认为圆周运动中圆轨道的最高点就是竖直分力最大的位置，但实际不一定是这样，以下为证明过程：

如图4，假设细线与竖直方向夹角为α时，小球速度为v，则

假设小球在最低点的速度为v0，则从最低点到A点的过程中，由动能定理得

联立以上两式，可得

其竖直分量为

当α∈(0°,90°]时，小球不在最高点，但此时Ty最大，此时需要满足的条件为

四、外加匀强电场

此类题型的解法往往采用等效重力法，将重力场中竖直圆周运动中的临界问题类比到等效重力场中，从而更好实现问题的解决.

例3 如图5所示，一条长为L的细线上端固定，下端拴一个质量为m的电荷量为q的小球，将它置于方向水平向右的匀强电场中，使细线竖直拉直时将小球从A点静止释放，当细线离开竖直位置偏角α=60°时，小球速度为0.求：

(1)电场强度E.

(2)若小球恰好完成竖直圆周运动，求从A点释放小球时应有的初速度vA的大小(可含根式).

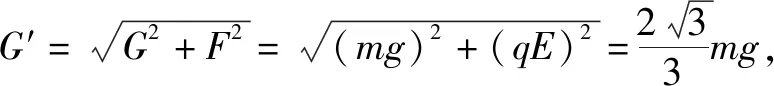
从最高点到最低点，由动能定理得：

五、脱轨问题

圆周运动中物体不脱离轨道，可分为以下情况：

1.内轨运动

(1)在圆心水平面下方：此时的临界条件为最高点时由重力提供向心力和恰好到达圆心等高处；

(2)在圆心水平面上方：轨道对物体的弹力恰好为0；

2.外轨运动

(1)顶端下滑：此时的临界条件为最高点时由重力提供向心力和轨道对物体的弹力为0；

(2)顶端上滑：此时的临界条件为在起抛点轨道对物体的弹力恰好为0 .

例4如图6所示，轮半径r=40 cm的传送带，水平部分AB的长度L=1.5 m，与一圆心在O点半径R=1 m的竖直光滑圆轨道的末端相切于A点，AB高出水平地面H=1.25 m.一质量m=0.1 kg的小滑块(可视为质点)，由圆轨道上的P点从静止释放，OP与竖直线的夹角θ=37°.已知sin37°=0.6，cos37°=0.8，g=10 m/s2，滑块与传送带的动摩擦因数μ=0.1，不计空气阻力.

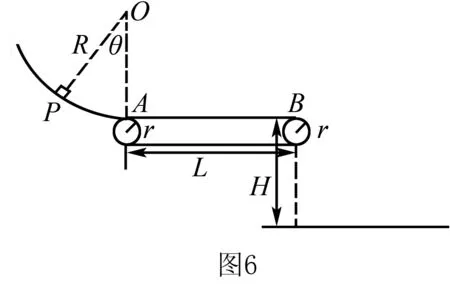
(1)求滑块对圆轨道末端的压力.

(2)若传送带一直保持静止，求滑块的落地点与B间的水平距离.

解(1)略.

(2)从A到B，根据动能定理得：

其中第(1)问中求得vA=2 m/s

代入数据解得vB=1 m/s

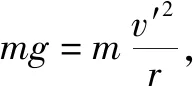
从B点到C点，由动能定理得

从C点脱离后，在水平方向上x=vCcosα·t

在竖直方向上

联立以上各式，代入数据即可解得(因数据过大，此处不做详解).