缩小参数范围 减少讨论环节

李秀元 朱丹丹

(湖北省武穴市实验高级中学 435400)

利用导数研究函数的综合问题，是高考的必考考点.其中，利用恒成立求参数取值范围是重点，也是难点.求解过程中如果不能直接分离参数与变量，学生往往很难把握分类标准，解题时漏洞百出，失分较严重.如果能适当缩小参数的取值范围，那么讨论起来会简单些.下面通过几道例题，来说明如何利用题目恒成立的不等式条件，用特殊自变量的值来缩小参数取值范围，使求解方向更明确，解题过程更简捷，从而节省考试时间，提高得分率.

例1 已知函数f(x)=x2+ax-lnx，x∈R.

(1)若a=0，求曲线y=f(x)在点(1，f(1))处的切线方程；

(2)若函数f(x)在[1，2]上是减函数，求实数a的取值范围；

(3)令g(x)=f(x)-x2，是否存在实数a，当x∈(0，e](e是自然对数的底数)时，函数g(x)的最小值是3？若存在，求出a的值；若不存在，请说明理由.

解析(1)过程略，切线方程为y=x.

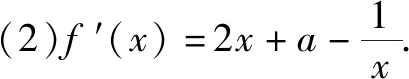
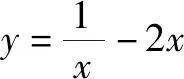
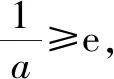
综合可知，a=e2.

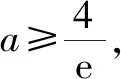
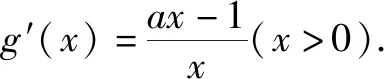
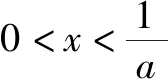
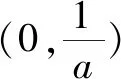
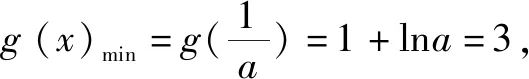
即当a=e2时，函数g(x)在(0，e]上的最小值为3.

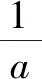
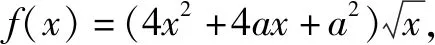
(1)当a=-4时，求f(x)的单调递增区间；

(2)若f(x)在区间[1，4]上的最小值为8，求a的值.

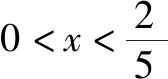
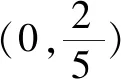
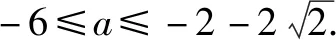
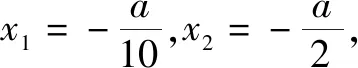
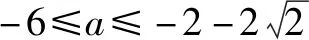
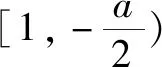
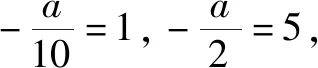
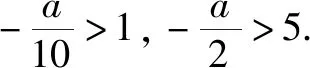
综上得a=-10.

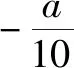
例3 设函数f(x)=x2+ax+b，g(x)=ex(cx+d).若曲线y=f(x)和曲线y=g(x)都过点P(0，2)，且在点P处有相同的切线y=4x+2.

(1)求a，b，c，d的值；

(2)若x≥-2时，f(x)≤kg(x)恒成立，求k的取值范围.

解析(1)a=4，b=2，c=2，d=2.

(2)由(1)知，f(x)=x2+4x+2，g(x)=2ex(x+1).

设F(x)=kg(x)-f(x)=2kex(x+1)-x2-4x-2，则“f(x)≤kg(x)”等价于“F(x)≥0对x≥-2恒成立”，即“对任意的x≥-2，F(x)min≥0”.

依题意，必有F(-2)≥0且F(0)≥0，所以1≤k≤e2.

因为F′(x)=2(x+2)(kex-1)，令F′(x)=0，得x1=-lnk，x2=-2.

当1≤k0得x>x1.所以F(x)为(-2，x1)上的减函数，(x1，+)上的增函数.

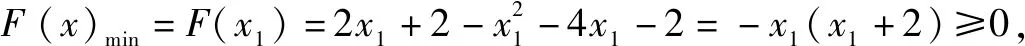
当k=e2时，F′(x)=2(x+2)(ex+2-1)≥0，所以，F(x)为[-2，+)上的增函数，故F(x)min=F(2)=0，也符合题意.

综合可得，1≤k≤e2.

点评由于g(x)的取值有正有负，因此分离参数法不太方便.如果不用特殊值缩小参数的范围，势必需要增加讨论k≤0、0e，过程虽不难，但增大了书写量.若只选择一个特殊值，如x=-2，参数范围虽有缩小，但还不是更小，更多的讨论依然避免不了，因此我们选择定义域内的两个特殊值，使参数范围更小.

纵观这几道试题，我们发现解决问题的关键是利用了恒成立问题的必要条件，以缩小参数的取值范围.在自变量的取值范围内，究竟选谁作为特殊值，是选一个还是多个，是没有规定的.一般情况下，区间端点、中点、整点，或者使函数式为定值的自变量等等都是我们考虑的对象，选出特殊值，经过简单计算，择其优而用之. 通过缩小参数的取值范围，我们只是尽可能多地减少解题过程中的讨论环节，避免不必要的麻烦.但在具体讨论过程中，一些细节依然要引起重视，如后两例中对参数范围的再分割，也是学生易忽视的地方，如不加分割，函数单调性表述将不严密，还是容易丢分.