解析构造法在高中数学解题中的运用

夏碧芳

(福建省福州第十一中学 350001)

构造法包括构造方程、构造方程、构造数列等诸多内容，难度较大，要想灵活运用并非易事.教学中，为学生讲解构造法相关知识，使学生深入理解构造法，掌握构造法运用的注意事项.同时，精讲、优选典型例题以及训练题，使学生在听课、训练中，切实掌握构造法运用技巧，做到灵活运用.

一、构造方程的运用

解答部分高中数学试题时，经常需要构造一元二次方程，利用方程根与系数的关系以及Δ求解.为使学生能够熟练地构造方程，教学中，一方面，为学生讲解构造方程注意事项，即，要认真读题，结合题干构建已知条件与方程的桥梁，而非盲目地构造.另一方面，优选例题，板书通过构造方程解题的步骤，使学生认真体会，加以充分地理解与吸收.

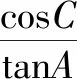
分析题干仅仅给出两个等式，直接求解的难度较大，很多学生不知道如何下手.教学中可引导学生认真观察两个等式，找到两个等式间的关系，通过构造方程解题.

解由16cosC+4sinB+tanA=0，可设4=t，则不难构造一元二次方程：(cosC)t2+(sinB)t+tanA=0.

Δ=sin2B-4cosCtanA,

又∵sin2B=4cosCtanA,∴Δ=0.

则关于t的一元二次方程有两个相等实根，即，t1=t2=4.由根与系数的关系得：

二、构造函数的运用

构造函数在高考中较为常见，常用于解答大题中某一问，难度较大.教学中，一方面，为学生讲解构造函数的技巧，如为两个函数，常通过作差构造新的函数，而后利用导数知识进行讨论.另一方面，优选有代表性的试题，对学生进行训练，使学生在训练中掌握构造函数解题的方法与步骤.

例2已知函数f(x)=x2+4x+2，g(x)=ex(2x+2)，若x≥-2时，f(x)≤kg(x)，求k的取值范围.

分析题干涉及两个函数，且给出“f(x)≤kg(x)”，可考虑运用构造函数法解题.

解由已知条件，构造函数F(x)=kg(x)-f(x)=2kex(x+1)-x2-4x-2.

则F′(x)=2kex(x+2)-2x-4=2(x+2)(kex-1).

由题设可知F(0)≥0且F(-2)≥0，

可得1≤k≤e2.

令F′(x)=0，解得x1=-lnk，x2=-2.

(1)当1≤k0.

可知在(-2，x1)上F(x)单调递减，在(x1，+∞)上,F(x)单调递增.因此在[-2，+∞)上最小值为F(x1)=-x1(x1+2)≥0.所以当x≥-2时，F(x)≥0，即f(x)≤kg(x)恒成立.

(2)当k=e2时，则F′(x)=2e2(x+2)(ex-e-2)，当x>-2时，F′(x)>0，即F(x)在(-2，+∞)上单调递增.而F(-2)=0，因此，当x≥-2时，F(x)≥0，即f(x)≤kg(x)恒成立.

综上可知k的取值范围为[1，e2].

三、构造数列的运用

构造数列解答数学试题，对学生的要求进一步提高，教学中，为帮助学生树立解题的自信，一方面，为学生讲解等差、等比数列基础知识，包括性质、通项公式、前n项和求解方法等，使学生打牢基础.另一方面，构造数列难度较大，教学中应结合具体题目，对学生进行解题上的引导，使学生尝到学习的成就感，自觉、认真掌握构造数列知识.

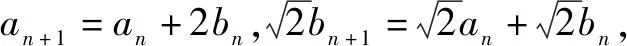
两式相减得：

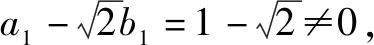
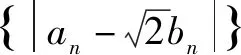
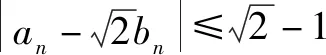
构造法虽是解答高中数学试题的有效方法，但其难度较大，教学中应注重教学研究，运用一定策略，使学生更好地掌握.一方面，教学中仍应将数学基础知识传授作为教学重点，而后再进行构造法知识的渗透.另一方面，为学生讲解各构造法的具体应用，鼓励学生认真反思，把握应用构造法的关键点，遇到类似数学试题能够迅速找到突破口.