简解函数由值域反求定义域问题

梁宗明

(甘肃省兰州市兰化一中 730060)

在高中数学中，在函数解析式已知的前提下，依据定义域求其值域的题型，非常常见，研究较多，但是，在函数解析式已知的前提下，依据给定值域反求其定义域的题型，并不多见，前者是顺向思维问题，结果唯一.后者是逆向思维问题，由函数的“映射定义”得出结论，一个y值可由多个x值与之对应，一般情况下，由函数的值域不能唯一确定其定义域，定义域结果无穷尽，难以掌握.除非函数是单调的.但数形结合思想可以轻松解决此类问题.

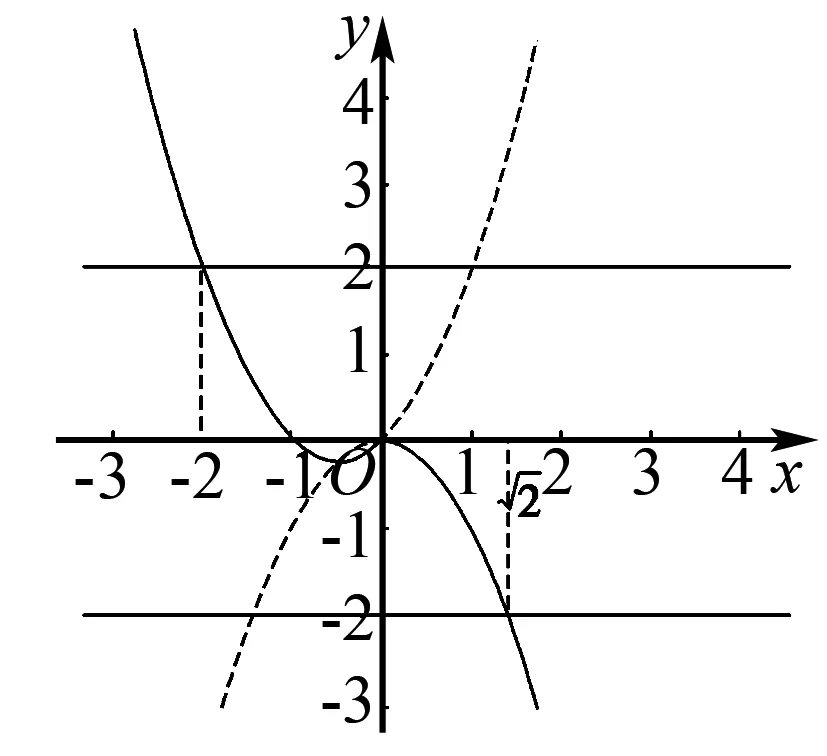
例2(2016·无锡模拟)已知函数y=x2-2x+3，在闭区间[0,m]上，y∈[2,3]，则m的取值范围为____．

解析作出函数f(x)的图象如图所示.当x=1时，y有最小值为2，当x=2时，y=3,当x=0时，y=3.满足y∈[2,3]的最小区间x∈[0,1]，满足y∈[2,3]的最大区间x∈[0,2].数形结合易得m∈[1,2]．

例3若函数y=4x-3·2x+3的定义域集合是A,值域y∈[1,7]，若集合B=(-,0]∪[1,2]，则集合A与B的关系____.

解析设2x=t,(t>0)，f(t)=t2-3t+3，当t=1或t=2时，y有最小值为1，当t=4时，y=7,当t=0或t=3时，y=3，当t∈(0,1]∪[2,4]时，y∈[1,7].如果规定t取其他范围的值，同样可以满足y∈[1,7].结合图象具体说明如下：作函数f(t)=t2-3t+3的图象，在(0,1]内任取a，在[2,4]内任取b，使得f(a)=f(b).

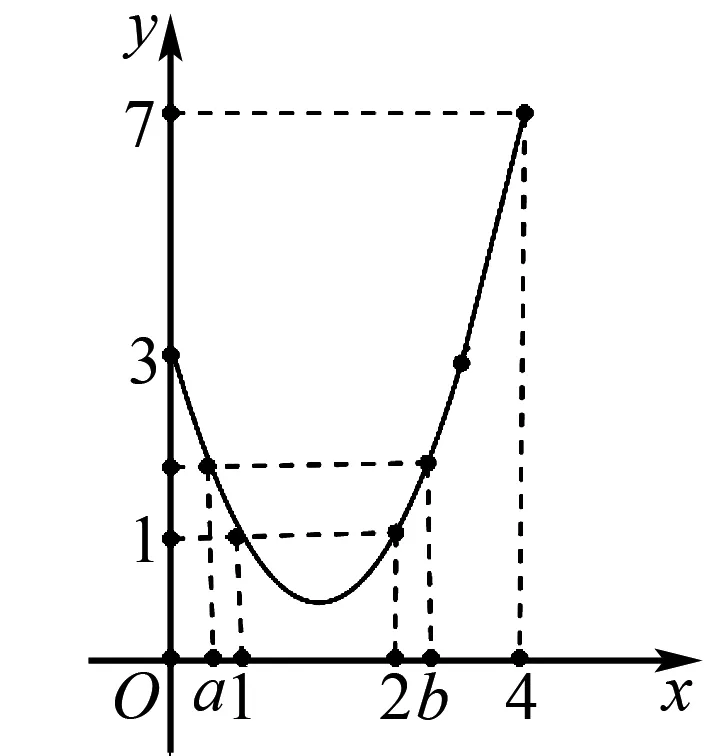
则t∈(0,1]∪[2,4]或者t∈(0,1]∪[b,4](b∈[2,3])或者t∈(0,a]∪[2,4](a∈(0,1]).依据a,b的不同值，满足题意的集合有无穷多个.但所有集合都是它的(0,1]∪[2,4]子集，显然(0,1]∪[2,4]是B=(-,0]∪[1,2]的子集.所以A⊆B.

点评根据函数的值域反求其定义域问题，属于不确定性的逆向问题，题目中一定有确定性条件支撑，以确定性条件为突破口，利用数形结合思想，研究满足值域的定义域的最小范围和最大范围是关键.