基于数学核心素养下的一节探究课
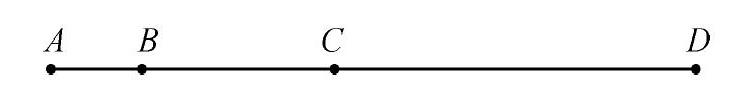

摘 要:随着我国教育工作的不断进步与发展,对于学生核心素养的培养已经成为教学工作的重要目标与任务之一,而在数学教学中,对于学生数学核心素养的培养主要是通过对学生关键核心解题能力与思维品质进行针对性的培养,进而实现学生的自主学习的目的。基于数学核心素养的理念下,开展教学的主要角度与方向是从自主学习能力、提出问题能力、创新思维能力三个方面入手,针对性的进行对学生数学核心素养的培养。
关键词:数学核心素养;探究课;逻辑推理;数学建模;直观想象
在教七年级数学几何内容时,经常会出现数线段、数角的个数,数三角形的个数等问题,七年级学生对这些问题困惑较大。因此,针对三角形的问题,我结合数学核心素养培养的理念开展了一趟探究课,开展探究课的主要目的就是对学生逻辑思维能力、数学建模思想、直观想象力等数学核心素养进行培养。经过探究课之后也收获了成果,并基本完成了目标,现整理成研究论文分享出来,旨在起到抛砖引玉的效果,希望各位同仁多多指正批评并提供更多教学思路,进一步推动对学生数学核心素养的培养效果。
一、 逻辑推理的素養
(一)题目与解法探究
在教学的第一步,为了实现逻辑推理能力的培养,我首先给学生出了一道题目:如下图,请学生观察并数出图中一共有多少条线段?按照分好的小组合作完成。
在题目布置之后,学生立刻开始了激烈的讨论,我在班里巡视了一周之后,听到有的小组答案不同,有的小组计算方式不同。
学生甲:共有6条线段,分别是线段AB、BC、CD、AC、BD、AD。
学生乙:我们也是认为6条,但是我们的计算方式是按照端点数量进行数线段,也就是通过A为左端点的线段先数,一共有3条:AB、AC、AD,再对以B为左端点的线段进行计算,一共有2条:BC、BD,最后再以C为左端点的线段进行计算,只有CD一条线段,把这些线段数量相加,所以共有3+2+1=6(条)线段。
此时全班一片赞扬声,可见乙同学的方法大家都认同。我抛出疑问:“甲同学的方法怎么理解?”第四组有同学发表看法说:“我认为甲同学的方法也可以写成算式3+2+1=6(条)。因为AB、BC、CD都只含有一条线段共3条,AC、BD是含有两段的线段,有两条,AD则是含有三段的线段,只有一条,所以共有3+2+1=6(条)。”
接着还是让学生通过小组合作的形式进行自主探究和交流研讨,学生在这个过程中可以真正感受自己发现问题、提出问题和分析解决问题的全过程,实现自主学习的目标与效果。
同学们各抒己见,一共归纳出了两种基本方法:按顺序数和分类数。
学生通过自己的思考与理解找到了结果,我看到了学生高兴的表情,同时我心里也非常的高兴。紧接着,为了进一步深化学生的逻辑思维推理能力,我又将问题深入:那么如下图,直线上如果一共有100个端点,那么一共有多少条线段呢?怎么计算?
我看到有的学生动手接着画了起来,也有的在掰手指头数,也有的小组讨论,气氛非常热烈,大家都在思考:这么多点怎么数呢?
面对学生的期待眼神,我故意不讲授方法,再次让学生经历主动探索,合作交流。过了几分钟,有同学举手了。
A小组代表:我们小组是按顺序数的,以第一点A1为左端点的线段有99条,以第二个点A2为左端点的线段有98条,依次下去,总共有99+98+97+…+2+1。
B小组代表:我发现第一个加数99刚好比点数100少1,然后每个加数依次少1,一直加下去,直到1为止。
C小组代表:我们组发现第一个加数就是间隔数99,因此线段总条数是1到间隔数99的所有自然数的和。
D小组代表:我们组是这样计算的,点数乘间隔数再除以2。
我先表扬了学生出色的表现和敏捷的思维,再对上述各种方法作了例证,在问题解决的全过程中培养学生的思维能力和创新能力,使学生积累数学思想和数学活动经验。最后,我把问题拓展:如图所示的图形中有多少个小于平角的角?有多少个三角形?我发现,在引导之下,学生基本上都可以将线段的计算思想迁移到三角形与角的思想中,这也令我非常的欣慰,这就说明学生的脑中已经建立起了基本的数学建模思想,并且已经会灵活运用数学思想去想问题、解决问题。
(二)教师追问
那么,数线段与数三角形、数角等问题之间有什么联系吗,可以共通吗?
学生都会感悟出方法相同,规律相同,这样数学模型水到渠成。
二、 数学建模——模型的应用
数学模型使得数学的应用具有广泛性。
拓展延伸1:我校七年级共有6个班,进行篮球赛,规定每两个班赛一场,那么我校7年级的篮球赛共要进行多少场?
学生面露自信之色,纷纷上台板演。学生代表甲说:7年级一共有六个班,类似于一条线段上六个不同的点,每两个班赛一场,类似于两点之间有一条线段,那么七年级篮球赛共有6×(6-1)÷2=15(场)。
拓展延伸2:乘火车从A站出发(铁路可抽象为一条直线)沿途经过7个车站(包括A站和B站)方可到达B站,那么在A、B两站之间有多少种票价?共需要安排多少种不同的车票?
这两题设计意图是借助孩子身边的事物(学校篮球赛,买车票等)引出数学知识,通过这些生活中常见的内容与数学知识、数学问题相结合,很好地让学生感受到了知识与生活的关联性,既能增强学生对于数学学习的积极性,同时也能培养学生的数学感觉与数学思维,发展学生的数学意识,而这个过程,就是培养学生数学核心素养的重要过程。
学生跃跃欲试,兴奋异常。学生乙说:第一问可转化为一条直线上有7个点时,共有线段7×(7-1)÷2=21(条)。即A、B两点之间共有21条不同的线段,因此有21种票价。因为来往两站的车票起点与终点不同,所以A、B两点之间需要安排21×2=42(种)不同的车票。
数学探究能力是学生数学素养的核心,也是数学核心素养的主要内容与本质,所以教师在引导学生数学核心素养养成的过程中要注意从简到难,不断地深化问题,深化思想,这样才能引导学生感受规律,进而有效地解决问题。
三、 直观想象,举一反三
数学教学工作中,直观想象能力也是一个重要的能力,教师应当注重学生对于问题理解的直观性,然后基于直观理解充分发挥学生的想象,锻炼学生养成举一反三的能力,这样才能使学生在解题思考的过程中逻辑正确,思维流畅。长此以往,学生会形成较好的思维逻辑能力与交流能力,通过对事物的本源的探究,增强学生对于数学的理解,深化核心素养,养成良好的数学学习习惯。
拓展延伸3:如果平面內n条直线相交,那么这些相交的直线最多会产生多少个交点?
拓展延伸4:如果小明组织了一次多人的聚会,聚会人数有n个,那么每两个人见面时会进行一次握手,在本次聚会中一共会有多少次握手?
拓展延伸5:现在有n支球队参加篮球比赛,赛制为单次循环的赛制,那么比赛结束之后,一共需要比赛多少场?
评析:上述第3~5问题万变不离其宗,学生仔细读题,若把n支球队看作一直线上有n个点,两支球队比赛看作过直线上两点连一条线段,则问题变为:一直线上有n个点,这n个点共能连成多少条线段?符合模型规律,问题迎刃而解。
四、 教学后反思
在开展完本次探究课之后,我发现大部分学生都具备基本的数学逻辑思维能力,而在引导下,学生也基本都进行了数学建模思想与直观想象的尝试,相较于传统的数学课堂教学来说,我认为主要的教学突破点在两个方面。
一个方面,学生的思维得到了很好的训练和发展,数学探究能力的提高是通过数学思维方法的训练来完成的。以往解决这类问题,传统的教学模式是老师讲解例题,讲完例题,学生模仿练习,靠大量习题的训练来完成,教师是课堂的主导者,学生则被动的按部就班,直接套用结论,知其然不知其所以然。这节课中,我把常态教学与数学核心素养的培养结合在一起,从学生能做的简单问题入手,逐步深入,通过观察,讨论和交流,归纳出数线段的两种基本方法(按顺序数和分类数),计算线段总条数的四种方法,并归纳出模型公式,将它拓展延伸到数角、数三角形、数车票、数比赛场数、数聚会握手次数等,学生的知识得到了升华,学生的思维也在独立思考和小组合作学习中得到了提升。特别是学生发现了
n(n-1)2(点数×间隔数÷2)的绝妙方法,创新思维能力得到提高,模型的得出水到渠成。
另一个方面,学生自主学习得到了很好的落实,发挥了学生的主体作用。本节课让学生采取小组合作的方式,探索求解数学问题,在教学设计上,把教学的重点设置成一个个有序的、层层递进的教学问题,并将数学的逻辑思维运用到生活中,在解决问题中寻找乐趣,以乐趣为驱动促进学习,调动学生学习的积极性。教师只是在关键性和概括性的语言表达上给予点拨和帮助,把“知识为导向的教学”转变为“以核心素养为导向的教学”,即从“以知识为本”转变为“以学生发展为本”或者说以“知识核心的时代”转变为“素养核心的时代”,小组合作学习真正落到实处,发挥了很好的作用。
参考文献:
[1]金烨.基于培养学生数学核心素养的课例研究[J].数学之友,2016(3):38-39.
[2]佚名.对基于数学核心素养的一节优质课的再思考[J].初中数学教与学,2018,394(22):16-18.
[3]佚名.基于数学核心素养目标下的课堂教学研究[C]∥教师教学能力发展研究科研成果集(第十七卷),2018.
作者简介:吴慧珍,福建省福州市,福建省福州市闽清县城关中学。

