基于边聚类系数的谱聚类社区划分方法研究

赵 菲， 余本国， 冀庆斌

(中北大学理学院， 太原 030051)

复杂网络的研究和理论建模是近年来物理和应用数学领域被大量研究的课题[1].关于复杂网络，钱学森给出了一个定义：具有自组织、自相似、吸引子、小世界、无标度中部分或全部性质的网络称为复杂网络.例如互联网、万维网、神经网络、代谢网络、社交网络等.近年来，随着对网络性质的不断探索，人们发现在实际网络中除了小世界特性和无标度等特性外，还存在着社区结构[2].社区即网络中节点的集合，属于同一社区内的节点之间的连接紧密，属于不同社区的节点之间的连接相对稀疏[3].对社区结构的研究有助于进一步发现网络中各个元素之间的关系.

学者们不仅关注到了网络中的社区结构，同时也提出了很多关于社区检测的算法，主要有：Kernighan-Lin提出试探优化算法[4]、基于Laplace矩阵的谱平均算法[5-6]、基于Normal矩阵的谱平分算法[7]、GN算法[8]，为了进一步降低算法的复杂度，Radicchi等人2004年在GN算法的基础上提出了边聚类系数法[9]等.2006年，Newman提出了基于模块度矩阵[10]的谱划分方法，将最大化模块度[2]函数的过程转化为线性代数中矩阵的谱问题，降低了算法的复杂度，并且得到了较好的划分结果.

边聚类系数也能很好的反映社区内节点的聚集程度，即社区内边构成的三角形的实际数目与所有可能包括该边的三角形的数目之比.社团内部的边被较多的三角形包含，相应的该边的聚类系数较大；社团之间的边被较少的三角形包含，甚至不被三角形包含，相应的边聚类系数较小.鉴于此，本文在边聚类系数的基础上，定义了聚类系数矩阵和增益函数，将最大化增益函数的过程转化为了矩阵的特征值和特征向量的求解问题.最后将该方法应用于Zachary空手道俱乐部网络、dolphins海豚网络，Blogs网络的真实网络中，将实验结果与真实网络的分组结果相比较，结果表明该算法可行.

1 相关工作

1.1 基于拉普拉斯矩阵的图分割

在计算机上进行图划分已经被人们大量的研究，把网络中的图划分就是把网络的节点划分成组，使组之间的边数最小化.各种方法中使用最广泛的就是由Fiedler提出且由Pothen等人推广的谱分割[5，11]，通过拉普拉斯矩阵的特征值和特征向量实现图分割.

在无向网络中，首先定义邻接矩阵wij：

(1)

图划分把相似度高的节点归为一组，使组之间的连接边数达到最小.定义两组之间连边数目为H，其中节点i，j分别属于不同的组，如下式：

(2)

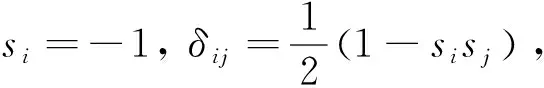
(3)

连接节点i的边的总和即节点的度[12]，记为di，则H可以写为

(4)

用矩阵形式表达H，可写为

(5)

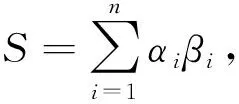
(6)

式中，μi是L的特征值，βi是对应于特征值的特征向量，把特征值以从小到大的顺序排列为μ1≤μ2≤μ3≤…≤μn，选择第二小特征值对应的特征向量，即Fiedler向量.当Fiedler向量中的元素大于或等于0时，该元素对应于索引向量中的+1；当Fiedler向量中的元素小于0时，对应于索引向量中的-1，从而将网络中的节点划分为两组.

1.2 边聚类系数

朋友关系网中，你的两个朋友之间也可能是朋友，这种属性在复杂网络里称为网络的聚类特性[13].Radicchi等人2004年提出了计算边〈i，j〉的边聚类系数(edge clustering coefficient)[9，14]，如下式：

(7)

2 聚类系数矩阵与社区划分

2.1 聚类系数矩阵与增益函数

本文定义聚类系数矩阵的思想是，连接不同社区的边〈i，j〉包含在少数三角形中或者不被三角形包含；处于同一社区内的边〈i，j〉包含在较多的三角形中，可见以边〈i，j〉构成的三角形大多存在于社区中.在无向网络中，已知式(1)邻接矩阵wij，定义Cij为聚类系数矩阵，当网络中的节点i和j之间有边连接，且节点i和节点j都与节点u相连时，Cij=1.如下式：

(8)

复杂网络的一个明显特征是社区结构，即整个网络是由许多社区构成，社区则是指网络中的一些聚集程度较高的群体.通过边聚类系数的定义可知，在复杂网络中一个节点聚集程度高的社区内，含边〈i，j〉的三角形的数量相对较多.为了使社区内的含边〈i，j〉的三角形的数量较多，使社区内节点的聚集程度更高，提出一种新的划分社区的指标，即把社区内部的含边〈i，j〉的三角形的数量与可能的含边〈i，j〉的三角形的数量相比较.通常情况下，在具有社区结构的网络中，两者的的差值大于0，反之，当差值小于0时，网络中则不存在社区结构.

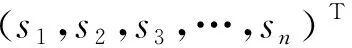
(9)

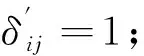
定义增益函数Z如下：

(10)

2.2 网络的社区划分

在网络的划分中，要使社区结构划分越明显，需要最大化增益函数.现在考虑将网络划分为两个社区.

将式(10)写为：

(11)

类比于式(5)，得到

(12)

其中E是实对称矩阵，定义为聚集矩阵

E=Cij-Mij.

(13)

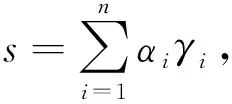
(14)

式中，φi是矩阵E的对应于特征向量γi的特征值，不同于拉普拉斯矩阵图划分中的使H达到最小，这里使增益函数达到最大值.令特征值由大到小排序为φ1≥φ2≥φ3≥…≥φn，最大化E的值即选择合适的αi的值，把最大化的任务赋予最大的φi所对应的量.由于si=±1，意味着si通常不能与γi平行选择.与上述一样，通过选择si尽可能与γi平行，可以获得良好的近似解.如下式：

(15)

2.3 算法流程

输入：网络G(V，E).

输出：社区划分结果.

(a)m=V，将G(V，E)表示为邻接矩阵，利用公式(8)得到Cij；

(b) 计算3个节点i，j，u同时连接的数量Mij；

(c) 计算聚集矩阵E=Cij-Mij；

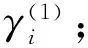
从表4和图8～图9中可以看出，基于WV-CNN的语义相似度计算模型明显优于基于字面匹配的语义相似度计算模型LCS和TF-IDF，在Accuracy、F1、AUC、KS值的评价指标上均有较大幅度的提高。LCS与TF-IDF在Accuracy、F1两个指标上相同，而TF-IDF的AUC值低于LCS的AUC值并且差距较大；在WV-CNN模型中，SGD优化器的效果优于RMSProp优化器，准确率随着训练集数据量的增加而增加。

(f) 标记已知分组情况的社区1与社区2，以不同形状标记；

(g) 出图；

(h) 算法结束.

3 实验结果与分析

本节在3个真实的网络中进行实验，对于社区结构明显的网络，通过与网络的实际划分情况对比得出结论；对于社区结构不明显的网络，通过与拉普拉斯矩阵的谱方法进行对比，以验证本文提出的基于聚类系数的谱方法划分社区的有效性.网络的基本信息如表1．

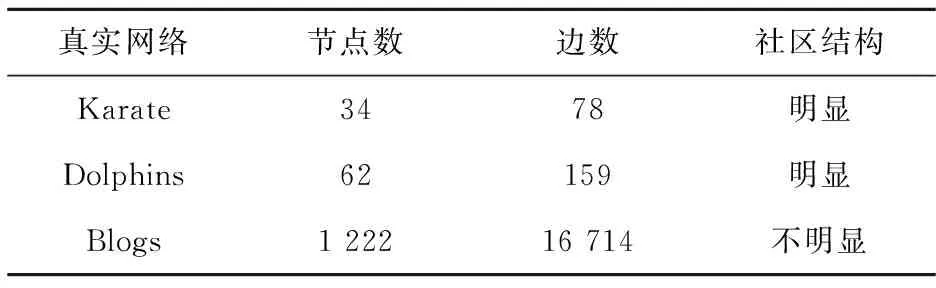
表1 真实网络的基本数据信息

3.1 实验1

Zachary在20世纪70年代用了两年的时间观察美国一所大学中的空手道俱乐部34个成员间的相互社会关系[15]，由于该俱乐部主管与校长之间产生争执，俱乐部分裂成了两个分别以主管和校长为核心的小俱乐部.在该网络数据上进行实验，如图1所示，网络由34个节点和72条边组成，菱形和长方形分别代表俱乐部成员的真实分组情况，颜色的区分代表了用本文的方法划分的结果.图2中，横坐标表示节点的标号，纵坐标表示当特征值φ1=1.7877时，所对应的特征向量中元素的取值，以0值为分界线表明了分组情况.由实验结果可知，使用基于聚类系数矩阵的社区划分结果与实际的划分结果一致.

3.2 实验2

关于社团划分，还有一个经典的例子是海豚网络，生活在新西兰神奇峡湾的62只海豚，在一个关键成员离开后分成了两个较小的子群.如图3所示，网络由62个节点和159条边构成，圆形和方形分别代表网络的真实划分情况，颜色的区分代表了用文中所述的方法划分的结果.从图上看，只有标号为29，31，40的三个节点没有划分到正确的社区中，非常接近于实际的划分.图4纵坐标表示为，当特征值φ1=3.5177时，所对应的特征向量中元素的取值，并以0值为分界线，展示了节点的分组情况.

图1 空手道网络社团划分Fig.1 Community division of the karate network

图2 特征向量中元素的取值分布Fig.2 Distribution of elements in eigenvectors

图3 海豚网络社区划分Fig.3 Community division of the Dolphin network

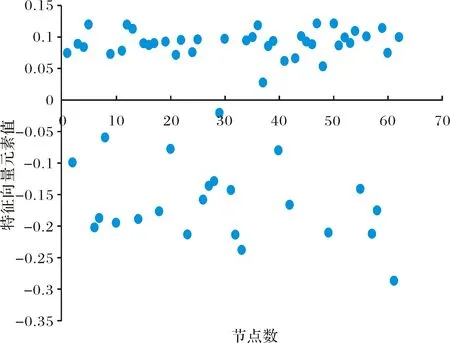
图4 特征向量中元素的取值分布Fig.4 Distribution of elements in the feature vector

从划分结果来看，使用聚类系数矩阵划分社区与使用模块度矩阵的谱算法得到了一样较为准确的划分结果，说明本文提出的方法具有一定的可靠性.

3.3 实验3

本文的方法在具有明显社区结构的网络中都有较好的体现，现将方法运用于社区结构不很明显的Blogs网络，该网络由1 222个节点构成.图5为基于拉普拉斯矩阵的谱方法划分网络的节点分布图，其中横坐标代表节点数，纵坐标表示拉普拉斯矩阵的第二小特征值对应的特征向量中元素的取值，以纵坐标0值为两组的分界线，可见，该网络的社区划分效果并不理想.

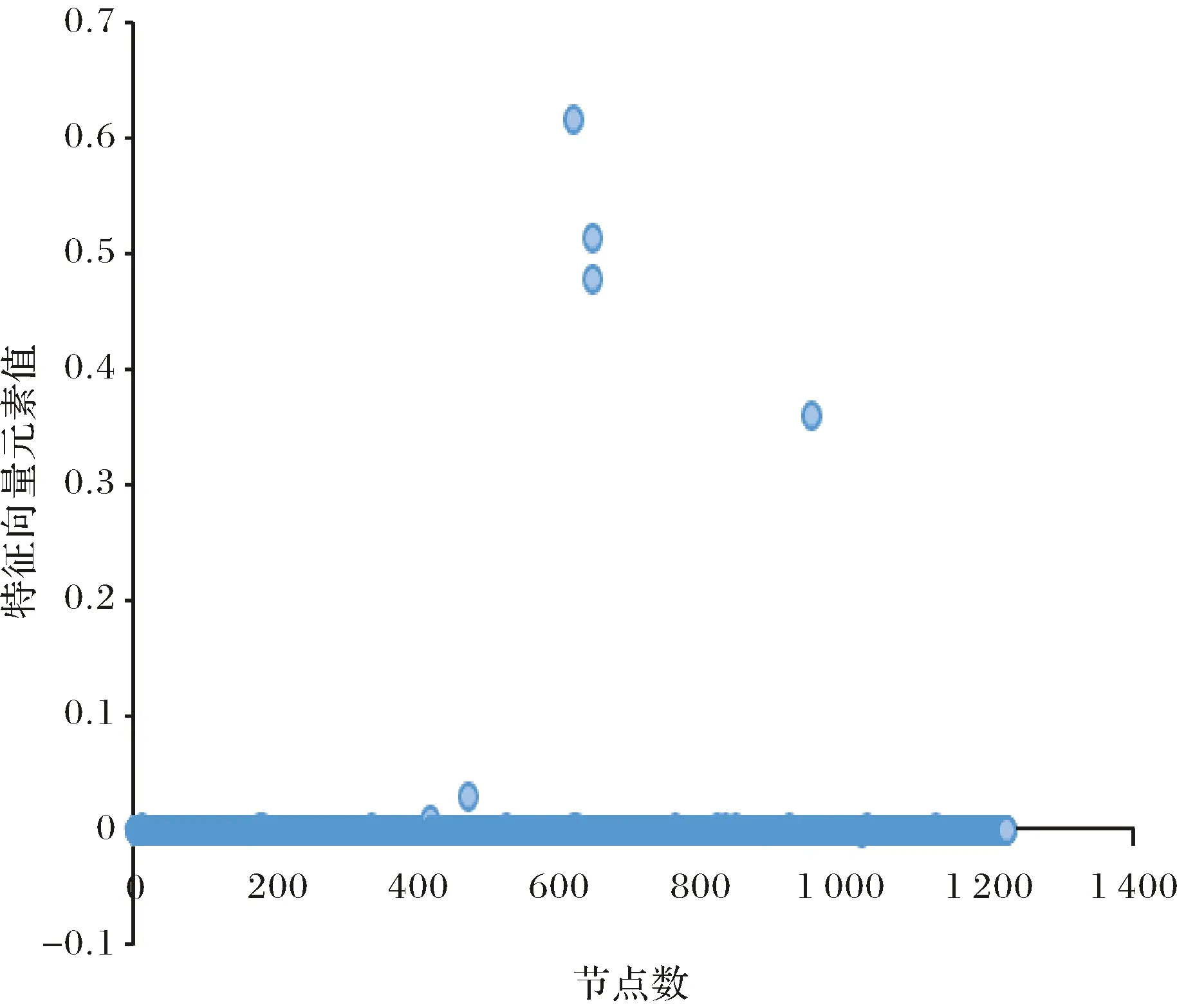
图5 拉普拉斯矩阵节点分布图Fig.5 Node distribution diagram of Laplacian matrix

图6为用本文所述的基于聚类系数矩阵的谱方法划分网络的节点分布图，其中横坐标表示节点数，纵坐标表示对应于最大特征值的特征向量中元素的取值，以纵坐标0为两组的分界线，较图5的方法，blogs网络被划分成为相对明显的两个社区.

从划分结果来看，对于社区结构不是很明显的网络，本文提出的方法也能较好的划分社区.

图6 聚类系数矩阵节点分布图Fig.6 Node distribution map of clustering coefficient matrix

4 结束语

由于社区内部节点之间的连接较稠密，社区之间节点的连接较稀疏，边聚类系数很好地表示了图中节点的聚集程度，即社区内部的连接边被较多的三角形所包含，社区间的连接边被较少的实际三角形包含，因此网络的社区划分也可以从社区内部与社区之间包含的三角形数量来考虑.从这个角度出发，本文提出了基于聚类系数矩阵的谱方法来对社区进行二分，首先构造了聚类系数矩阵，定义了增益函数，将最大化增益函数的过程转化为线性代数中矩阵的谱问题，通过求聚集矩阵最大特征值对应的特征向量，判断特征向量中元素的符号，把网络划分为两个社区.通过实验，将该算法应用到3个实际的网络中，不仅在Zachary空手道俱乐部和海豚这两个社区结构较明显的网络中得到了很好的划分结果，在社区结构不是很明显的blogs网络，相比传统的谱方法，也有了一定的提高.文中所述的方法在二分网络中都具有良好的表现.在现实网络中往往不只有两个社区，如何将该方法应用于网络的多社区划分，将是今后研究的重点.