分数阶Birkhoff系统的积分因子与守恒量
杨丽霞, 张 毅
(1.苏州科技大学数理学院, 江苏 苏州 215009; 2.苏州科技大学土木工程学院, 江苏 苏州 215011)
在研究相关的动力学问题时,分数阶微积分产生了重要作用.在实际应用中,分数模型较整数阶模型而言,更加符合实际意义,结论更加精确.1996年,Riewe首次建立了非保守力学系统的分数阶模型[16-17].随后,Frederico和Torres建立了分数阶Lagrange系统和分数阶Hamilton系统的Noether定理[18-19].近年来,分数阶模型下约束力学系统的守恒量研究已经取得重要进展[20-25].张毅等[26]提出并证明了Riemann-Liouville导数下分数阶Birkhoff系统的Noether定理,束方平等[27]将积分因子法应用于分数阶Lagrange系统.本文将用积分因子法研究基于Riemann-Liouville导数的分数阶Birkhoff系统的守恒量,从而建立该系统的积分因子定义与守恒定理.
1 Riemann-Liouville分数阶导数及其基本性质
假设在区间[a,b]上,函数f(t)连续且可积,则Riemann-Liouville分数阶左导数定义为
(1)
右导数定义为
(2)
其中,Γ(*)是Gamma函数,α是导数的阶,且0≤α<1.
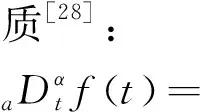
(3)
(4)
(5)
(6)
(7)
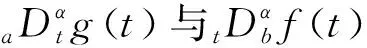
2 分数阶Birkhoff系统及其积分因子
由2n个Birkhoff变量aμ=aμ(t)来描述的分数阶Birkhoff系统,该系统的Birkhoff函数为B=B(t,aν),Birkhoff函数组为Rμ=Rμ(t,aν),在Riemann-Liouville导数下分数阶Birkhoff方程可表示为[26]
(μ,ν=1,2…,2n).
(8)
如果α→1,则方程(8)成为
(μ=1,2,…,2n),
(9)
方程(9)是经典Birkhoff方程[2].
定义1如果存在函数集ξμ(t,aμ),使得不变式
恒等地化为
(10)
其中,函数G,ξ0和λμ与t,aμ相关,则称函数集ξμ(t,aμ)是分数阶Birkhoff方程(8)的积分因子.
3 分数阶Birkhoff系统的守恒定理
假设函数集ξμ(t,aμ)是方程(8)的积分因子,将式(8)代入式(10),得到
(11)
故有
命题1若函数集ξμ(t,aμ)是分数阶Birkhoff方程(8)的积分因子,那么沿着系统的运动微分方程,存在守恒量I(t,aμ),形如
(12)
如果分数阶Birkhoff系统(8)存在积分因子ξμ,则守恒量I中的函数集G,ξ0,ξk一定满足必要条件(10).由式(8),可将(10)化简成
(13)
展开上式,并将式(8)代入,得到
(14)
如果必要条件(14)的解G,ξ0和ξμ使得表达式(12)等号右边成为一个常数,即
若C0为定值常数,则可称此组解G,ξ0,ξμ为奇异函数组;反之,若C0为任意常数,则可称此组解为非奇异函数组.故有如下命题.
命题2对于分数阶Birkhoff系统(8),若有非奇异函数组G,ξ0,ξk和λμ为必要条件(14)的解,则该分数阶Birkhoff系统存在一个形如式(12)的守恒量.
命题1和命题2统称为积分因子理论.
4 广义Killing方程
用上述积分因子理论寻找该系统(8)的守恒定理的过程中,重点是需要找到非奇异函数组G,ξ0,ξk和λμ,满足其必要条件等式(14).
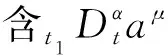
(15)
(μ=1,2,…,2n).
(16)
方程(15)和(16)是关于(4n+2)个未知函数G,ξ0,ξμ和λμ的(2n+1)个偏微分方程.因此,寻找必要条件(14)的非奇异函数组解便转化为寻找式(15)和(16)的非奇异函数组解.从式(15)和(16)的方程中可以看出,其未知函数的个数明显多于其广义Killing方程式的个数,因此该方程组的解不唯一.在寻找其广义Killing方程的解过程中,可先适当选取部分G,ξ0,ξμ,λμ的值,便可得到方程(15)和(16)的解,故可求得此系统的守恒量.
命题3对于所论分数阶Birkhoff系统(8),若广义Killing方程(15)和(16)存在非奇异函数组解G,ξ0,ξμ,λμ,则该系统(8)存在一个形如式(12)的守恒量.
此外,为了得到非奇异函数组解G,ξ0,ξμ和λμ,也可将该系统方程(8)直接代入必要条件(14),得到
(17)
可以通过直接解方程(17),得到非奇异函数组解G,ξ0和ξμ,从而得到此系统(8)的形如式(12)守恒量.
5 特例——分数阶Hamilton系统的积分因子
由Lagrange系统、Hamilton力学系统的从特殊到一般的发展,有了Birkhoff力学系统.
若取
B=H,
(18)
其中,qk和pk分别为广义坐标和广义动量,H=H(t,qk,pk)为Hamilton函数,则可将分数阶Birkhoff系统(8)退化为如下分数阶Hamilton方程
(19)
由定义1,得到下面定义2.
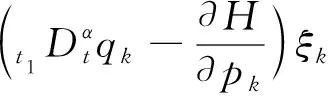
(20)
其中,函数G,ξ0,λk与t,qk,pk相关,则称函数集ξk=ξk(t,qk,pk)是该系统方程(19)的积分因子.
由命题1和命题2便可得下面命题4.
命题4若函数集ξk(t,qk,pk)是该系统方程(19)的积分因子,则由该分数阶Hamilton系统的运动微分方程存在守恒量I,形如
(21)
命题5对于分数阶Hamilton系统(19),若有非奇异函数组G,ξ0,ξk和λk为必要条件
(22)
的解,则此系统存在一个形如式(21)守恒量.
(23)
(24)
命题6对于分数阶Hamilton系统(19),若有非奇异函数组G,ξ0,ξk和λk为广义Killing方程(23)与(24)的解,则此系统存在一个形如式(21)守恒量.
6 算例
若分数阶Birkhoff系统的Birkhoff函数B和Birkhoff函数组Rμ分别为
(25)
R1=a2,R2=0,R3=a4,R4=0.
(26)
分数阶Birkhoff方程(8)给出
(27)
将式(27)代入广义Killing方程(15)和(16),得到
(28)
(29)
(30)
方程(28)~(30)有解:
(31)
(32)
(33)
(34)
由命题3可得
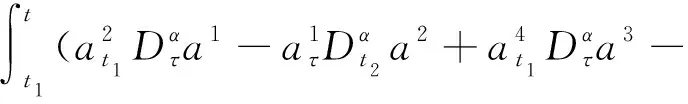
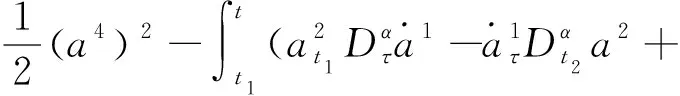
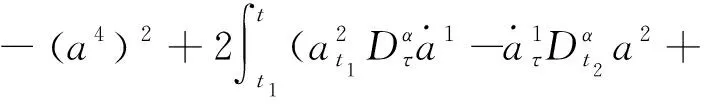
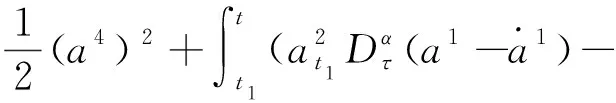
方程的解(31)~(34)是非奇异函数组解,故I1、I2、I3、I4是系统的守恒量.
7 结论
寻找约束力学系统的守恒量是分析力学研究的重要内容,积分因子法因其计算简单,适用范围广而得到广泛应用.文章的主要工作:一是定义了分数阶Birkhoff方程(8)的积分因子;二是建立了由积分因子理论得到的分数阶Birkhoff系统的守恒定理,由其积分因子理论得到了该系统的守恒量形式;三是建立了分数阶Birkhoff系统的广义Killing方程,给出了求解守恒量的具体方法;最后给出分数阶Hamilton系统的积分因子定义,并给出其守恒定理.文章的方法和结果可进一步推广及应用于基于不同分数阶导数的分数阶约束力学系统.

