液压驱动冗余并联加载机构耦合特性分析和控制

(航空工业庆安集团有限公司， 陕西西安 710077)

引言

铰点空间控制方法因结构简单、容易实现的优点，被广泛应用于并联机构的运动控制[1-4]。然而并联加载机构常因其自身结构布置和试件特性的影响，机构各支链通道和各自由度间存在强动力学耦合，这种耦合作用随着并联机构的位姿变化而发生变化，控制器增益的调节会严重受到系统低阶模态的限制[5-6]。为降低耦合特性对系统控制性能的影响，动力学前馈控制、计算力矩控制和模态空间控制等基于动力学的控制方法[7-10]被提出，但由于动力学模型往往存在高度非线性和时变性，实际控制效果受到较大影响。基于运动学的交叉耦合控制方法[11]需要使用运动学正解，实时性要求高，且控制结构复杂，需调整的控制增益较多，实际应用较为困难。

本研究以9条液压缸驱动的六自由度冗余并联加载机构为对象，通过对加载机构耦合特性进行分析，提出一种空间转换控制方法，并仿真对比分析与采用传统铰点空间控制下系统的控制性能。此外，当并联机构采用冗余驱动时，运动控制还应考虑内力耦合问题，内力抑制方法[10，12]不作为本研究的研究范围。

1 机构描述

如图1所示，加载机构的下平台通过9条对称液压缸与加载框架底部相连，连接铰均为虎克铰。将外侧布置的6条液压缸，定义编号为1～6，内侧布置3条液压缸，定义编号为7～9，每条液压缸配有内置式LVDT位移传感器，且在活塞杆轴向前端安装有力传感器。外侧6条液压缸的上、下铰点分别位于半径为ra和rb的圆周上。上铰点之间和下铰点之间的连线各构成一个标准的六边形结构。2个六边形的布置方向相差180°。内侧3条液压缸呈120°均布，处于以z轴为轴心的圆锥面上，上、下铰点各位于半径为ru和rl的圆周上。加载试件上、下端分别固定在加载框架和上平台上。

图1b为加载机构的俯视图，定义体坐标系Op-xpypzp固定在加载机构上平台上，惯性坐标系Ob-xbybzb固定在基础上。当机构位于初始中位时，两个坐标系重合在上平台表面中心处。

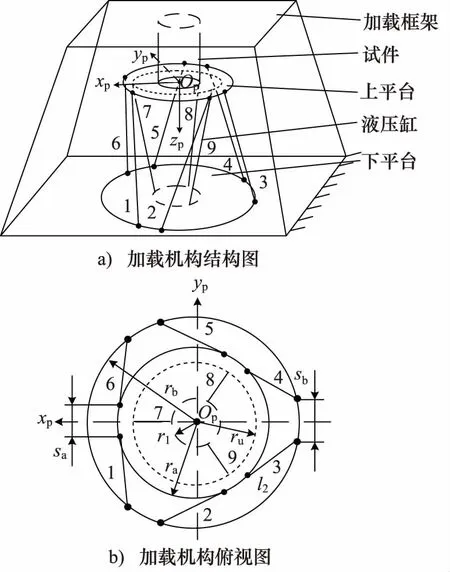
图1 六自由度液压驱动冗余并联加载机构结构图

2 耦合特性分析

将加载机构中的液压缸视为液压弹簧，与加载试件弹性环节并联，可得如图2所示的自由振动模型。通过研究加载机构的模态特性以观测加载机构自由度间耦合情况。

考虑液压缸缸筒、活塞杆等质量影响，建立系统完整的动力学模型，简化表示成下式：

式中，q为上平台位姿向量，q=[x,y,z,φ,θ,ψ]，其中x,y,z为3个平动自由度；φ,θ,ψ为绕x,y,z3个轴对应的转动自由度；M,C,Ks,G分别为惯性坐标系下质量矩阵、离心力及科氏力系数矩阵、加载试件刚度矩阵、重力项；f为9条液压缸出力组成的力向量；J为机构雅可比矩阵。

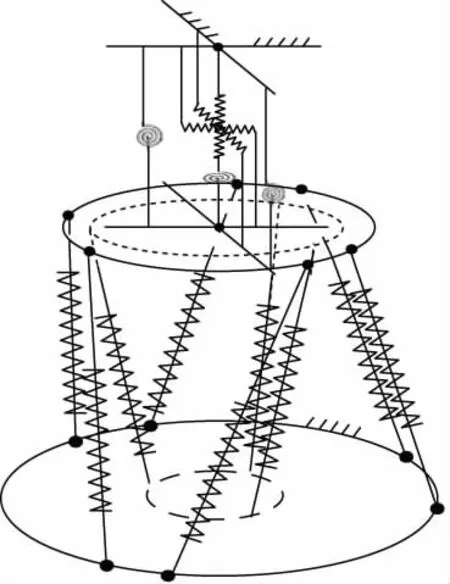
图2 加载机构自由振动模型

第i条液压缸等效液压弹簧刚度khi可写为：

(2)

式中，βe为有效体积弹性模量；Ai,Vti分别为第i条液压缸有效果面积和左右腔室的总体积。

则9条并联液压弹簧在广义坐标上等效刚度Kq可写为：

Kq=JTKhJ

(3)

式中，Kh为液压弹簧组成的对角矩阵，Kh=diag(k1,k2, …,k9)。

与试件刚度Ks并联后总的刚度矩阵K为：

K=Kq+Ks

(4)

则加载机构自由振动模型的振动微分方程可表示为：

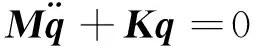
(5)

因为方程式(5)中的质量矩阵、刚度矩阵是关于平台位姿的函数，这里考虑平台处于中位时的模态特性。

计算中位时加载机构模态频率ωm=[17.2， 17.2,41.09,42.53,42.53,32.93] Hz，模态矩阵U为：

(6)

由此分析该加载机构在中位时第一、二阶模态频率相等，主要映射在x和y平动方向，对应系统的最低模态频率；第三阶模态映射在ψ方向；第四阶模态映射在z平动方向；第五、六阶模态频率相等，主要映射在φ和θ方向。从模态矩阵U中可以看出，z和ψ自由度在中位时和其它自由度无耦合；由于试件的刚度耦合特性和加载机构的非正交结构布置，x和y自由度分别受到θ和φ自由度强动力耦合影响；对应于φ,θ,z3个方向的模态频率较高。加载机构内侧布置的3个液压缸增加了垂直平面内3个自由度φ,θ,z的刚度，减小了其它自由度动力耦合干扰的影响。

3 控制方法

通过耦合特性分析，加载机构各自由度间存在强动力学耦合。采用传统的铰点空间控制方法时，由于各支链单通道间耦合更为严重，调节任意一个通道的控制器参数增益均会同时影响到6个自由度通道的动态性能，故控制器所有通道增益的调节会严重受到系统最低阶模态频率的限制，控制性能因此会大大降低。

为降低强耦合特性影响，当采用基于自由度的控制方法或基于运动学的交叉耦合控制方法时，为获得良好运动控制精度，需要使用运动学正解实时解算平台当前位置和雅可比矩阵，增加了实施难度，因此本研究提出一种空间转换的控制方法，如图3所示。图中的外部回路类似于铰点空间控制方法，根据给定位姿q反解出各液压缸所需的运动量l，再与各液压缸运动反馈量lm进行比较，形成各液压缸独立位移闭环控制。不同的是在内部回路通过雅可比矩阵伪逆J+将液压缸位移控制误差el转换成自由度控制误差eq，从而转换到自由度空间上进行控制器设计，直接根据各自由度通道的动态特性进行相应的控制器参数调整，降低强耦合特性的影响，控制器通道数量也由传统铰点空间控制的9个减少为6个。最后由雅可比矩阵J将自由度控制量uq分配给各伺服阀控制量u去驱动液压缸运动。虽然使用的雅克比矩阵J为给定位姿经运动学反解解算的近似值，但由于最终闭环控制的为各液压缸运动量，故对控制性能影响较小。

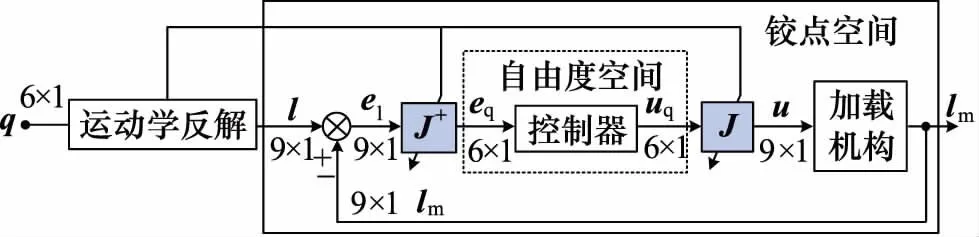
图3 空间转换控制方法

4 仿真分析

同时给定3个平动和3个转动自由度阶跃指令信号，幅值分别为2 mm和0.2°。为更加直观地对比采用传统的铰点空间控制方法和空间转换控制方法下位姿响应性能，控制器均使用简单的比例控制。铰点空间控制参数调整时，受最低阶模态性能的限制，在保证系统响应稳定情况下，最终调节铰点空间控制器增益矩阵Kpj=diag(3,3,3,3,3,3,3,3,3)。空间转换控制参数调整时，可将对应于最低阶模态且受到来自φ,θ自由度动力耦合的方向x,y对应的自由度控制器增益调至较小值，从而保证系统足够的稳定裕度，将对应于高阶模态的自由度方向φ,θ,z控制器增益调至较大值，以获得较高的位姿响应性能，最终调节空间转换控制器增益矩阵Kpd=diag(3,3,8,6,6,6)。

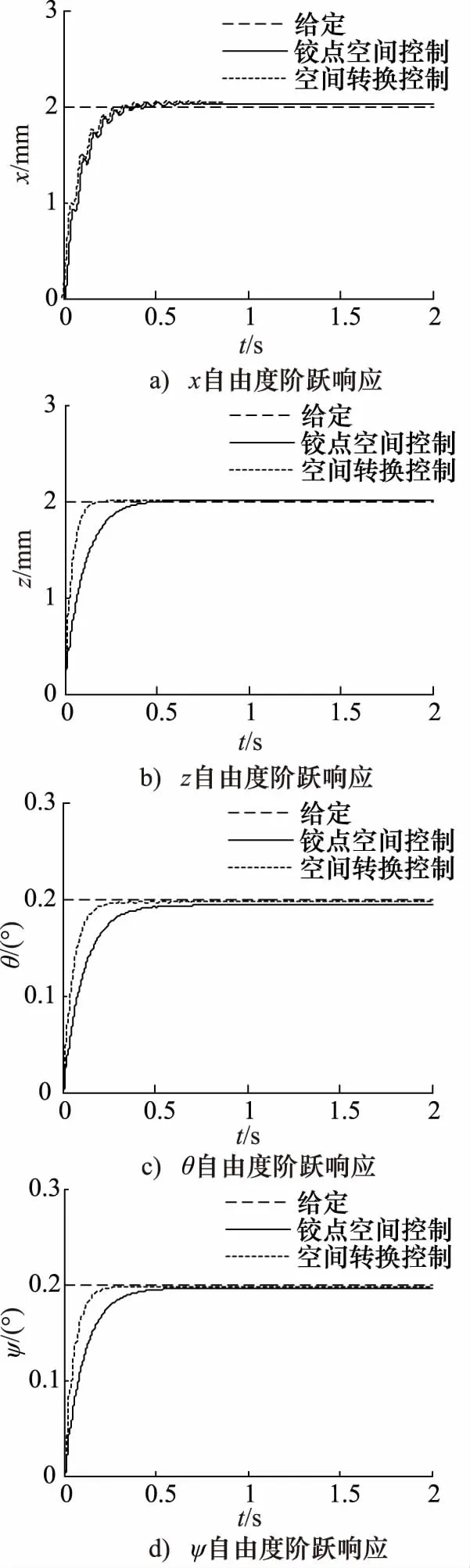
图4 两种控制方法下各自由度阶跃响应情况

x,z,θ,ψ4个自由度阶跃响应仿真结果如图4所示，可以看出受到最低阶模态频率的限制，两种控制方法下在x方向阶跃响应情况相似，其中x方向产生正的稳态误差主要是受到θ方向干扰力的影响，液压系统低阻尼特性造成上升过程中出现抖动现象。而空间转换方法在z,θ,ψ3个自由度的响应速度更快，稳态精度更高，这主要是由于空间转换控制方法可以根据各自由度通道的动态特性，在转换的自由度空间上对各自由度控制通道增益进行单独调节，有效降低耦合的影响，提高位姿响应性能。

5 结论

本研究分析了由9条液压缸驱动的六自由度冗余并联加载机构的耦合特性，并提出了一种空间转换空间控制方法，将铰点空间控制误差量转换到自由度空间后，直接根据各自由度通道的动态特性进行相应的控制器参数调整。

仿真结果显示，比起传统的铰点空间控制，提出的方法有效降低了机构强耦合特性对铰点空间下控制器增益参数整定的影响，提高了位姿响应性能。同时避免了使用运动学正解对系统高实时性要求，且减少了控制器需调整增益数目，具有较好的工程应用价值。