液压支架矿用液压缸动载过载特性的仿真及试验研究

唐小龙， 王晓东

(1.煤炭科学技术研究院有限公司， 北京 100013； 2.煤炭资源高效开采与洁净利用国家重点实验室， 北京 100013)

引言

随着我国煤矿深度和强度的增大，冲击地压灾害发生的频度和强度明显增强，冲击地压矿井数量呈上升趋势。液压支架立柱(一种液压支架矿用液压缸，以下简称液压缸)是液压支架主要承载部件，提高立柱的抗冲击能力是应对井下冲击地压，实现安全高效开采的有力技术手段。要提高液压缸的抗冲击能力，必须对液压缸的动载特性(动态载荷作用下的特性)进行深入分析。目前的研究成果大多集中在理论分析方面：基于有限元分析原理、光滑粒子流体动力学、流固耦合原理模拟液压缸在动载过载条件下动态响应，对液压缸在动载过载下缸体的应力、应变分布规律[1-3]。针对静载条件下液压缸结构件危险截面及最大应力进行仿真计算并分析其影响因素[4-5]； 基于 AMESim软件建立液压回路系统模型，模拟煤壁顶板振动作用下以及蓄能冲击作用下液压回路系统以及液压缸无杆腔压力、流量特性[6-10]；利用经典力学公式推导得出落锤冲击作用下的液压缸内腔压力波动方程、煤壁顶板作用下液压缸内液体压力的解析表达式，对液压缸压力特性进行数值计算，并通过建立挠度微分方程计算静载载荷条件下液压缸失稳的临界条件[2,7,11]。

目前由于缺少试验设备及技术条件，针对液压缸在动载过载条件(高于液压缸额定工作载荷的冲击载荷作用)下液压缸结构件的应力分布和压力特性的试验研究相关工作尚未开展。针对液压缸在不同额定压力倍率下的动载过载特性，结合AMESim和ANSYS workbench仿真软件对液压缸在动载过载条件下的结构件应力分布、液压缸内腔压力波动情况进行模拟计算。为了验证仿真模型搭建以及简化条件是否合理准确，在模拟计算的基础上设计试验测试方案，应用蓄能冲击原理对液压支架液压缸进行动载过载特性试验，并同步进行应力应变测试以及压力监测得到测试数据，综合分析仿真数据与试验测试，对液压缸动载过载特性进行分析研究。研究结果为液压缸在动载条件下的预期破坏位置及液压支架抗冲击液压缸优化设计提供理论指导和试验数据参考。

1 AMESim动载加载仿真分析

液压缸动载过载加载系统采用蓄能冲击原理，加载条件参考国家标准GB/T 25974.2-2010《煤矿用液压支架第2部分: 立柱和千斤顶技术条件》，单伸缩立柱(矿用液压缸)初撑充液后闭锁压力腔，蓄能器开启将高压油液瞬间注入柱塞冲击缸，柱塞缸柱塞动作轴向撞击液压缸，使液压缸下腔压力在30 ms内由0.6倍额定压力达到设定的不同倍率额定压力[12]。

1.1 蓄能器压力参数计算

共进行1.0, 1.1, 1.2, 1.3, 1.4, 1.5倍额定载荷动载过载仿真分析。为达到预期内腔压力，根据液压缸性能参数(如表1)对蓄能器设定参数计算[13-15]，计算结果如表2所示。

表1 被试件性能参数表

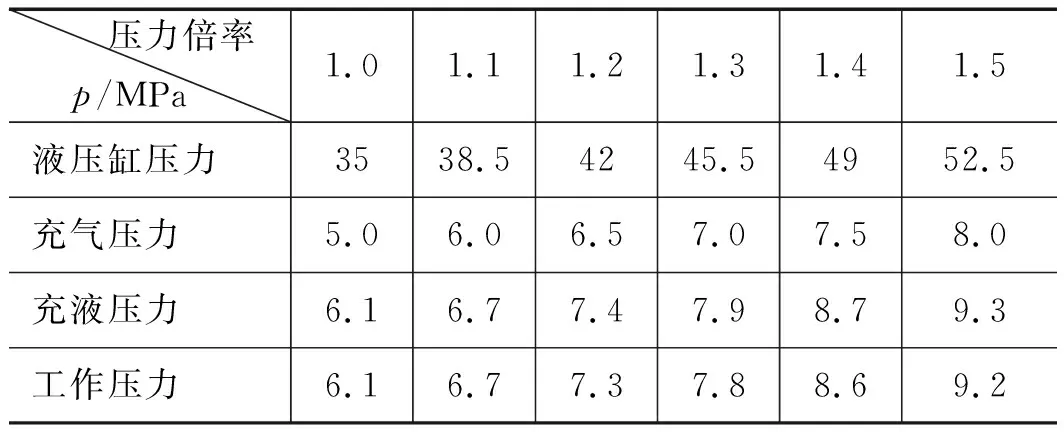
表2 蓄能器压力参数

1.2 模型设计

根据上述加载原理运用AMESim软件标准液压库和液压元件库、液阻库以及机械库，构造各个液压元件的仿真模型，并为各个元件选择合适的子模型，搭建的动载加载系统模型如图1所示。

1.3 子模型参数设置

以1.5倍动载过载仿真分析为例介绍AMESim仿真内容，表3为模拟元件子模型的具体参数。

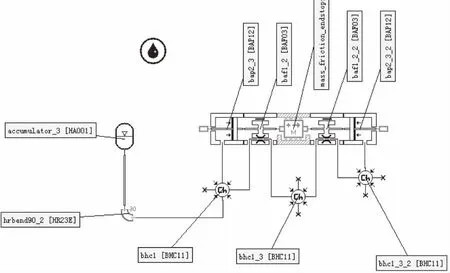
图1 AMESim仿真模型原理图

表3 关键元件参数设定

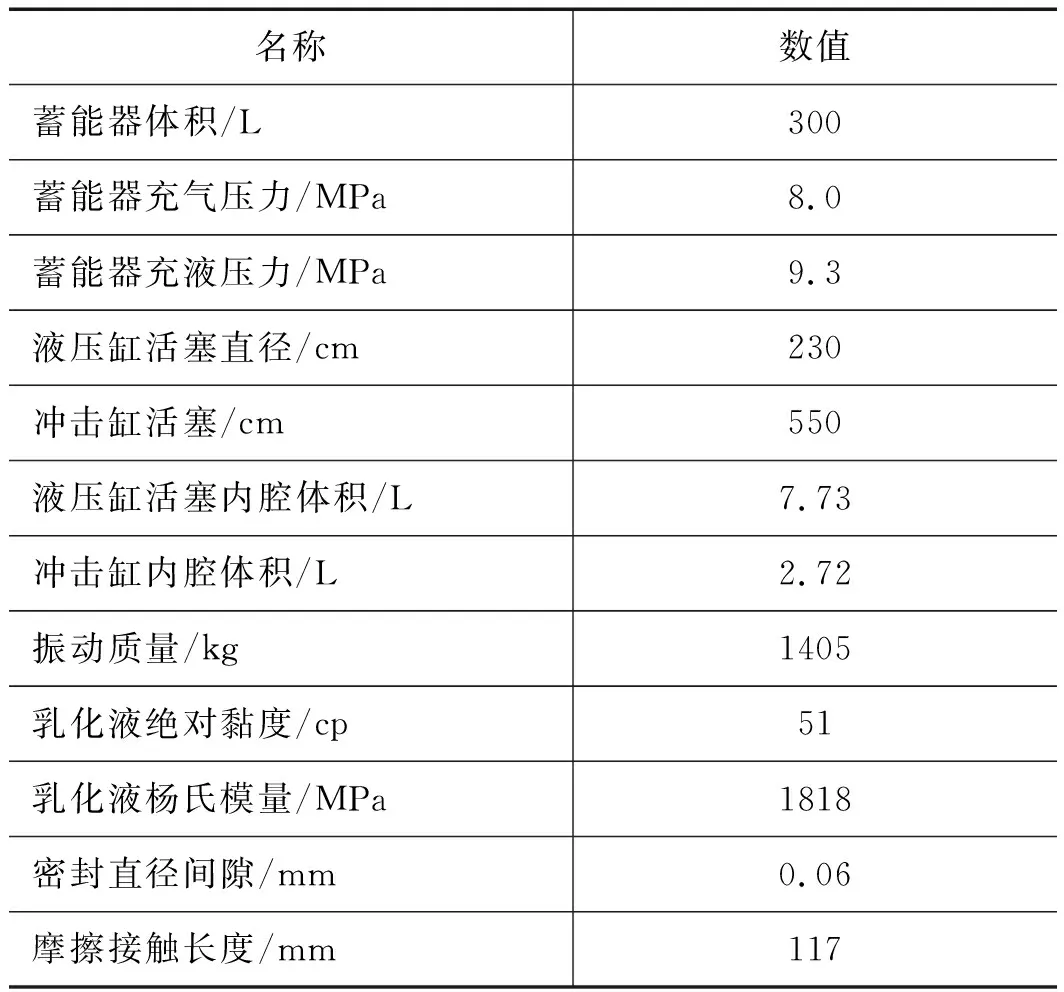
名称数值蓄能器体积/L300蓄能器充气压力/MPa8.0蓄能器充液压力/MPa9.3液压缸活塞直径/cm230冲击缸活塞/cm550液压缸活塞内腔体积/L7.73冲击缸内腔体积/L2.72振动质量/kg1405乳化液绝对黏度/cp51乳化液杨氏模量/MPa1818密封直径间隙/mm0.06摩擦接触长度/mm117

1.4 运行仿真

仿真运行起止时间0～0.5 s，采样时间间隔为0.0001 s，采用标准积分器，单精度计算。参数设置完毕后，运行仿真程序得到模拟计算结果。图2为仿真计算得出的1.5倍动载过载条件下的液压缸下腔压力 -时间曲线。

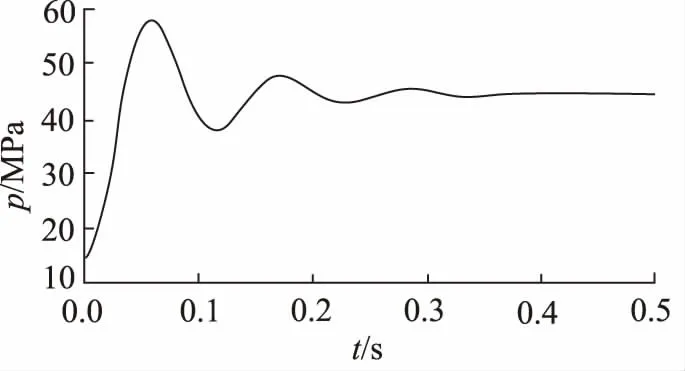
图2 液压缸下腔时间-压力曲线图(1.5倍动载)

2 ANSYS workbench瞬态动力学仿真分析

利用AMESim仿真计算得出动载过载条件下液压缸下腔压力数据，将压力数据简化并导入workbench瞬态动力学仿真模型，对液压缸缸体及活塞杆进行有限元仿真分析，得出液压缸结构件在不同内腔压力下的应力应变分布规律。

2.1 搭建仿真模型

建立液压缸三维模型，导入workbench仿真软件，添加材料属性，液压缸结构件材料均选用27SiMn，液压缸模型剖视图如图3所示，材料属性如表4所示。

图3 液压缸模型图

表4 液压缸材料属性参数表

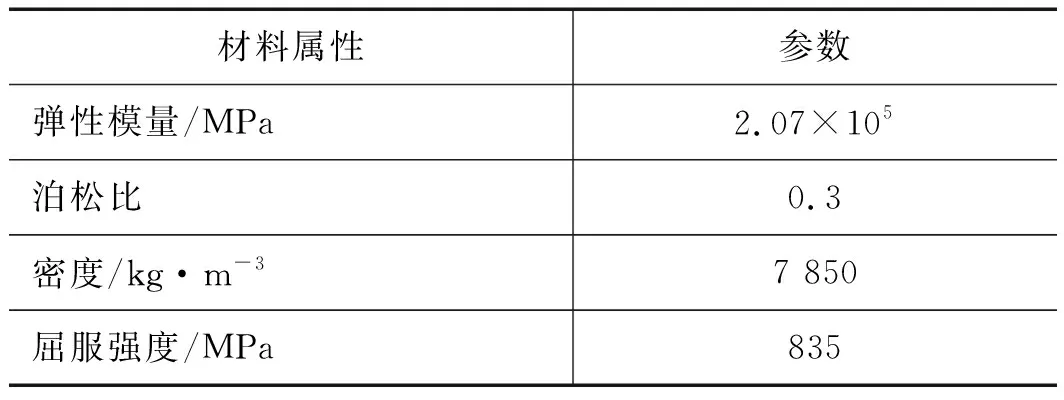
材料属性参数弹性模量/MPa2.07×105泊松比0.3 密度/kg·m-37 850屈服强度/MPa835

液压缸结构件接触定义：由于冲击时间较短，冲击瞬间假设液压缸各结构件没有发生相对位移，导向套与缸筒、活塞与缸筒内壁、活塞杆与导向套接触面均定义为bonded。

2.2 载荷施加及约束

(1) 在动载过载条件下，液压缸下腔内部封闭且充满高压液体，忽略其泄漏及活塞与缸筒、导向套与活塞摩擦。在有限元仿真环境下对液压缸下腔压力波动进行理想假设，液压缸下腔压力在同一时间点均匀分布，以1.5倍动载过载仿真计算为例，压力载荷施加时间步如图4所示。

图4 载荷施加时间步

(2) 约束方式：忽略冲击加载过程中活塞杆头部、缸筒底面的微小位移，在缸体底部曲面以及液压缸活塞杆头部表面添加固定约束。图5为施加载荷以及约束条件图。

图5 载荷及约束条件

2.3 加载及求解

运用ANSYS workbench仿真程序对液压缸进行动载加载，进行求解，得出缸筒、活塞杆应力应变分布情况仿真分析结果。1.5倍额定压力动载过载条件下，应力云图如图6所示。缸筒、活柱结构件最大应力-时间的关系曲线如图7、图8所示。

图6 活塞杆及缸筒应力云图(1.5压力倍率)

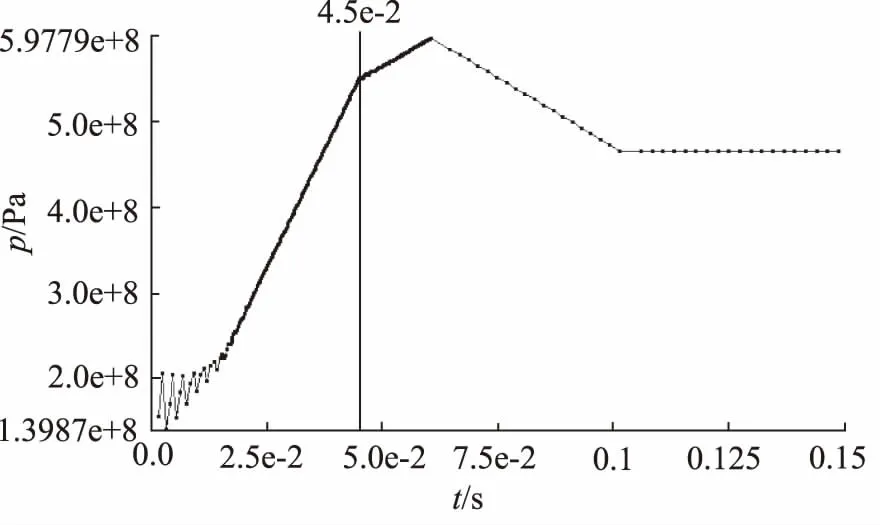
图7 活塞杆最大应力-时间曲线图(1.5压力倍率)

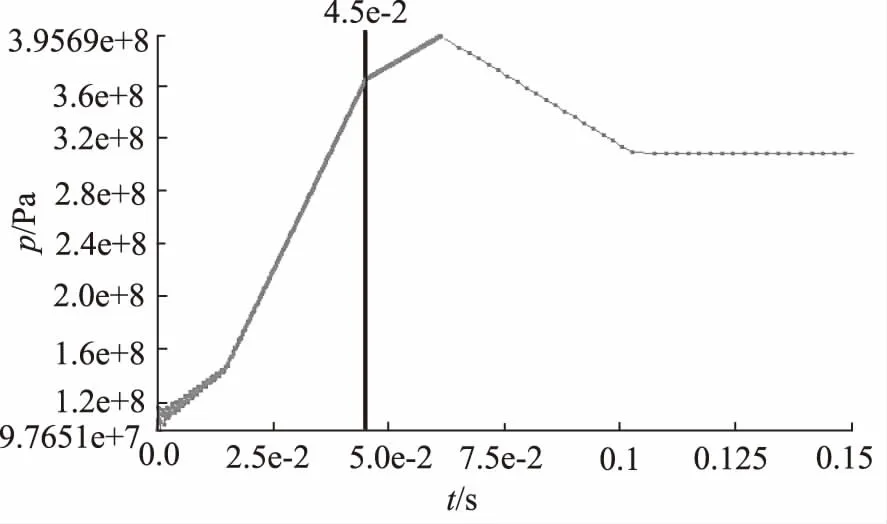
图8 缸筒最大应力-时间曲线图(1.5压力倍率)

3 试验研究

3.1 试验条件

6000 kN液压支架液压缸冲击试验台以蓄能冲击形式提供试验动力。数据采集处理方面，采用奥地利DEWESoft动态应力应变测试分析系统[16]。

3.2 测点布置及桥路设置

试验选用三向直角应变片，测点布置如图9所示。试验顺序按照压力由低到高依次进行，分别进行1.0～1.5倍率下的动载过载测试试验。

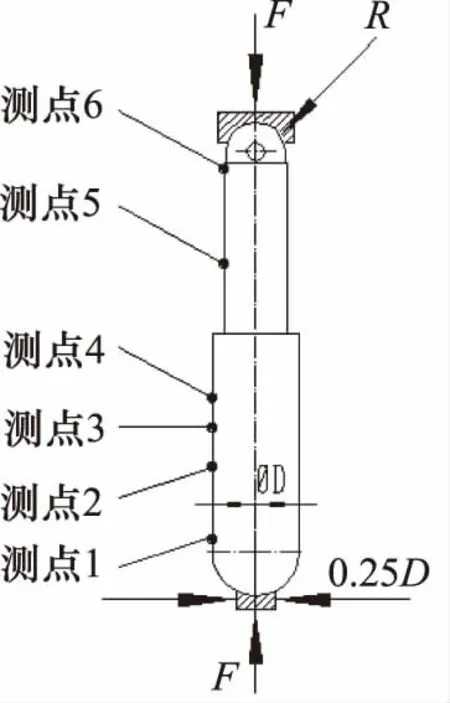
图9 测点布置图

3.3 采集数据处理

在动载过载冲击过程中，液压缸结构件最大应力点的分布位置与撞击后的时间长度有关。本研究选取测试数据为时间-压力曲线上，下腔压力达到0.6倍额定压力(即21 MPa)为时间起点，取第30 ms时对应的压力及应变值，进行处理分析。图10为测试软件采集到的液压缸下腔压力-时间曲线。

图10 1.5倍动载过载条件下的压力-时间曲线

通过应变花3个方向测得的数值计算主应力、主应变，其计算公式如下[17]：

主应变：

(1)

主应力：

(2)

εi为测点的单向应变值，E为材料的弹性模量2.06×105MPa,μ为泊松比取为0.3。

3.4 测试数据

对试验数据进行梳理，得到不同倍率下各个测点的主应力分布如图11所示。

图11 各测点不同倍率下的主应力

4 仿真分析与试验测试对比

4.1 AMESim仿真与试验结果比对分析

在6组不同倍率下的液压缸下腔压力-时间曲线中，分别取5个参量： 第30 ms压力、峰值压力、上升至压力峰值所需时间、波谷压力值、波峰到波谷时间长度(压力曲线时间起点取压力为21 MPa时的对应点)。针对上述参量进行6组仿真计算与试验数据的比对分析，如图12～图16所示。

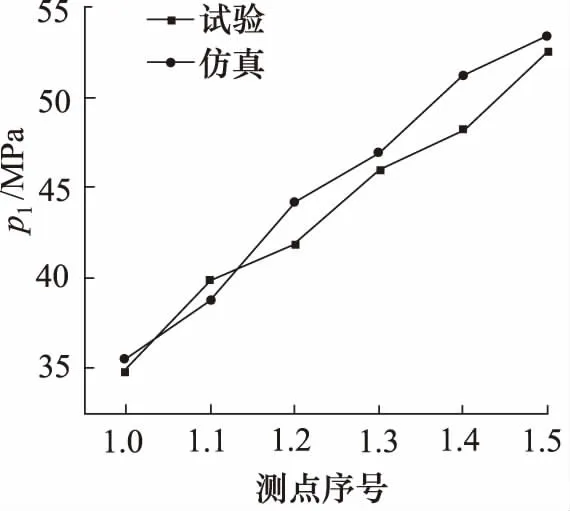
图12 第30 ms压力比对图

可以看出：仿真分析与测试试验得到的液压缸下腔压力-时间曲线基本吻合，其主要区别在于AMESim仿真环境下，波峰到波谷所需时间参量差异较大，最大误差45.4%；原因分析为：AMESim仿真环境中，忽略了现场试验条件下蓄能器与冲击缸连接管路内的压力损失；液压缸活塞与缸体摩擦、活塞杆与导向套摩擦产生的阻尼作用使用单个黏性摩擦及泄漏仿真元件BRF1进行模拟与实际试验环境下的阻尼有差别。因此导致液压缸内腔压力-时间曲线波形衰减与测试试验相比较为缓慢。

图13 峰值压力比对图

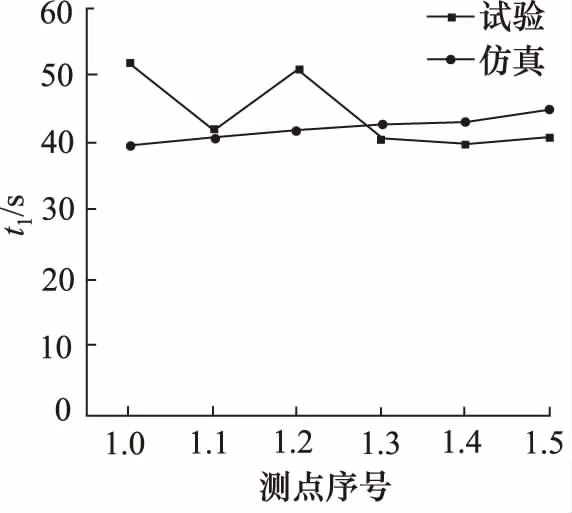
图14 上升至压力峰值所需时间比对图

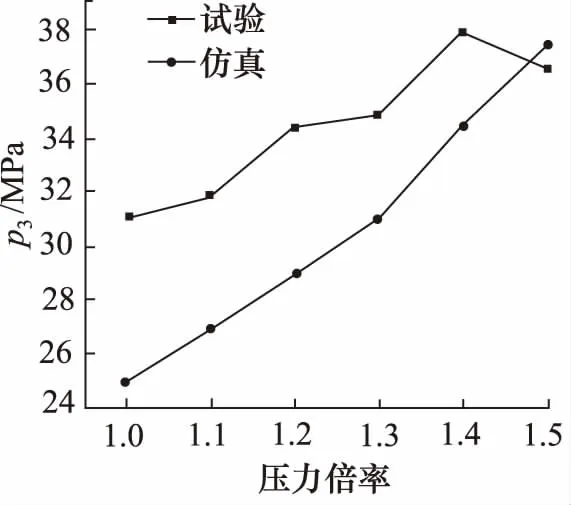
图15 压力波谷值比对图

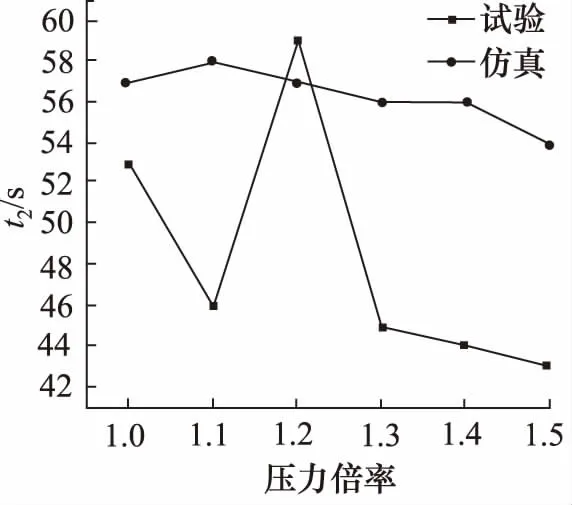
图16 波峰到波谷所需时间比对图

4.2 有限元仿真与试验比对

动载过载条件下，1.0倍，1.3倍，1.5倍压力倍率下的液压缸各测点主应力仿真计算结果与测试数据比对图如图17～图19所示。

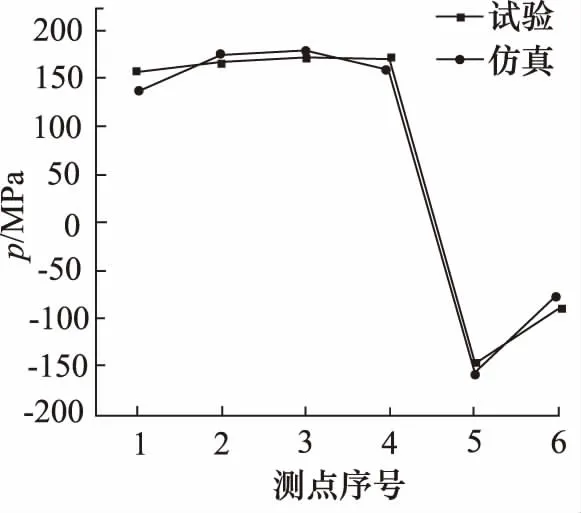
图17 1.0倍率下液压缸主应力比对图

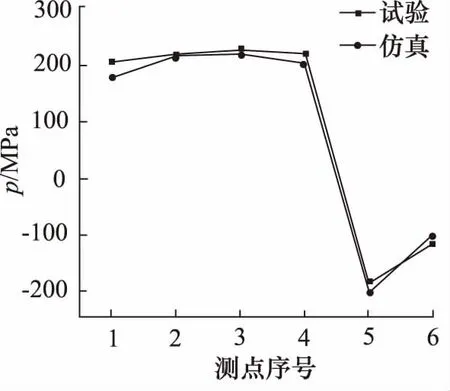
图18 1.3倍率下液压缸主应力比对图

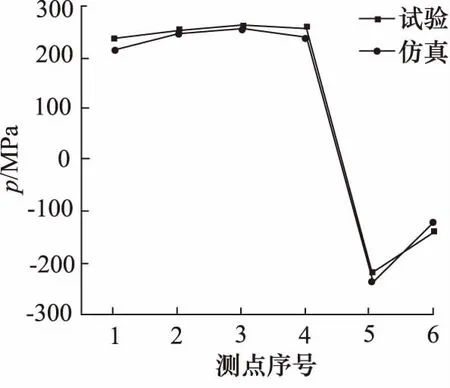
图19 1.5倍率下液压缸主应力比对图

分析上图可知：

(1) 有限元分析计算结果基本吻合与测试试验数据，最大误差15.5%。误差原因分析：现场试验过程中应变片自身具有横向效应从而引起电阻片阻值变化，产生误差；应变片黏贴时胶层厚度以及贴片角度不完全相同引起的随机误差；

(2) 在液压缸轴向方向上，各测点的分布规律保持一致，最大应力位置为测点3，1.5倍压力条件下的对应应力值为267 MPa，但最大应力点分布位置存在较小差异：仿真计算最大点位于试验值最大点下方3 cm 左右，原因如下：ANSYS仿真环境下边界条件假定液压缸下腔压力在同一时间点下均匀分布，忽略了动载试验下液压缸下腔压力波动变化引起的误差；测点黏贴位置无法精准控制。

5 结论

(1) AMESim仿真以及workbench有限元仿真计算结果与试验测试数据基本吻合。证明仿真分析模型搭建成功，能较好的模拟动载加载实际工况，为动载荷作用下液压缸预期破坏位置及抗冲击液压缸的优化设计提供理论指导;

(2) 动载过载条件下，液压缸在轴向方向上的应力分布趋势：有液柱区域缸筒部分液柱中上方约1/6处对应部分应力最大，应力分布呈向上下两侧逐渐减小的趋势，缸底处应力最小；无液柱区域导向套处应力最小，头部销孔处应力最大，活塞下端面、活塞杆与活塞杆头部焊接过渡区下方也存在明显的高应力集中区域，活塞杆中部应力分布基本持平;

(3) 1.5倍动载过载条件下最大应力测点分布位置位于液压缸无杆腔液柱中上部对应的缸体位置，外表面应力值为267 MPa，内表面应力点为363 MPa；活塞杆最大应力点位于活塞杆头部销孔处,该处出现应力集中，最大应力值为548 MPa。液压缸整体应力值均未超过材料屈服强度835 MPa；

(4) 当液压缸结构件应力值小于材料屈服强度的时：液压缸结构件应力应变分布规律与动载载荷大小无关；

(5) 未进行高于液压缸缸筒材料屈服强度以上的破坏性动载试验，后续学者可针对高强度液压缸动载过载特性展开研究。