“留白”教学，助推深度学习发生

郑梅华

[摘 要]受传统教学思想的影响，多数教师在课堂教学中往往片面追求短、平、快的教学效果，导致学生的认知是肤浅的、表面的，难以实现深度学习。对此，教师在教学过程中要合理“留白”，给予学生充分思考的时间与空间，让学生自主去辩论、感悟、建构知识，使深度学习真正发生。

[关键词]数学教学;深度学习;思维

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2020）05-0091-02

要想使学生的深度学习发生，就要关注学生的认知、想象和思维。通过课堂教学“留白”，能让学生有所思考、有所探索，使学生在动脑筋，用思维融合知识中达到深度学习的效果。

一、“留白”引辩，提升思维

课堂教学中，当学生的看法不一致时，教师应注意延迟评价并适当“留白”，给学生充分思考与辩论的空间。这样有利于培养学生不盲从权威，基于自己正确的经验做出分析与判断，达到训练思维、提升能力的目的。

【教学片段1】教师在教学“角的初步认识”后，出示了一道“一张长方形纸，如果剪去1个角，还剩几个角？”练习题。

生1：还剩3个角。

生2：还剩4个角。

生3：4个角剪去1个角，应该是3个角，不可能是4个角，我认为只剩下1个角。

师：到底还剩下几个角？请你们先动手剪一剪。

生1：我是沿着长方形的对角线剪一刀，就剩下3个角（如图1）。

生2：我是沿着长方形的一个顶点朝对边剪一刀，就剩下4个角（如图2）。

生3：我是沿着长方形两个角弯曲地剪一刀，就剩下1个角（如图3）。

生4：我认为他们说得都有道理，因为题目没有规定要怎么剪。

师：是啊！思维决定你的想法，这几种想法都有道理。那这个图形（如图4）又有几个角呢？

生（不約而同）：这个图中只有1个角，因为角的两条边必须是“直”的。

在这个教学片段中，整个教学过程显得生动活泼、新颖有趣。学生通过辩论、操作、交流，既深化了对角的认识，又在思维碰撞中提升了思维能力。

二、“留白”解惑，感悟本质

学起于思，思源于疑。学生在学习中出现的质疑能有效反映学生的思维状态和对知识的理解程度。学生对新知提出质疑时，教师要给学生“留白”，提供感悟知识本质的机会，让深度学习真正发生。

【教学片段2】教师在教学“3的倍数特征”时，引导学生借助数位顺序表摆小棒并交流想法。

生1：我在数位顺序表上摆了“18”这个数，十位上摆了1根小棒，个位上摆了8根小棒，总共用了9根小棒，9、18都是3的倍数。

生2：我在数位顺序表上摆了“24”这个数，总共用6根小棒，6是3的倍数，24一定也是3的倍数。

师（对第二个学生的表述提出质疑）：如果摆“123”这个数呢？它同样也是3的倍数吗？

生2：摆“123”这个数总共用6根小棒，因为6是3的倍数，所以123也是3的倍数。

师：3的倍数有什么特征呢？

生2：各位上的数的和是3的倍数，这个数就是3的倍数。

生3：我不同意他的看法，因为相同数位上的数才能相加，比如24中的“2”表示2个十，“4”表示4个一，2与4不能相加。

师：小组进行研究，或画图分析，或利用小棒分一分，看不同数位上的数能不能相加。

（学生操作，教师巡视）

生4：我们小组利用小棒分，先把18分成10和8，10根小棒里3根3根地分还余下1根，1根和8根合起来是9根，9根如果3根3根地分正好分完。我们发现余下的这个“1”不是1个十，而是1个一。

生5：我们小组是画格子，先把24分成20和4，20个格子3格3格地分还余2格，2格和4格合起来是6格，6格再3格3格地分正好分完。我们发现余下的这个“2”不是2个十，而是2个一。

师：那判断123这个数是不是3的倍数，你们用到的“1+2+3”又是怎么回事？

生6：因为123十位和百位上的数3个3个地分，余下的数字刚好和它对应数位上的数字相同。

当学生质疑“2个十不能与4个一相加”时，教师没有直接告诉学生为什么能相加，而是让学生自主操作感悟。学生在动手过程中就明白了“为什么判断一个数是不是3的倍数要看各个数位上的和”这个核心问题，从而实现了深度学习。

三、“留白”纠错，沟通联系

课堂教学中，学生难免会生成错误资源，教师要把这些错误资源当作宝贵资源，顺着学生的思维让学生示错，这样才能让学生纠正错误认知，沟通知识之间的联系。

【教学片段3】题目：王大爷准备用12根1米长的篱笆，一面靠墙围一个长方形或正方形的鸡舍，怎么围鸡舍的面积最大？

生1：用12÷3=4（米）得到鸡舍的边长，再用4×4=16（平方米）得到的就是鸡舍的面积。

生2：我同意他的方法，因为周长不变，围成正方形的面积最大。

生3：我也是这么认为的。

师：真的是这样吗？小组利用小棒动手围一围，并把各种情况记录下来。（学生活动，教师巡视）

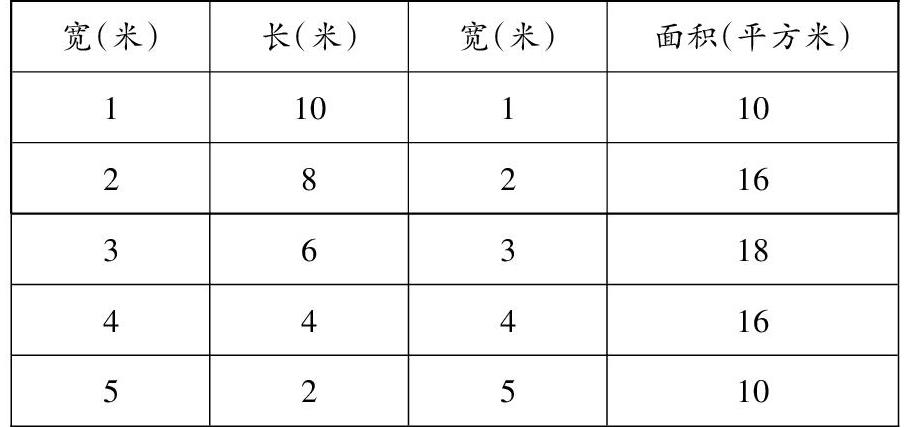
生4（展示记录表）：通过列表，我发现长6米、宽3米，围成的长方形面积最大。

[宽（米） 长（米） 宽（米） 面积（平方米） 1 10 1 10 2 8 2 16 3 6 3 18 4 4 4 16 5 2 5 10 ]

生5：我发现当长是宽的2倍时，围成的长方形面积最大。

生6：应该是围成正方形的面积最大，这一题怎么不是呢？

师：以前我们围的图形是四条边，而今天靠墙围的图形是三条边。我们先来观察这个图，它像谁的一半？

生7：在这个图形上面加一个一模一样的图形就是一个正方形，它是正方形的一半。

生9：周长相等时，围成正方形面积最大。围半个图形时，正方形的一半最大，即长是宽的2倍。

学生因为利用之前探索规律得到的结论“周长相等时，围成正方形面积最大”来解决靠墙围鸡舍的问题，出现了集体性的错误。这时教师不是急于告诉学生答案 ，而是通过“真的是这样吗？”“通过操作，你们有什么发现？”“这究竟是为什么？”等问题，充分发挥“留白”作用，鼓励学生自主探索并发现“用四条边围图形”与“用三条边围图形”的关系，沟通了知识之间的联系，实现了深度学习。

总之，数学课堂是思维的课堂，学生是学习的主人，教师要适时“留白”，为学生搭建表述观点、解惑释疑、示错纠错的平台，只有学生有了思维的土壤，深度学习之花才能如期盛开。

（责编 覃小慧）