火灾下钢框架耐火极限有限元分析

米琳琳 姜 静 张瀚天

（1.牡丹江大学建筑工程学院，黑龙江 牡丹江 157011；2.佳木斯大学建筑工程学院，黑龙江 佳木斯 154000）

1 前言

钢结构是当今建筑业的热点之一，随着钢结构的广泛应用，国内外关于钢结构抗火失效的例子也随之增多，给人民生命和社会财产造成巨大损失。钢材虽不是可燃材料但其导热系数大，在火灾作用下力学性能显著改变，使承载能力变弱，所以耐火性差是钢材最主要缺点。近年来许多学者对钢框架构件、节点等高温后力学性能进行了研究，[1]-[4]得出的结果为钢结构抗火设计提供了依据。本文应用有限元软件建立三层三跨钢框架结构，研究六个房间受火后温度场分布、柱横向位移、梁挠度变化。目的是得到钢框架耐火时间和临界温度，为钢结构防火设计提供参考。

2 有限元方法及验证

本文应用有限元软件ABAQUS，模拟文献[5]中单层钢框架火灾试验，模型见图1。模型参数与试验相同，温度按ISO-834标准升温曲线加载。模拟选择顺序耦合，即先进行热分析再把热分析结果导入力学模型中进行力学分析。在热分析中，钢材和混凝土的热工性能按T.T.Lie[6]给出的参数选取，受火构件表面热对流系数取25W/m2，热 辐 射 取0.85W/m2，Stefan-Boltzmann常 数σ=5.67×10-8W/（m2·k4）。

试验测点如图2所示，从图3～图5中可看出模拟结果与试验结果趋势上吻合较好，说明ABAQUS软件模拟的可行性。图3、图4中测点试验温度高于模拟温度，随着时间推移温度差越来越小，最大误差33%。误差原因是试验初始温度高于室温，在试验过程中试验炉内采用燃油点燃喷火装置，虽然升温采用的是ISO-834升温曲线，但炉内温度仍是高于升温曲线。柱顶侧向位移误差25%，造成误差的原因主要是模拟与试验的温度误差导致产生的应力大小不同，此外钢材含碳量、构件初始缺陷等也影响结果。

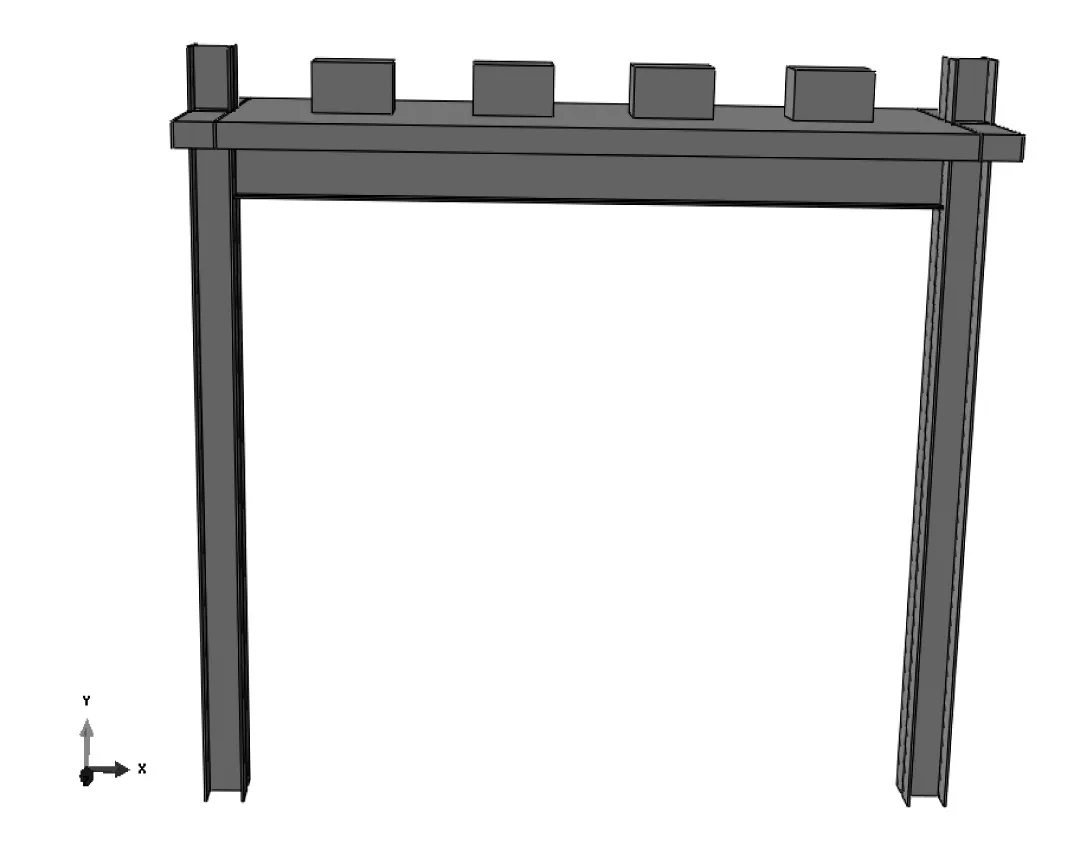
图1 单层钢框架模型

图3 柱测点温度-时间曲线对比

图4 梁测点温度-时间曲线对比

图2 柱和梁测点位置图

图5 钢框架柱顶侧向位移-温度曲线对比

3 火灾下三层三跨钢框架有限元分析

建立三层三跨钢框架结构，层高2.8m，跨度3.6m。梁、柱尺寸分别为H250×125×6×9和H200×200×8×12，均为Q235钢，柱线刚度大于梁线刚度，满足抗震要求。柱顶部作用有轴心荷载，外侧柱荷载100kN，内侧柱荷载180KN，所有横梁受均布荷载作用25kN/m，所有柱脚固定。假设材料为理想弹塑性体，钢材容重7850kg/m3，初始弹性模量2.06×105MPa，泊松比0.3，屈服强度均为290MPa。高温下钢材的导热、比热以及热膨胀系数均按欧洲规范EC3[7]和EC4[8]取值。

为研究火灾下钢框架耐火时间和临界温度，假设火灾分别发生在六个房间。由于梁上部有混凝土板，柱腹部有防火墙，为了与实际情况相符合，故钢梁三面受火，上部不受火，钢柱一面受火。计算时，不考虑火源具体位置，假设同一截面上温度相等。初始温度为20℃，按ISO-834标准升温曲线加载，60s为一个载荷步，加热1500s。钢框架模型见图6。

火灾下，判断钢结构整体或钢构件达到极限承载力标准为：

（1）结构整体丧失稳定；

（2）受火梁跨中挠度f≥L/250（L为梁的跨度）；

（3）柱横向位移δ≥H/30（H为层高）。

本文梁破坏挠度f≥3600mm/250=14.4mm，柱横向破坏位移δ≥2800mm/30=93.33mm。

图6 钢框架模型

图7 梁、柱截面温度-时间曲线

3.1 温度场分析

受火房间在不同时刻的温度分布具有普遍规律，因此以一层边跨为例研究受火房间温度场分布。图7反映的是受火梁、柱翼缘与腹板的温度随时间变化的关系。可看出，梁温度总体上高于柱温度。梁腹板温度最高，下翼缘温度略低于腹板，这是因为梁三面受火，腹板同时受到热传导和热辐射的作用且腹板薄于翼缘。柱由内翼缘至外翼缘温度依次降低，柱腹板的防火墙充分起到了阻隔火势蔓延的作用，仅靠热传导作用外翼缘温度上升缓慢，最终温度仅为67℃。

3.2 变形分析

3.2.1 一层边跨与一层中跨变形分析

受火房间变形见图8、图9。由图10、图11可知钢框架受火后，随着温度的升高，梁、柱变形越来越大。

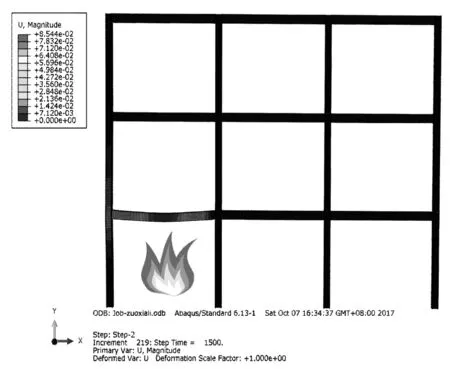
图8 一层边跨变形图

图9 一层中跨变形图

（1)一层边跨受火时梁在0s～1080s刚度下降使挠度缓慢增长，1080s～1140s强度显著降低使挠度突然增大，在1140s时挠度增大到19.79mm＞14.4mm，所以梁耐火极限时间是18min，临界温度743.10℃，梁构件失效。柱横向位移先在0s～1080s增大，后1080s～1500s减少，因为梁、柱受热膨胀使柱在X方向有位移，随着梁在Y方向的挠度不断增大对柱产生拉力，使得柱横向位移逐渐减小，而在整个受火过程中柱横向最大位移出现在梁柱节点处41.757mm＜93.33mm，整个钢框架并未失稳。

（2）一层中跨受火时梁在0s～900s挠度缓慢增长，900s～960s挠度突然增大，960s增大到17.043mm＞14.4mm，所以梁耐火极限时间是15min，临界温度708.877℃，梁构件破坏；柱横向位移在0s～900s逐步增长，900s～1500s逐渐减小，最大位移出现的时间晚于边跨且最大位移小于边跨，是因为中跨柱受两边结构轴向力约束作用，限制其在横向的发展。在整个受火过程中柱横向最大位移出现在梁柱节点处16.927mm＜93.33mm，整个钢框架保持稳定。

3.2.2 二层边跨与二层中跨变形分析

受火房间变形见图12、图13。由图14、图15可知：

图10 一层梁挠度-时间曲线

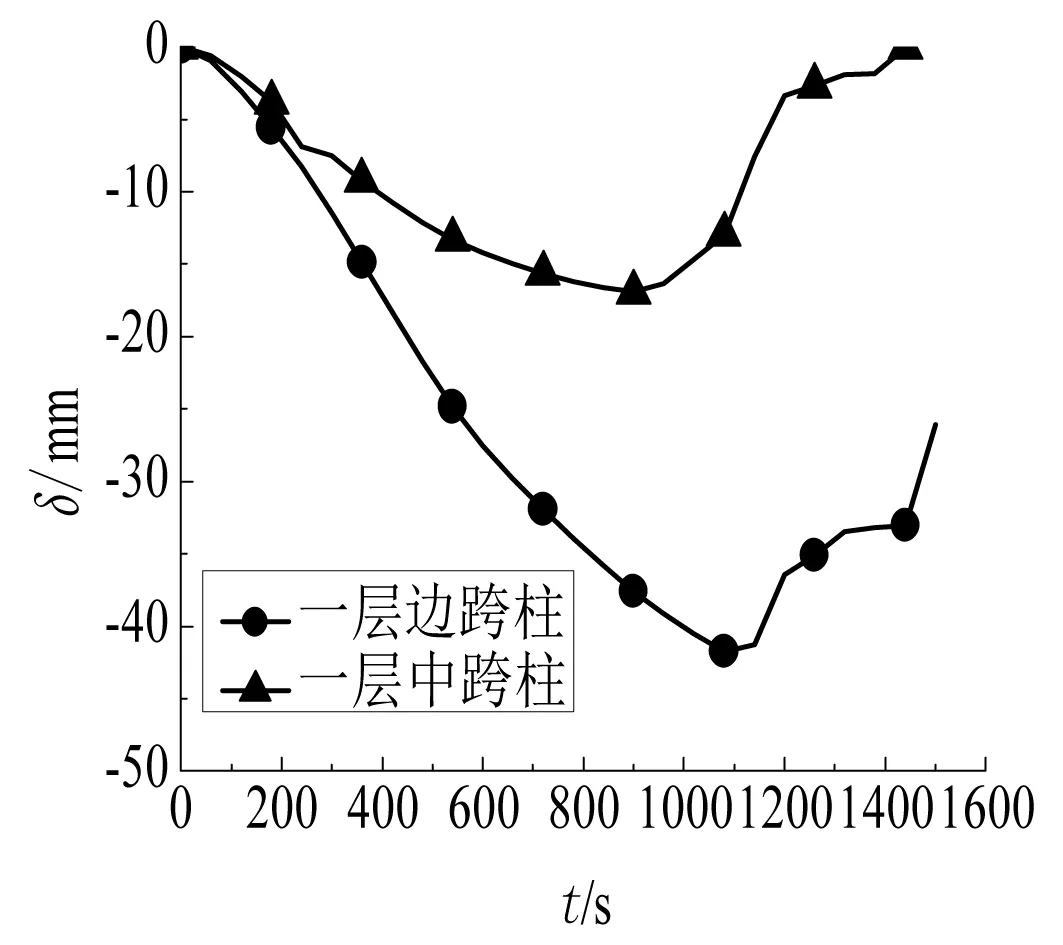
图11 一层柱横向位移-时间曲线

图12 二层边跨变形图

图13 二层中跨变形图

二层边跨受火时梁从0s～1080s挠度缓慢增长，1080s～1140s挠度突增，在1140s时挠度增大到17.295mm＞14.4mm，所以梁耐火极限时间是18min，临界温度741.46℃，梁构件失效；柱横向位移在0s~1080s增大，1080s～1500s减少，整个受火过程中柱横向最大位移40.635mm＜93.33mm，整个钢框架并未失稳。

二层中跨受火时梁从0s～1020s挠度缓慢增长，1020s～1080s挠度突然增大，增大到21.369mm＞14.4mm，所以梁耐火极限时间是17min，临界温度730.552℃，梁构件破坏；柱横向位移在0s～1020s逐步增长，1020s～1500s逐步减小，在整个受火过程中柱横向最大位移18.152mm＜93.33mm，整个钢框架仍然保持稳定。

图14 二层梁挠度-时间曲线

图15 二层柱横向位移-时间曲线

2.2.3 三层边跨与三层中跨变形分析

受火房间变形见图16、图17。由图18、图19可知：

（1）三层边跨受火时梁在外力作用下先有向下挠度，由于上部没有房间的约束作用，柱、梁受火膨胀，此时膨胀产生的向上位移大于外力产生的向下位移因此挠度向上，随着温度升高刚度、强度下降梁向下挠度不断增大，在1440s时挠度增大到21.559mm＞14.4mm，所以梁耐火极限时间是23min，临界温度792.01℃，梁构件失效；整个受火过程柱横向最大位移51.816mm＜93.33mm，整个钢框架并未失稳。

图16 三层边跨变形图

图17 三层中跨变形图

图18 三层梁挠度-时间曲线

图19 三层柱横向位移-时间曲线

（2）三层中跨受火时梁在1200s挠度增大到16.265mm＞14.4mm，所以梁耐火极限时间是19min，临界温度为752.303℃，梁构件破坏；柱横向最大位移20.853mm＜93.33mm，整个钢框架仍然保持稳定。

4 结论

（1）结合分析可知，不同房间发生火灾对整个结构影响不同。本文每层边跨耐火时间均长于中跨耐火时间。6个受火房间中，耐火时间最短的是底层中跨15min，应加强防火措施；耐火时间最长的是三层边跨23min。

（2）整个受火过程中，梁均先于柱破坏，需适当加强梁构件防火措施。

（3）三层边跨的边柱变形最大，由于上部及左（或右）侧没有任何约束作用，使得柱横向位移最大51.816mm，虽然没达到极限状态，但在抗火设计中为薄弱构件，需加强防火措施。