基于子带信号瞬时频率的特征提取及其在车型分类中的应用∗

陈建新 尹雪飞 陈克安

(1 西北工业大学电子信息学院 西安 710129)

(2 西北工业大学航海学院 西安 710072)

0 引言

近年来，随着我国经济的迅速发展，全社会的汽车拥有量增加，从而导致了一系列的交通问题，例如交通拥堵、交通事故。智能交通系统是缓解道路交通问题的有效方法，该系统能够合理地利用交通资源，实现现有交通网络的高效率运转和信息化管理。车型分类技术在智能交通系统中占据了重要的地位，正确地分类识别出车型对公路收费、交通监控指挥、车流量统计等方面有重大意义。目前，用于车辆检测的技术有很多，例如感应线圈、视频图像和微波等，它们都存在一定缺陷，感应线圈安装维护不方便；视频图像易受光线和遮挡物影响；微波技术主要用来检测而不是分类。车辆行驶时产生的噪声信号携带具有区分性的车型信息，可以用于车辆目标的分类识别。基于声信号的车型分类技术属于被动分类技术，具有隐蔽性高、安全性好、成本低和安装方便等优势。因此该技术受到国内外研究者的广泛关注。

实现该技术的关键之一是特征提取，目前声目标特征提取的研究主要包括两方面：一方面是基于信号处理方法分析其时频结构并从中提取有效特征，例如，Aljaafreh 等[1]使用基于频谱分布和小波包变换的方法提取特征用于车型分类；另一方面是鉴于人的听觉系统在听音辨物方面优势，从人对声音的听觉感知出发提取听觉特征，例如，陈克安等[2]使用基于Shamma 模型的听觉谱特性用于车辆目标识别。这些特征大多是基于信号幅度谱的，而忽略了信号相位信息的重要性，主要原因是在传统的语音信号处理中人们认为感知系统对相位不敏感，然而近年来随着研究的深入，发现相位信息在语音识别方面也是重要的。Nakagawa 等[3]通过联合Mel频率倒谱系数(Mel frequency cepstrum coefficient,MFCC)特征和相位信息提高了说话人识别的准确率，Paliwal 等[4]发现相位谱也能够像幅度谱一样对语音清晰度做出贡献。

鉴于此，本文利用相位的一阶导数瞬时频率(Instantaneous frequency,IF)来进行特征提取，使用耳蜗滤波器组将车辆噪声信号分解成子带信号，提出一种基于子带信号瞬时频率的特征提取方法，并将所提特征与对数能量结合，通过支持向量机(Support vector machine,SVM)进行分类识别，实验表明，本文算法性能良好，有一定应用价值。

1 实验数据

实验数据一共包括两个数据集。数据集1 来自DARPA /IXOs SensIT 项目的实验[5]，该数据包含两种军用车辆，即履带车(AAV)和重型轮式卡车(DW)的声波、地震波和红外波数据。文中选取声波数据进行车型分类实验，该声波数据的采样率为4960 Hz。为了保证实验的正确性，选取两类车型车次和采样点相同的数据，即AAV3∼AAV11 和DW3∼DW11的第51、52、53、54、55、56、58、59、60、61采样点，共180条数据，每条数据截取时长3 s，其中AAV5 和DW8 的 第53 采样点总时长只有1.5 s，分别用AAV3 的第42 采样点DW12 的第53 采样点代替。

数据集2 是通过自主实验采集到的数据，采集时间为2018年3月到6月，地点位于西北工业大学长安校区东大路，通过录音设备录制了公共汽车、小轿车、摩托车和卡车四种道路交通中常见车型行驶时产生的噪声信号。每类车型录制了120个样本，共480个样本，所有样本均是在单一车辆行驶经过的情况下收集的，采样频率为44.1 kHz，每条样本截取的时长为3 s，经分析发现，车辆噪声信号主要集中在低频范围，为了降低计算量，将样本采样频率降到16 kHz。为了方便实验描述，将上述四种车型分别记为A、B、C和D。

2 瞬时频率估计

瞬时频率估计比较常用的方法是希尔伯特变换法，该方法通过对信号进行希尔伯特变换求其解析信号，然后计算解析信号的瞬时幅度和相位信息，最后通过求解相位的一阶导数估计瞬时频率。

能量有限实信号s(t)的解析信号定义为

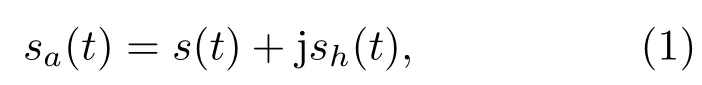
其中，sh(t)是信号s(t)的希尔伯特变换，通过Sh(w)的傅里叶反变换得到

解析信号sa(t)的极坐标表示形式如下：

其中，sa(t)和θ(t)分别是信号的幅度包络和解析相位，其中：

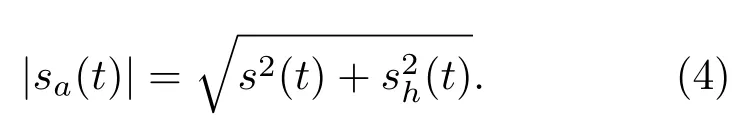
然后可以得到信号的瞬时相位：

通过对相位函数进行求导获得其瞬时频率：

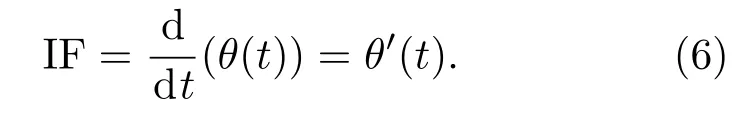
式(5)的相位角θ(t)存在相位卷绕问题，不能直接用于瞬时频率估计，需要将其展开，但相位展开算法通常是不准确的，因此会影响到瞬时频率估计。为了解决这个问题，使用傅里叶变换性质在没有显式求出θ(t)的情况下直接计算瞬时频率。

对式(3)两边同时取对数，并对时间求导数，可以得到如下式子：

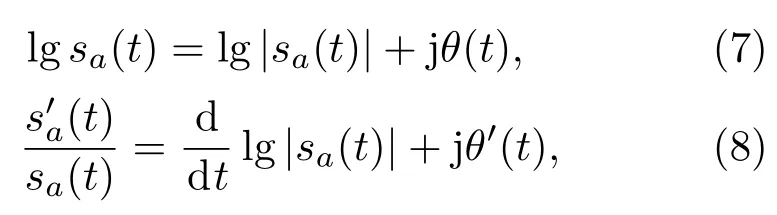
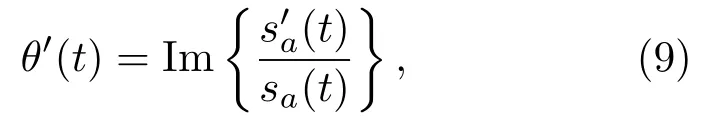
其中，Im{·}表示复数的虚部。可以用傅里叶变换的微分性质来计算解析信号的导数：

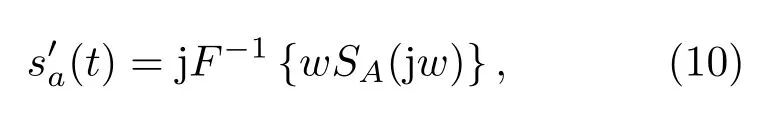
其中，F−1表示傅里叶反变换，SA(jw)是sa(t)的傅里叶变换，因此瞬时频率可以表示为

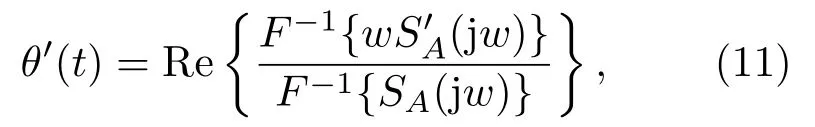
其中，Re{·}表示复数的实部。因为所使用的瞬时频率计算并不涉及到解析相位的计算，所以其不受相位卷绕的影响，性能更加稳定。

此外，为了进一步精确地表示子带信号的瞬时频率，通常进行瞬时幅度加权处理，这样能够使得瞬时频率的估计值在复杂情况下稳健性更好[6]，计算表达式如下：

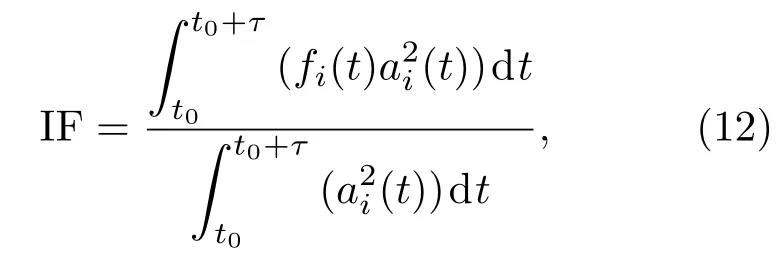
其中，τ为一帧信号的长度，t0为该帧信号的起始点，fi(t)为第i个子带信号的瞬时频率，ai(t)为第i个子带信号的瞬时幅度值。

3 特征提取

车辆噪声信号成分复杂，不能直接对其进行瞬时频率估计，需要将其分解成一系列的窄带信号，常用的做法是使用一组相互重叠的窄带滤波器组进行处理。本文使用能够模拟人听觉系统的耳蜗滤波器组[7]，相关研究发现，在耳蜗滤波器的每个中心频率中，从基底膜的底部到顶部，行波发生快速相位移动[8]，这种快速的相位变化可以通过其一阶导数瞬时频率来捕获，文献[9]证明了这一观点。此外，目前模拟耳蜗滤波的听觉模型主要用于研究其在不同中心频率下的幅度响应，虽然效果显著，但并不能完全等同于听觉系统对声音的处理过程，尤其是对相位的处理。因此研究了不同尺度下中心频率分布以及不同带宽下的耳蜗滤波器组对所提取特征性能的影响。

耳蜗滤波器的时域表达式定义为

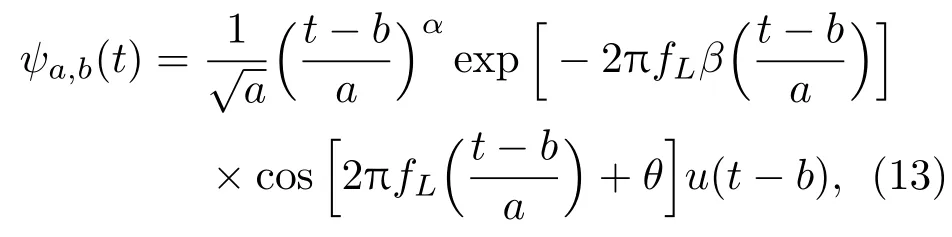
其中，α >0，β >0，用来确定耳蜗滤波器在频域中的形状和带宽，通常α取3，β取0.2或0.035；u(t)是单位阶跃函数，当t0 时，u(t)=1，否则，u(t)=0；θ值的选择应当满足ψ(t)dt=0；b是时移变量，a是尺度变量，a取值与耳蜗滤波器组的中心频率分布有关，定义为最低中心频率fl与当前中心频率fc的比值，即a=fl/fc。图1 显示了耳蜗滤波器组的幅频响应。

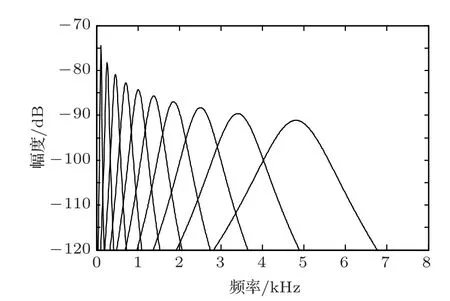
图1 耳蜗滤波器组的幅频响应(α=3,β =0.2)Fig.1 Amplitude frequency response of cochlear filter banks(α=3,β =0.2)

3.1 瞬时频率特征

使用耳蜗滤波器组提取瞬时频率特征的步骤如下：

(1)在分析频率范围内设计K个耳蜗滤波器，其中心频率分布为线性或非线性尺度。

(2)使用耳蜗滤波器组对车辆噪声信号滤波处理，一共获得K个子带信号，使用式(12)估计每个子带信号每帧的瞬时频率，假设一共分了N帧，那么就会获得一个K×N的矩阵。

(3)使用等效矩形带宽(Equivalent rectangular bandwidth,ERB)尺度压缩瞬时频率动态范围，该尺度的计算公式定义为fERB=21.4×lg(4.37×f/1000+1)，其中f为线性频率，fERB为压缩后的频率。

(4)使用离散余弦变换进行去相关和降维处理，将所提取的特征记为IF特征。

本文的分析频率范围为50 Hz∼fs/2，fs为最终采样频率，对于数据集1fs=4960 Hz，对于数据集2fs=16 kHz。滤波器的个数为40，特征维数为13。滤波器组的中心频率分布选择线性尺度和Mel尺度两种。

3.2 对数能量

信号的短时能量用来度量其幅值变化，定义为加窗声信号区域的振幅绝对值的平方和。其表达式如下：

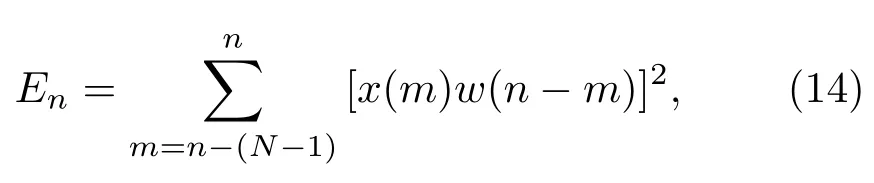
其中，En是短时能量，x(m)是待分析的车辆噪声信号，w(n)是窗函数，N是窗长。当窗函数为矩形窗时，短时能量描述如下：

本文在计算该值时选用矩形窗函数，考虑人的听觉特性，使用短时能量的自然对数ln(En)作为特征参数，并称之为对数能量[10]。

3.3 组合特征

使用瞬时频率特征和对数能量特征联合获得组合特征参数，主要具有两大优势：首先，对数能量从能量的角度描述车辆噪声信号，瞬时频率从相位的角度描述车辆噪声信号，两者具有互相补充作用；其次，对数能量作为标量值，不会引起特征维度过高而导致运算量过大问题。本文将瞬时频率特征和对数能量联合获得组合特征，计算每帧的对数能量作为该组合特征参数的第1 维特征，组合特征的维数为14。

4 特征评价

在进行目标识别时，要求所提取的特征尽可能区分各个模式类，希望其类内间距尽可能小，类间间距尽可能大。为了衡量本文所提取车辆噪声信号特征的优劣，援引文献[11]构造特征距离可分性测度：

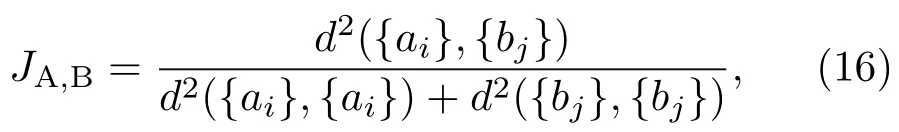
其中，d2(ai,bj)表示A 与B 的类间距离的平方，对应两类特征集合{ai,i=1,2,··· ,ka}和{bi,i=1,2,··· ,kb}，其中ai ∈A 类，bi ∈B 类，计算公式如下：

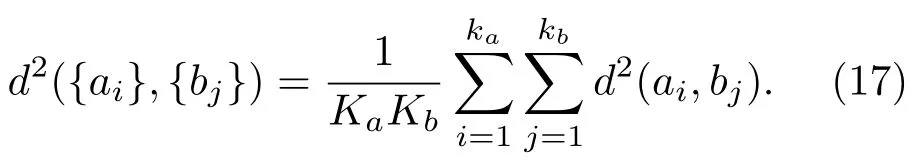
d2({ai},{ai})为类内距离的平方，对于某一类特征集合{ai,i=1,2,··· ,k},定义为

通常JA,B越大，类别间可分性越好；JA,B越小，其可分性越差。

耳蜗滤波器的带宽会影响到IF特征的提取，带宽过窄，会遗漏重要频率成分；带宽过宽，会影响到瞬时频率估计，如何选择合适的带宽是需要进一步研究的问题。根据上文描述，其带宽可以通过β值调节，β值通常取0.035 或0.2。本节通过实验来研究特征的可分性，其中IF 特征是在Mel 尺度下提取的。其可分性测度值如表1 和表2 所示。观察表1，可以看出随着β值的增加，IF特征对两种车型的可分性增加；观察表2，β为0.2 时IF 特征关于四种车型可分性测度值相对于β为0.035 时平均增加了0.0978(其中部分有所降低)。综合上面的实验结果，IF特征对车型的分类率与β值有关。

表3 和表4 显示了IF 特征和对数能量联合的可分性测度结果。对比表1 和表3，通过特征联合，两种车型的可分性测度值明显增加；对比表2 和表4，当β为0.035 时，四种车型的可分性测度值平均增加了0.1413，β为0.2 时，其可分性测度值平均增加0.2194(其中部分有所降低)。表明对数能量与IF特征联合可以增加车型的可分性。

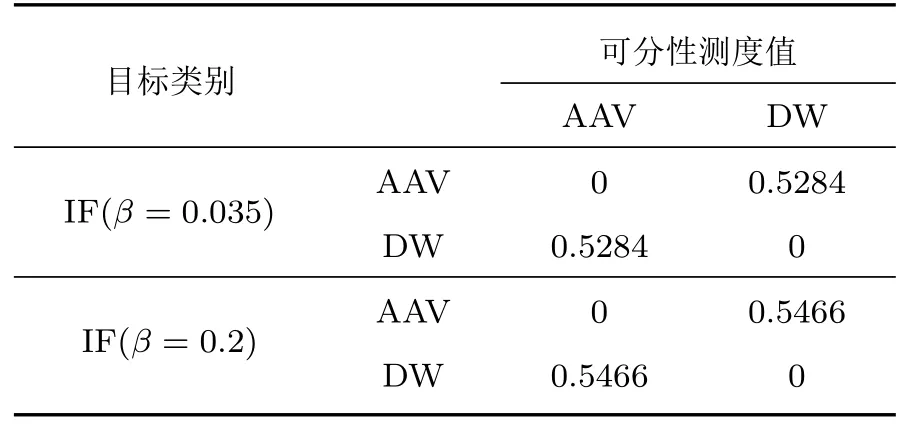
表1 IF 特征的可分性分析(数据集1)Table 1 Separability analysis of IF feature(Data Set 1)

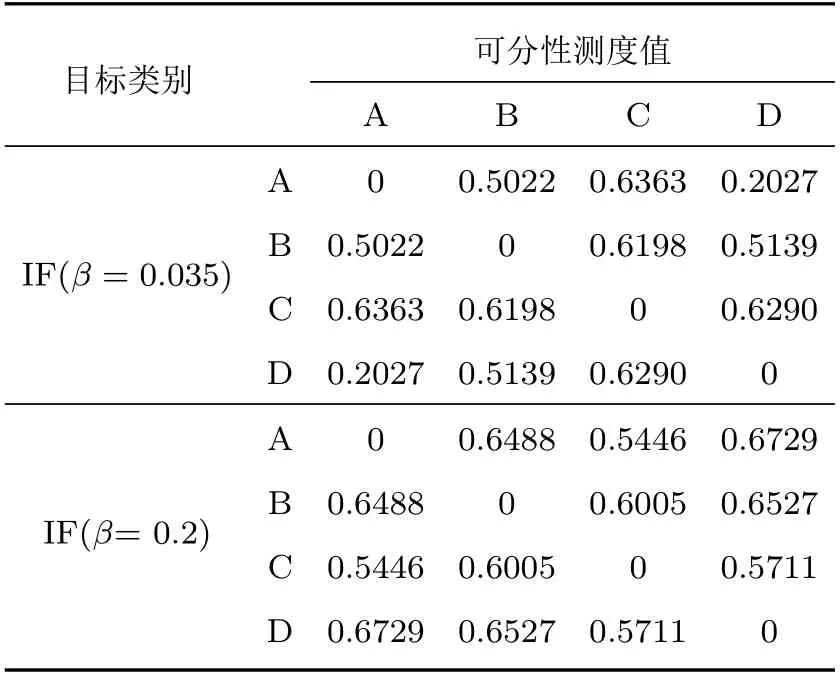
表2 IF 特征的可分性分析(数据集2)Table 2 Separability analysis of IF feature(Data Set 2)

表3 联合特征的可分性分析(数据集1)Table 3 Separability analysis of combination feature(Data Set 1)

表4 联合特征的可分性分析(数据集2)Table 4 Separability analysis of combination feature (Data Set 2)

5 实验仿真

支持向量机是基于结构风险最小化原则，适用于小样本、非线性、高维数和局部极小值点等实际问题，分类性能良好[12]，本文使用带有线性核函数的SVM 进行分类。实验时，每种车型取1/2 作为训练集，1/2作为测试集，取10次重复实验的平均值作为分类结果。

通过第4 节的特征评价实验表明IF 特征的分类性能会受到β值影响，取β等于0.035、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9、1.0，计算在线性尺度和Mel 尺度下所提取IF 特征对车型的分类能力。图2和图3 显示了耳蜗滤波器组取不同参数时的IF 特征分类结果。观察图2 和图3 可发现使用不同β值提取的IF 特征对车型进行分类时，其分类率先增加后减小，这验证了之前的分析，即耳蜗滤波器的带宽过宽或过窄都会影响子带信号的瞬时频率估计，只有选择合适的带宽才能提取性能更优的IF 特征。此外耳蜗滤波器组的中心频率分布同样会影响特征性能，Mel 尺度下的IF 特征对车型的分类能力明显高于线性尺度下的IF特征，主要原因是车辆噪声信号的有用信息集中在低频范围，而Mel 尺度在低频时分辨率高，因此性能更佳。当β为0.4 时，IF特征在数据集1 上关于线性尺度和Mel尺度上获得最高分类率分别为89.78%和91.56%，β为0.5时，IF特征在数据集2 上关于线性尺度和Mel尺度上获得最高分类率分别为79.58%和84.42%，表明该特征具有适应性，对不同数据集可以通过调节β值使其获得最高分类率。

图2 不同参数下的IF 特征分类性能对比图(数据集1)Fig.2 Comparison of IF feature classification performance under different parameters (Data Set 1)

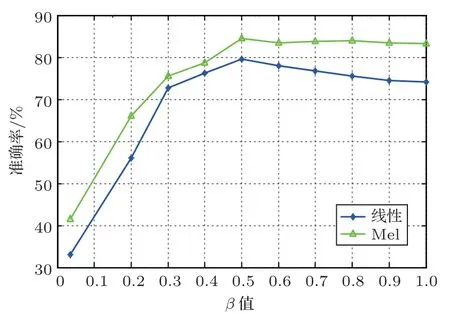
图3 不同参数下的IF 特征分类性能对比图(数据集2)Fig.3 Comparison of IF feature classification performance under different parameters (Data Set 2)

表5和表6显示了最高分类率下的IF特征及联合特征在两个数据集上的分类率。综合两个数据集上的实验结果，IF 特征与对数能量联合能够有效提高车型分类率，在两个数据集上大约有4%∼5%左右提升。为了进一步验证本文算法的有效性，比较了文献[13]和文献[14]的实验结果，本文算法均优于文献[14]的算法，虽然单一特征矢量相对文献[13]中的结果略差，但通过特征联合可以有效提升分类性能。此外值得注意的是，无论是本文的IF特征还是文献[13]和文献[14]中的两种分类方法对DW车型的分类率相对偏低，而本文提出的联合特征则能在提高总体分类率的前提下，缩小两种车型间分类准确率差异，使得车型DW 分类率接近AAV。

表5 IF 特征及联合特征的分类率(数据集1)Table 5 Classification accuracy of IF feature and combination feature (Data Set 1)(单位：%)

表6 IF 特征及联合特征的分类率(数据集2)Table 6 Classification accuracy of IF feature and combination feature (Data Set 2)(单位：%)

在实际应用中，车型识别容易受到噪声干扰，为了验证所提算法的抗噪性，使用文献[15]的方法提取13维MFCC特征进行对比实验。图4 和图5给出了Mel 尺度下的IF 特征及MFCC 特征在加入不同信噪比白噪声下的分类性能。从中可以看出IF(Mel)特征的分类性能在低信噪比下较差，在较高信噪比下分类性能普遍优于MFCC特征。在较强噪声存在的情况下，可以考虑在分类前端对车辆噪声信号进行降噪预处理操作以提高系统的噪声鲁棒性。

图4 不同信噪比下两种特征分类性能比较(数据集1)Fig.4 Comparison of two features classification performance under different signal to noise ratio(Data Set 1)

图5 不同信噪比下两种特征分类性能比较(数据集2)Fig.5 Comparison of two features classification performance under different signal to noise ratio(Data Set 2)

6 结论

在基于声信号的车型分类研究中，本文提出了一种基于耳蜗滤波器组的IF特征提取算法，并将该特征与对数能量相结合，通过可分性测度和分类实验表明所提取特征可以有效地实现车型分类并且抗噪性良好。本文实验也验证了相位信息同样能够反映声目标的重要信息，在声目标识别上有巨大应用潜力。