含平行裂缝储层中地震波频散、衰减及频变各向异性∗

郭俊鑫 方鑫定

(1 南方科技大学 深圳 518055)

(2 中国科学技术大学 合肥 230026)

0 引言

裂缝在碳酸盐岩及非常规页岩等油气藏中起到重要作用，是影响储层油气产量的关键因素。在碳酸盐岩储层中，受构造及成岩作用等影响，裂缝通常较为发育，其为油气聚集提供了空间，同时将储层中的孔、洞相连，对油气运移起关键作用[1−4]。对于非常规页岩油气藏，天然裂缝与压裂诱导缝极大提高了储层有效渗透率，其往往是油气运移的主要通道[5−8]。因此，对裂缝进行探测和表征是此类裂缝油气藏地震勘探的重要任务之一。由于裂缝尺度通常较小，难于从地震剖面上直接对裂缝进行识别和描述，故常利用地震属性对裂缝进行探测与表征。当地震波在裂缝储层中传播时，通常会发生明显的频散、衰减及频变各向异性[9−15]，故可利用这些地震属性进行裂缝探测。为此，首先需要理解地震波在裂缝储层中发生频散、衰减及频变各向异性的机制。

大量研究表明，当地震波在裂缝储层中传播时，主要的频散衰减与频变各向异性机制有两种，一种为地震波引起的流体相对于岩石骨架的运动，简称流体运动(Wave-induced fluid flow,WIFF)，另一种为地震波在裂缝表面产生的散射(Wave scattering)。本文首先将对这两种机制进行总结与回顾，在此基础上，针对前人研究的不足，本文将给出描述这两种机制的新模型并探讨这两种机制之间的耦合作用。由于在地壳应力作用下，裂缝往往呈平行排列，故本文仅考虑裂缝平行分布于储层中的情况。

0.1 流体运动机制

当地震波在饱和单相流体的裂缝储层中传播时，其特性可明显受裂缝性质及其与背景介质孔隙空间的连通性影响。这种影响是由裂缝与背景介质之间的流体运动导致的，其是一种与频率相关的现象[16]。在低频时，在地震波周期内，孔隙中的流体有充足的时间从裂缝流向背景介质或者从背景介质流向裂缝。相反地，在高频时，裂缝与背景介质中的流体没有充足时间进行运动。因此，裂缝在高频时较硬而在低频时较软。裂缝硬度随频率的变化导致裂缝岩石整体弹性性质随频率变化，即背景介质与裂缝中的流体运动导致地震波频散，并同时伴随由于孔隙流体黏性摩擦导致的能量耗散(地震衰减)。

裂缝与背景介质之间的流体运动导致的地震频散衰减可利用理论模型进行定量表征。针对此，目前已提出了一些相关的理论模型进行表征。Hudson 等[17]考察了单个硬币型裂缝与背景介质之间的流体运动(忽略相邻裂缝之间潜在的相互作用)。Chapman 等[18−19]通过在弹性非孔隙背景介质中引入圆孔与软裂隙，进而研究流体运动引起的地震频散与衰减。利用这一模型，Maultzsch等[10−11]与Chapman 等[20]分析了实验与地震数据，取得了良好的效果。除此之外，Jakobsen 等[21−23]利用T 矩阵的方法，在弹性背景介质中引入孔隙与裂缝，进而考察流体运动机制。这种方法具有较强的普适性，其能考察复杂裂缝分布的情况，但同时其需要较多的输入参数，而该类参数往往未知。

以上模型均是在弹性非孔隙背景介质中引入孔隙与裂缝，由于岩石往往本身为孔隙介质，所以另一类模型基于Biot 孔弹性理论直接在孔隙背景介质中引入裂缝。Gurevich[24]将裂缝作为孔隙背景介质的扰动，考察了低频极限下裂缝对岩石等效弹性性质的影响。Brajanovski 等[25]扩展了这一模型，其将裂缝等效成夹在孔隙背景介质中的高孔薄层，基于此得到了纵波频散衰减的解析表达式。同时，其还给出了频散衰减曲线在低、中、高频的渐近线及相应的特征频率[26]。类似地，Galvin 等[27−28]利用孔弹性理论分析了分布有稀疏硬币型平行裂缝的岩石中地震波的频散与衰减。Gurevich 等[29]利用分支函数的方法针对以上几种模型提出了统一模型。

0.2 散射机制

除了流体运动外，地震波在裂缝表面可发生弹性散射，同样可引起地震波的频散衰减与频变各向异性。针对这一机制，目前也已提出一些相关理论模型对其进行描述。Mal[30−31]研究了无限各向同性弹性介质中，纵波垂直入射到一个硬币型裂缝上时发生的散射。通过数值求解相应的积分方程，可获得裂缝附近及远端的应力与位移场。Martin[32]提出了一种解决线性边界值问题的新方法，据此研究了无限弹性固体中弹性波与硬币型干裂缝之间的相互作用。类似地，Krenk 等[33]、Keogh[34]及Martin 等[35]均对无限弹性介质中单个干裂缝的散射效应进行了研究。基于单个干裂缝的结果，根据Foldy 近似[36]可给出多裂缝分布下弹性波的散射频散、衰减及频变各向异性。Kikuchi[37]利用Foldy近似研究了含平行随机裂缝介质中波的散射衰减。Zhang 等[38]考虑了随机分布平行硬币型裂缝之间的相互作用，通过Foldy 近似给出了低频下波的散射频散衰减解析表达式。Zhang 等[39−40]还将这一结果推广到了全频率域范围内。对于2D 裂缝介质，Kawahara[41]研究了类似的问题。除了应用Foldy近似外，部分学者通过动态自洽理论等亦研究了平行裂缝分布下波的散射频散衰减[42−43]。

以上研究均假设裂缝为干裂缝，而在实际储层中，裂缝作为油气运移的重要通道，其往往充填有油气等流体。因此，有必要研究饱和流体裂缝的散射效应及引起的地震波频散衰减与频变各向异性。相对干裂缝的散射，对于饱和流体裂缝的散射的相关研究较少。Kawahara等[44]研究了饱和平行缝的散射，重点考察了黏滞摩擦对散射频散衰减的影响。Murai[45]对这一结果进行了扩展，考察了饱和裂缝之间的相互作用。除此之外，Sabina 等[46]及Smyshlyaev 等[42−43]利用动态自洽理论同样研究了饱和非黏性流体的随机分布硬币型裂缝的散射。Eriksson 等[47]利用T 矩阵和Foldy 近似的方法研究了相似的问题。

如上所述，虽然针对流体运动机制和散射机制，目前均提出了大量的理论模型来定量表征相应的地震波频散、衰减与频变各向异性，但是大部分模型均假设裂缝的厚度(即张开度)为无限小，可忽略不计。然而，在实际储层中，裂缝往往具有一定的厚度，裂缝厚度对裂缝的流体运输能力起重要作用，进而对储层整体渗透率影响重大。因此，研究裂缝厚度对地震波频散衰减与频变各向异性的影响对裂缝储层的地震勘探具有重要意义。针对此，本文作者及其合作者分别考察了裂缝厚度对流体运动机制与散射机制的影响，并建立了相应的理论模型。本文下面将对其进行重点介绍，最后将讨论两者的耦合作用。

1 流体运动模型

由于在实际储层中裂缝形态往往较为复杂，因此在建立流体运动模型时，通常将裂缝形态等效成软平面或者硬币型裂缝[29]。当裂缝半径远大于地震波长及裂缝之间的间距时，可将裂缝等效成软平面。这意味着裂缝可以用高孔薄层表示，这种裂缝一般称为平面缝(图1(a))。另一方面，当裂缝半径远大于或与裂缝之间的间距尺度相当，并且远大于孔隙尺度时，裂缝形态可近似为硬币型，其具有扁椭球体形态(图1(b))。针对具有这两种裂缝形态的岩石，本文作者及其合作者建立了统一模型，考察了裂缝厚度对地震波频散衰减的影响及相应的频变各向异性特征[48−49]。

图1 岩石裂缝形态的近似表征[48]Fig.1 Approximate representations of fracture shapes[48]

为了构建统一的理论模型，首先需要研究裂缝岩石在高频和低频极限下的等效弹性性质。下面将介绍求取高低频极限下裂缝岩石等效弹性性质的方法。

1.1 裂缝岩石高低频极限下等效弹性性质

为了求取裂缝岩石在高低频极限下的等效弹性性质，首先需要分析在高低频极限下的岩石物理状态。在低频极限下，裂缝中的流体有充足的时间与背景介质中的流体进行运动，因此流体压力在岩石当中保持平衡。这种情况下，可以利用各向异性Gassmann 方程来求取岩石的等效弹性性质。首先，可以利用线性滑动理论来求取干岩石的弹性性质[50]，进而可利用各向异性Gassmann方程对岩石进行饱和，从而求得饱和裂缝岩石在低频极限下的等效弹性性质。相反，在高频极限下，流体没有充足的时间在裂缝与背景介质之间进行流动从而导致裂缝中的流体与背景介质中的流体相互隔离。这种情况下，可以首先利用各向同性Gassmann 方程计算饱和背景介质的弹性性质，再利用线性滑动理论计算饱和背景介质中含干裂缝的岩石等效弹性性质，最后利用各向异性Gassmann 方程对裂缝进行饱和从而求取高频极限下饱和裂缝岩石的等效弹性性质。具体流程可参见文献[48]。

1.2 裂缝岩石中间频率下等效弹性性质

当频率在高低频极限之间时，岩石的等效弹性性质随频率变化。为了描述这一变化规律，Krzikalla等[51]及Galvin 等[52]提出岩石所有的弹性参数的驰豫函数应相同，即岩石的等效弹性性质可表示如下：

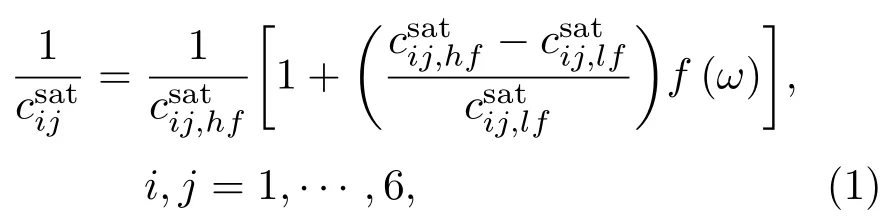
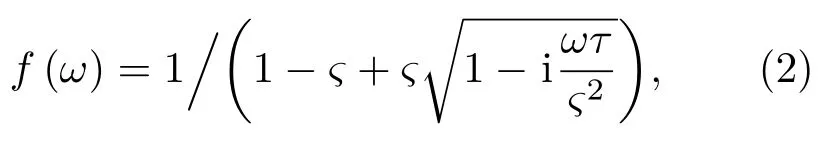
其中，ζ与τ决定了驰豫函数的形态，对于不同的裂缝形态，ζ与τ的表达式不同，具体可参见文献[48–49]。

对于单一驰豫函数的假设，理论上可解释如下：当地震波入射到裂缝表面时，裂缝与背景介质之间发生流体运动，其可看作一部分地震波能量转化为Biot慢波能量。当地震波频率远小于Biot特征频率时，慢波速度通常比入射波小两到三个数量级。根据Snell 定律，慢波的反射或透射角度将几乎垂直于裂缝平面，近似与入射波的入射角度无关。这意味着对于任意传播的地震波，流体总是沿着垂直于裂缝平面的方向流动。因此，对于所有的弹性系数，其应具有相同的驰豫函数。这一现象同样被数值模拟所证实，如Krzikall 等[51]、Lambert 等[53]及Rubino等[54]所做的研究。

除式(1)外，裂缝岩石的等效弹性性质也可用其柔度矩阵表示如下：

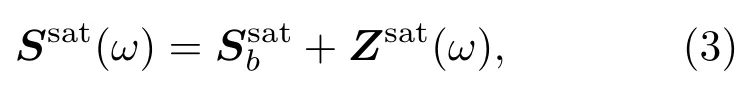
式(3)中，Ssat(ω)表示裂缝岩石随频率变化的柔度矩阵；表示饱和背景介质的柔度矩阵；Zsat(ω)表示随频率变化的裂缝柔度矩阵，其可表示如下：

式(4)中，ZT为裂缝切向柔度，为裂缝法向柔度，其随频率变化如下：

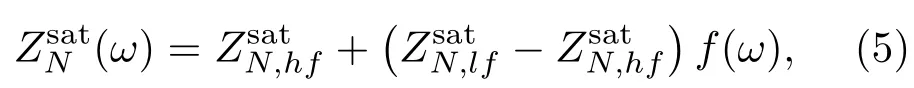
利用以上两种方法求取岩石的等效弹性性质后，即可计算地震波的速度频散与能量衰减，及频变各向异性特征[49]。需要注意的是，这里地震波的能量衰减采用品质因子的倒数(1/Q)表示，即单位波长内能量的衰减幅度表示，其与单位距离内能量的衰减幅度(地震波数的虚部)不同，其不随频率单调增大(由于单位距离内的波数随频率增大，因而单位距离内的衰减仍然随频率增大)。利用品质因子倒数易于分析地震波频散衰减的特征频率(即品质因子倒数峰值对应的频率)，且在地震数据的处理与解释中经常应用，故本文采取品质因子倒数表示地震波衰减，而不采用地震波数的虚部表示衰减。

1.3 数值算例

为了分析裂缝厚度对地震波频散衰减的影响与相应的频变各向异性特征，利用以上模型计算如下岩石中的地震响应。假设岩石背景介质渗透率较低为0.1 mD，孔隙度为0.1，岩石颗粒为石英，其体积模量为37 GPa，剪切模量为44 GPa，利用Krief 经验关系[55]可求得对应干燥背景介质体积模量为26 GPa，剪切模量为31 GPa[16]。裂缝长度为4 cm，裂缝厚度为0.06 cm，裂缝密度为0.06，干裂缝中有松软高孔填充物，其体积与剪切模量分别为0.04 GPa与0.02 GPa，填充物渗透率与孔隙度分别为100 D 与0.8；岩石整体饱含水，其体积模量与黏度分别为2.25 GPa与0.001 Pa·S。岩石结构示意图如图2所示。

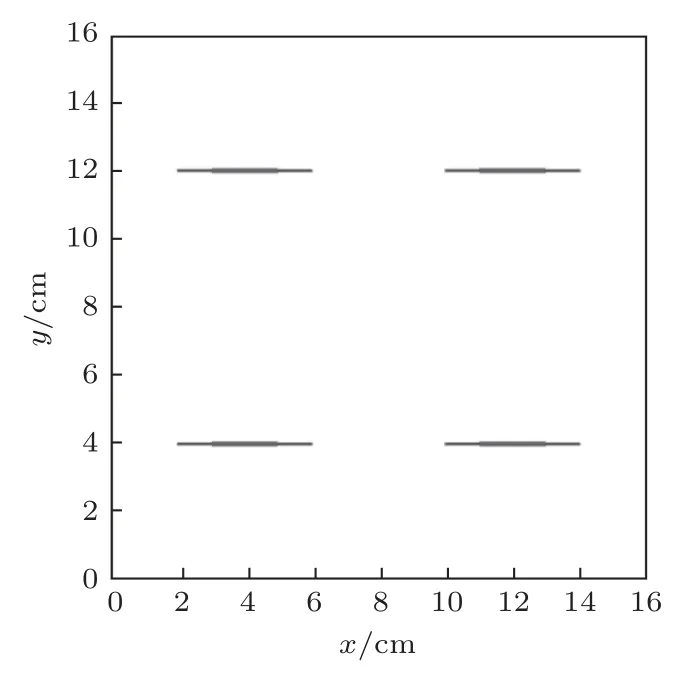
图2 含平行裂缝饱和岩石示意图[48]Fig.2 Saturated rock with aligned fractures[48]

利用给出的岩石参数，可以计算地震波在不同入射方向的频散衰减。这里首先考察纵波垂直入射于裂缝平面的情况。在这种情况下，纵波的频散衰减幅度一般最大，因此在此入射方向上便于考察裂缝厚度的影响。分别利用周期性平面缝分布、随机平面缝分布及随机硬币型裂缝分布三种模型(ζ与τ表达式不同，详见文献[48])，计算垂直于裂缝平面方向的纵波频散与衰减，同时也给出了周期性平面缝分布情况下解析解结果，如图3 所示。实线代表有限裂缝厚度的情况，为便于比较，图3 同样给出了裂缝厚度无限小的结果(如虚线所示)。

由图3 可看出，在流体运动机制的低频下(<10 Hz)，裂缝厚度对纵波的速度与衰减的影响很小，可忽略不计。但是在该机制的高频下(>10 Hz)，裂缝厚度对纵波的速度与衰减均有重要影响。有限裂缝厚度情况下(实线部分)纵波速度与衰减相对于无限小裂缝厚度情况下(虚线部分)明显减小。同时，纵波整体的频散幅度亦减小。由于流体运动机制的特征频率与背景介质渗透率成正比且这里所考察岩石的背景介质渗透率较低(0.1 mD)，因此地震频带处于该机制的较高频率区域，在此区域内可见裂缝厚度对频散衰减较为显著的影响，这表明对于低渗透率储层，地震波对裂缝厚度较为敏感，因而需要考虑裂缝厚度的影响。同时，地震响应对裂缝厚度的敏感性为地震探测裂缝厚度提供了可能性。

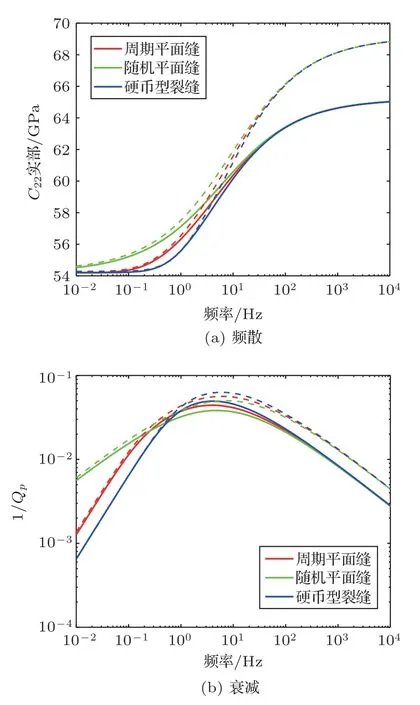
图3 垂直于裂缝平面纵波频散与衰减[48]Fig.3 Dispersion and attenuation of P-waves in the direction perpendicular to the fracture plane[48]

对于有限裂缝厚度情况下地震波频变各向异性特征，可以利用各向异性参数进行考察。对于速度各向异性，可以利用速度各向异性参数ε与δ表示，ε表示垂直与平行于裂缝表面两个方向上纵波速度的差异，而δ表示小入射角度下(以垂直于裂缝表面方向为零入射角度方向)纵波速度随入射角的变化率。对于衰减各向异性，可以利用衰减各向异性参数εQ与δQ表示，其含义与速度各向异性参数类似。ε与δ及εQ与δQ的具体表达式可参见文献[49]。图4给出了速度各向异性参数ε与δ及衰减各向异性参数εQ与δQ随频率变化的结果。虚线与星号分别代表利用式(1)与式(3)计算的弹性系数所得的各向异性参数，为了验证结果的准确性，同样给出了数值模拟结果(如实线所示)[54]。

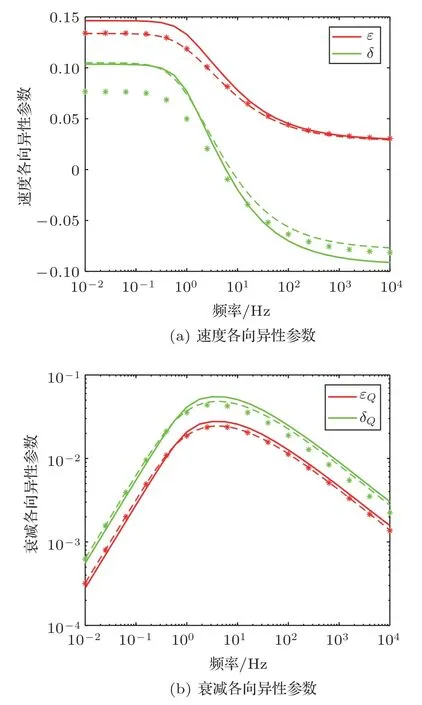
图4 速度各向异性参数与衰减各向异性参数随频率的变化[49]Fig.4 Variations of velocity and attenuation anisotropy parameters with frequency[49]

由图4可看出，对于速度各向异性参数，其随频率的增大而减小，ε逐渐减小到零，表明垂直与平行于裂缝表面的纵波速度趋于相等，而δ由正值逐渐变为负值，表明小入射角度下，地震波随入射角变化规律出现反转(由逐渐增大变为逐渐减小)。对于衰减各向异性参数，其在低频和高频极限下最小，而在特征频率处最大，表明衰减各向异性随频率先增大后减小。比较理论预测值(虚线与星号)与数值模拟结果(实线)可看出两者吻合良好，从而验证了理论模型的正确性。

2 散射模型

当裂缝尺度与地震波长相近时，除了裂缝与背景介质之间的流体运动引起的地震波频散衰减与频变各向异性外，地震波在裂缝表面亦会发生弹性散射，从而引起地震波的散射频散与衰减。这种现象在碳酸盐岩等裂缝储层中较为常见。因此，需要建立相应的理论模型对其进行表征。由于前人建立的模型大部分假设裂缝厚度无限小，故无法考察裂缝厚度对散射的影响。因此，本文作者及合作者建立了有限裂缝厚度情况下纵波的散射模型[56]。由于大裂缝一般侧向延伸较长，故模型仅考虑二维裂缝的情况，即裂缝在纵波入射平面内具有有限尺度，而在垂直于纵波入射平面的方向上无限延伸，裂缝随机分布在各向同性弹性背景介质中，如图5所示。

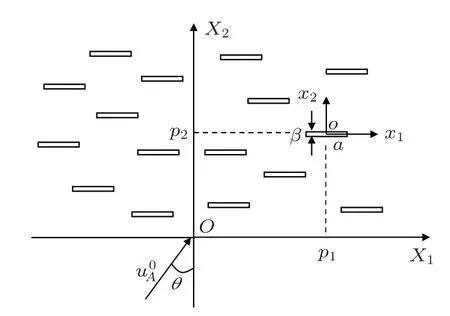
图5 纵波散射模型[56]Fig.5 Scattering model for P-waves[56]

2.1 模型推导

假设入射纵波位移场具有如下形式：

式(6)中，A0表示入射场振幅，kp代表入射纵波波数，θ代表入射角。

由于纵波在裂缝表面发生散射，散射场与入射场形成一个平均位移场，其可表示如下：

式(7)中，A代表平均场的初始振幅，κ表示散射对平均位移场的影响，利用κ即可求取等效纵波波数，进而获得等效纵波速度与衰减，故称κ为散射因子。

为了求取散射频散与衰减，必须求取散射因子κ，因此利用裂缝表面两侧法向与切向应力连续的边界条件，可建立如下积分方程[56]：其中，左侧代表背景介质一侧切向与法向应力，右侧代表裂缝一侧的相应值；D1与D2分别代表裂缝表面的切向与法向位移；T121(·)与T222(·)代表核函数；µ代表背景介质剪切模量；η与Kf分别代表裂缝中流体黏度与体积模量；β代表裂缝厚度。

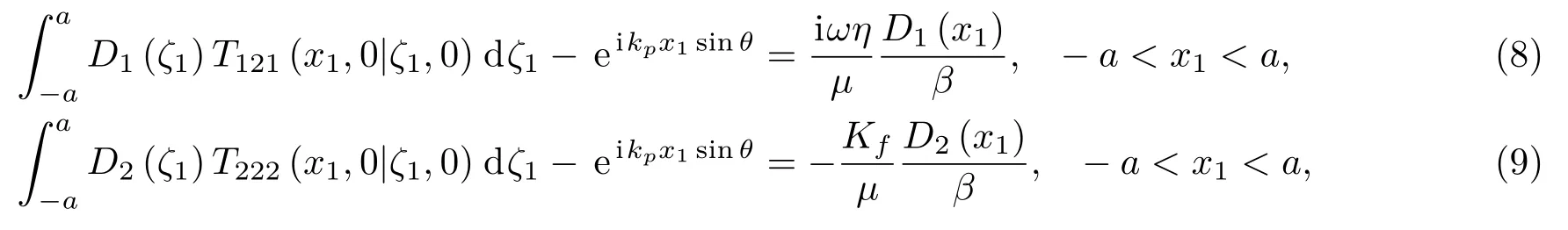
利用数值方法可求解式(8)与式(9)获得裂缝表面的切向与法向位移，进而可求得散射位移场强度如下：

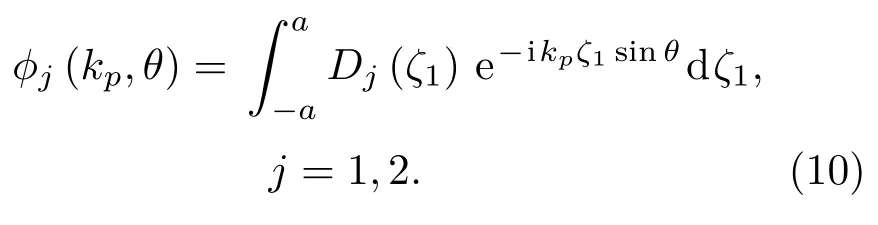
通过散射位移场强度即可求取散射因子，并进而获得纵波的散射频散与衰减：

具体模型推导过程可参见文献[56]。

2.2 数值算例

为了考察裂缝厚度对纵波散射频散衰减的影响，考虑如下参数：假设裂缝储层背景介质孔隙度可忽略不计，其体积模量为63.7 GPa，剪切模量为31.7 GPa，密度为2.70 g/cm3。背景介质中分布有平行排列的二维裂缝，其半径为20 m，裂缝密度为0.05。裂缝中饱含水，其体积模量为2.25 GPa，黏度为0.001 Pa·s。利用这些参数可计算纵波的散射频散与衰减，进而考察裂缝厚度的影响。与流体运动模型类似，当纵波垂直于裂缝平面入射时，产生的散射频散衰减通常最大，相应地，裂缝厚度的影响在这一方向上也应最大。因此，仅考察这一入射方向上裂缝厚度的影响，如图6 所示。注意裂缝厚度趋于无限小时，衰减趋于零，故在图6(b)对数坐标中无法显示。

由图6可看出，在低频时，裂缝厚度对纵波的散射频散与衰减均有重要影响，厚度越大，纵波速度越小，而衰减越大。随着频率的升高，裂缝厚度的影响减小，在高频下，裂缝厚度的影响可忽略不计。需要注意的是，不同于流体运动，这里低频指的是入射纵波的波长大于裂缝尺寸的情况，对于该组参数，裂缝厚度的影响在地震频带内最大。因此，对于分布有大尺度裂缝的储层，如碳酸盐岩储层，地震勘探中需要考虑裂缝厚度对地震波散射频散衰减的影响。反过来，根据裂缝厚度与地震波散射频散衰减的关系，可以开发相应的地震属性对裂缝厚度进行探测。

图6 裂缝厚度对纵波散射频散与衰减的影响[56]Fig.6 Influence of fracture thickness on the scattering dispersion and attenuation of P-waves[56]

2.3 实验对比

为了进一步分析裂缝厚度的影响，可将理论分析结果与实验数据进行对比，为此选取Wei 等[57]测量的超声实验数据进行分析比较。实验样品为分布有平行裂缝的人工样品，样品背景介质的体积模量为9.28 GPa，剪切模量为3.72 GPa，裂缝半径为1.5 mm，裂缝密度为0.083，不同样品具有不同的裂缝厚度(0.1∼0.34 mm)，裂缝中有近似流体的填充物，其体积模量为2.02 GPa。Wei 等测量了不同频率下垂直与平行于裂缝表面的纵波速度与衰减。利用上述参数可进行理论预测，并与实验结果进行对比，如图7 与图8 所示。图7 中星号和三角号分别代表垂直与平行于裂缝平面的纵波速度测量值，实线与虚线分别代表相应的理论预测值。图8 中星号代表测量结果，实线代表理论预测结果。两图中不同颜色代表不同的测量频率，绿色、蓝色、红色分别代表0.66 MHz、0.21 MHz及0.097 MHz。

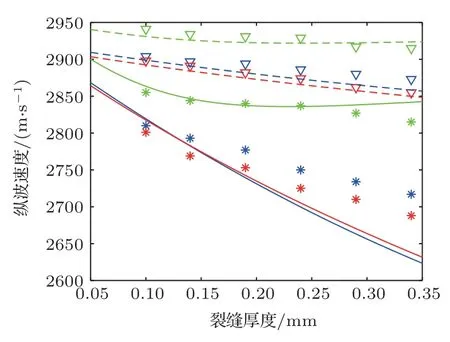
图7 纵波速度随裂缝厚度的变化[56]Fig.7 Variations of P-wave velocities with fracture thickness[56]

图8 纵波衰减随裂缝厚度的变化[56]Fig.8 Variations of P-wave attenuations with fracture thickness[56]

由图7 与图8 可看出，理论预测结果与实验测量结果总体吻合良好。速度随着裂缝厚度的增大而减小，而衰减随着裂缝厚度的增大而增大。低频下，裂缝厚度对纵波速度与衰减均有较大影响，而在高频下裂缝厚度的影响明显减小。上述结果进一步验证了裂缝厚度对地震波散射频散衰减的重要影响。

3 流体运动与散射机制的耦合

上面分别对裂缝储层中可能存在的两种地震波频散衰减及频变各向异性机制进行了研究与建模，重点考察了裂缝厚度的影响。在实际储层中，当两种机制的特征频率接近时，两种机制可能发生耦合，因此有必要对其耦合机制进行研究。对此，严格的理论考察可以从Biot 孔隙介质理论出发，结合相应的边界条件，可给出同时考虑流体运动与散射的地震波频散衰减与频变各向异性。这种方法较为复杂，这里给出一种简单的近似方法来考察两者之间的耦合[58]。对于流体运动，在低频时，裂缝中的流体与背景介质中的流体有充足的时间进行运动，从而导致裂缝的刚度变小，而在高频时，裂缝中的流体无法与背景介质中的流体进行运动，导致裂缝的刚度增大。这一效应可近似等效成裂缝中填充流体等效体积模量的变化，即利用频变裂缝流体体积模量来定量表征流体运动的影响。故可将该频变裂缝流体体积模量代入散射模型的边界条件得

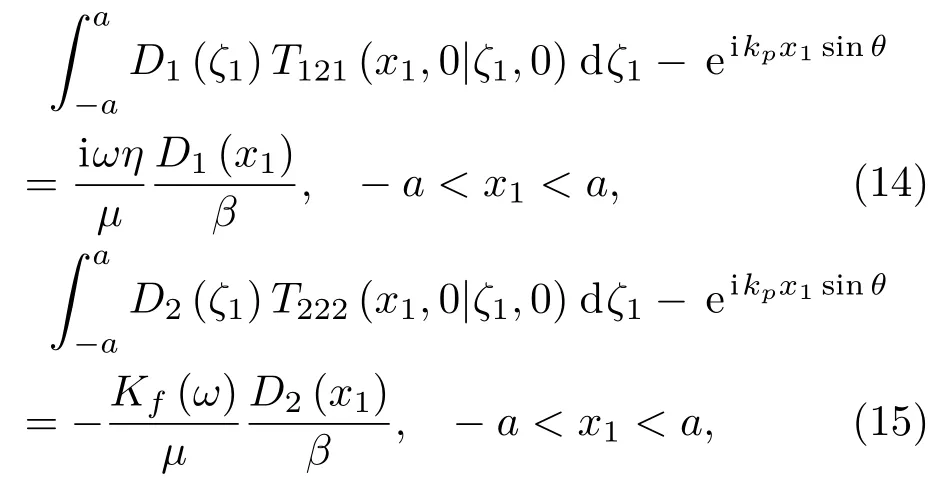
其中，Kf(ω)代表频变裂缝流体体积模量，其表达式可根据流体运动模型求出[58]。

将式(14)与式(15)结果代入式(10)∼(13)，可研究流体运动与散射的耦合机制。下面通过一个数值实例对两者的耦合作用进行分析。考察的样品骨架颗粒与干燥背景介质弹性性质与2.3节中相同，其他参数如下：背景介质孔隙度0.1，渗透率0.1 D；骨架颗粒密度2.65 g/cm3；二维裂缝长度30 mm，厚度4 mm，裂缝占整个岩石比例为0.0625，裂缝中充填有高孔物质，其体积模量为0.02 GPa，剪切模量为0.01 GPa，孔隙度为0.9，渗透率为10−9m2；背景介质与裂缝中均填充有水，其体积模量为2.25 GPa，黏度为0.001 Pa·s，密度为1.09 g/cm3，样品几何形态如图9所示。

图9 流体饱和裂缝孔隙岩石[58]Fig.9 Saturated porous and fractured rock[58]

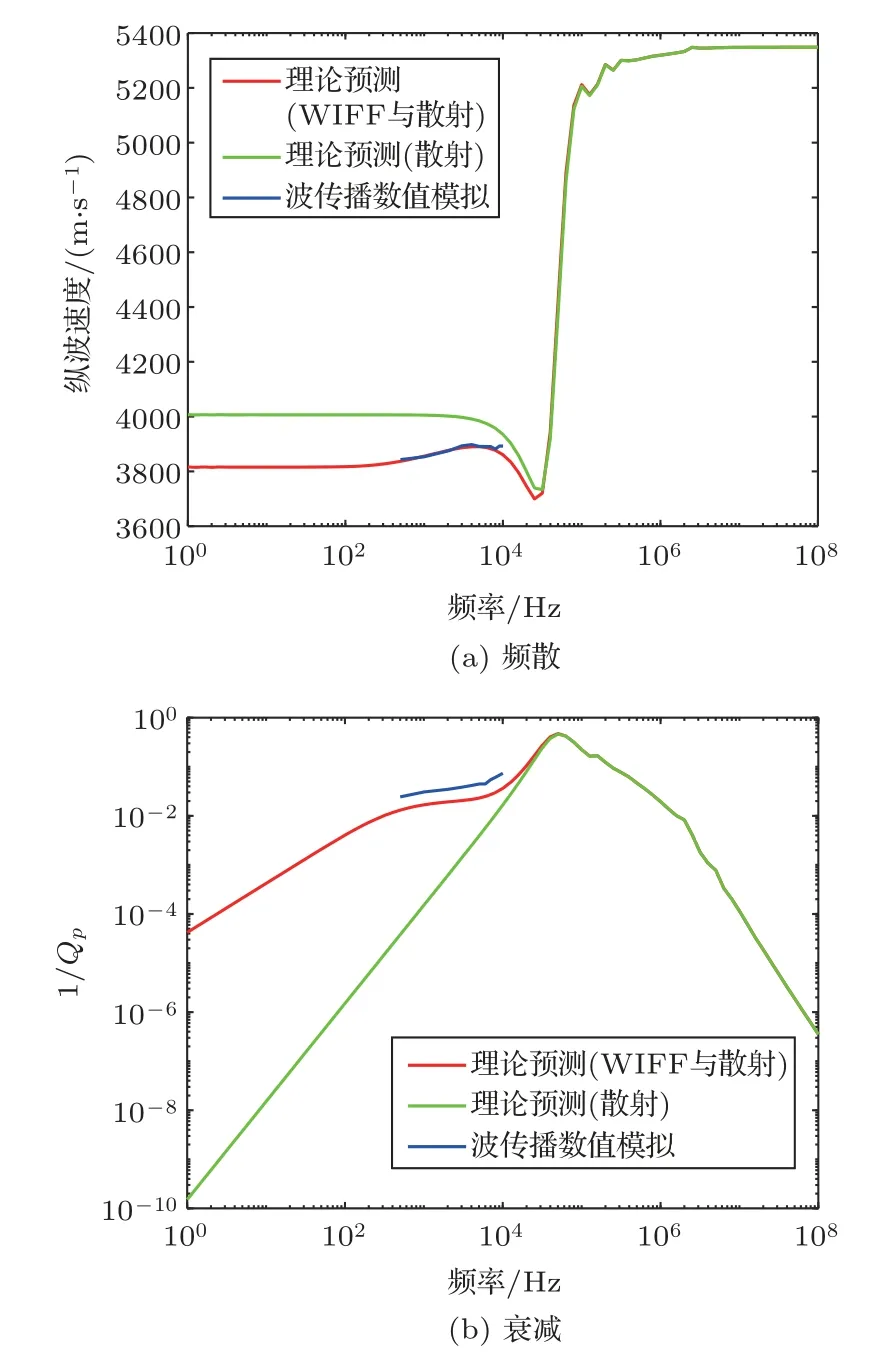
图10 垂直于裂缝平面纵波频散与衰减(同时考虑流体运动与散射机制)[58]Fig.10 Dispersion and attenuation of P-waves in the direction perpendicular to the fracture plane (considering both WIFF and scattering effects)[58]

利用上述参数可计算流体运动与散射同时作用下地震波的频散与衰减。由于在垂直于裂缝平面方向上地震波的频散衰减通常最大，故仅给出在该方向上的频散衰减，如图10 所示。为了验证理论分析结果，同时给出了仅考虑散射效应的结果及基于Biot 孔弹性理论的数值模拟结果。由图10 可看出，由于流体运动与散射机制的耦合，随着频率的增加，纵波速度先增大后减小，最后再迅速增大。这是由于在低频阶段，首先发生流体运动作用，导致速度增大，随着频率的增大，发生Rayleigh 散射使速度降低。当频率进一步增大时，发生Mie散射，从而使速度迅速增大。若不考虑流体运动作用，纵波速度在低频下将明显大于同时考虑两种作用的速度，而在高频下，由于流体运动作用的消失，仅考虑散射效应与同时考虑两种效应的结果趋于一致。对于纵波衰减，可以看出，当考虑流体运动与散射效应的耦合作用时，在低频下的衰减将明显大于仅考虑散射效应的衰减，并且衰减随频率的变化规律比单纯考虑一种机制时更为复杂，因此有必要考虑流体运动与散射效应的耦合作用。比较理论分析结果(红线)与数值模拟结果(蓝线)可看出两者所得速度基本重合，而数值模拟所得衰减略高于理论分析结果，其可能是由于理论分析未考虑样品界面透射损失所导致的。总体而言，理论分析结果与数值模拟结果吻合良好，其进一步表明了考察流体运动与散射耦合机制的重要意义。

4 结论

本文探讨了含平行裂缝储层中地震波发生频散衰减及频变各向异性的机理。针对裂缝储层中两种主要的频散衰减机理即流体运动与散射作用进行了重点分析。首先，对前人提出的理论模型进行了回顾与总结，在此基础上，针对前人未考虑裂缝厚度对地震波频散衰减及频变各向异性的影响的不足，本文作者及合作者提出了一系列理论模型对其影响进行考察。对于流体运动机制，考察了不同形态的有限厚度的裂缝，建立了统一模型，据此分析了裂缝厚度对流体运动机制的影响。结果表明，裂缝厚度在低频下影响较小，而在高频下影响较大。对于低渗透储层，高频区域可位于地震频带内，故需考虑裂缝厚度对地震响应的影响。对于散射机制，首先求取由有限厚度裂缝引起的散射场，进而根据散射场强度求取地震波散射频散衰减。结果表明，低频下裂缝厚度对散射频散衰减的影响较大，而在高频下影响较小。这一规律与流体运动机制正好相反。在实际储层中，流体运动机制的高频区域与散射机制的低频区域均较易发生在地震频带内，故裂缝厚度可对地震数据产生较大影响，应予以考虑，同时其为利用地震数据反演裂缝厚度提供了理论基础。裂缝厚度的探测可为储层有效渗透率等参数的预测提供重要信息，因此对于油气勘探开发具有重要意义。当流体运动机制与散射机制的特征频率相近时，两者可发生耦合，针对此，本文作者及合作者利用频变裂缝流体体积模量的方法对散射模型的边界条件进行改进，进而考察了两者的耦合作用。结果表明，当流体运动机制与散射机制发生耦合时，频散与衰减特征会发生明显变化，在实际应用中需要进行考虑。