基于黄金分割搜索算法的行波管测量方法

杨 垚 李 鋆 何元安

(1 哈尔滨工程大学水声工程学院 哈尔滨 150001)

(2 中国船舶工业系统工程研究院 北京 100036)

0 引言

水声材料作为水下声波产生、传播的重要介质，在我国海洋战略不断推进的今天，其重要性日益上升，因此，对水声材料声学参数的测量是水声材料研究的基础和关键。近年来，随着对水声材料的测试频率逐渐降低，模拟海洋环境条件下的各种水声材料及构件样品的声学性能测量需求越来越迫切。在试验室条件下，对声学材料小样的声学参数测量常在声管中进行，常见的声管包括脉冲管、行波管、驻波管[1]。

现有的行波场建立方法分为美国学者提出的传递矩阵法[2]与俄罗斯学者提出的迭代法[3]。中船重工第七一五研究所在“十五”期间建立了我国第一套行波管声管，采用迭代法进行主动消声，并通过对声速的校准提高了测量效果[4]。2010年，七一五研究所采用虚拟行波法进一步提高了测量的效果，据此实现行波管的单频及宽带测量[5]。2012年，中国船舶工业系统工程研究院也建成了行波管，采用迭代法进行行波场建立，在原来国内行波管的基础上提高了管内水听器的相幅一致性、信号采集的同步能力及信噪比，采用稀土型纵向换能器作为耐高静压的低频发射换能器，增强了发射换能器的低频声场稳定性。

现有行波场建立方法尚存在一定问题，传递矩阵法使用时需要对传递矩阵中各参数进行测量计算，测量精度将影响行波场建立效果；迭代法使用中需经过较长迭代时间后才可实现行波场建立。为了避免现有方法存在的问题，改善行波场建立效果，本文基于中国船舶工业系统工程研究院的行波管，设计了一种基于黄金分割搜索算法的行波环境建立方法，从而满足测量材料性能所需的环境，达到提升声管测试性能的目的。

1 算法说明

行波场建立通过有源吸声的方法，使用次发换能器发射抵消信号，令次发波形与主发波形经次发换能器反射面产生的反射波反相抵消，从而实现行波管的“半无限长”特性。

若输入至主发换能器的信号为x，声信号输入主发换能器发射，经过待测声学材料到达次发换能器反射面的传递函数为H主，入射至次发换能器反射面的声信号为P主，有

其中，∗表示卷积。假设P主到达次发换能器反射面产生反射声信号P反的传递函数为H反，有

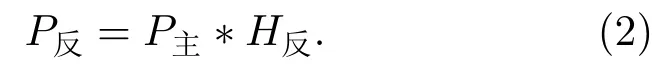
为了满足行波场建立的条件，次发换能器发射的声信号P次应满足P反=−P次的关系，综合以上各式可以得到P次为

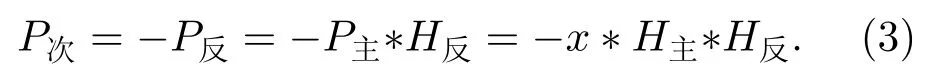
对式(3)取傅里叶变换，则有

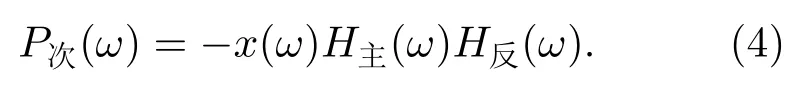
令输入至次发换能器的抵消声信号为x次，考虑信号输入至次发换能器发射声信号P次的传递函数为H次，有

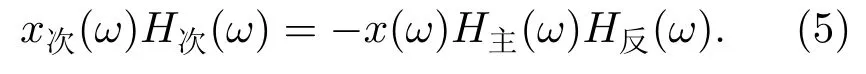
可解得

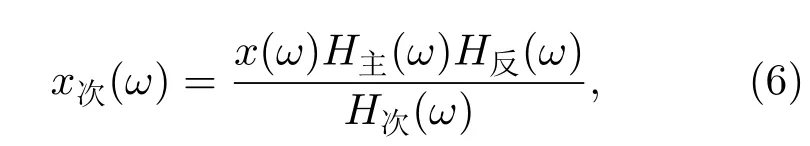
其中，若令x次(ω)=x(ω)Aejωτ时延，并令M(ω)ejφ(ω)可得

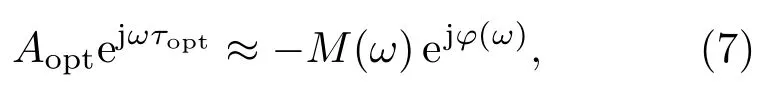
其中，M(ω)和φ(ω)分别为建立行波场所需的最佳幅度谱与相位谱，而Aopt与τopt为次发换能器发射时输入的最佳幅度与最佳时延。为了获得最佳的Aopt与τopt从而逼近M(ω)与φ(ω)以提高抵消效果，本文采用了一维黄金分割搜索算法用于搜索每一个测量频点的幅值A与时延τ时延，从而实现行波场的建立。

黄金分割算法通过以固定比率(即黄金分割率)减小搜索的范围，进而可以逼近区间内的极值点。在输入搜索时延或者幅值区间[a,b]后，由双水听器法得到此时的次发反射系数r1与r2，并在比较两者的大小后，令其中较大的一方按0.618 的黄金分割倍率缩小区间范围，然后开始新一轮的循环。当区间[a,b]的长度低于门限c之时，算法搜索完毕，具体流程如图1所示。

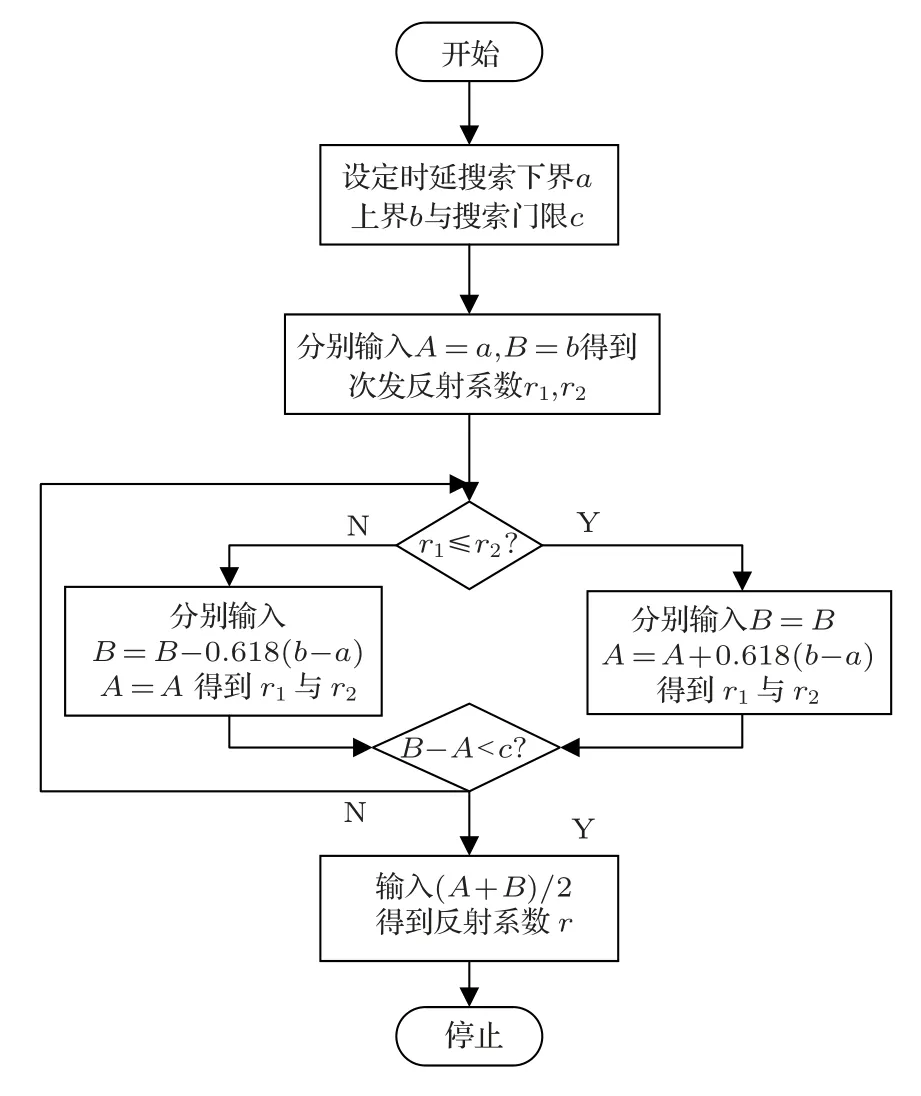
图1 黄金分割搜索算法原理框图Fig.1 Golden section search algorithm functional block diagram

令黄金分割率为Φ，则算法的搜索次数n与区间[a,b]及门限c关系如下：

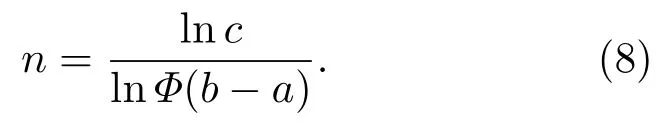
对于时延搜索而言，令fs为采样率，f为当前频点频率，且令搜索区间为当前频点下的半周期长的采样点数，门限宽度设置为1个采样点(即s)，则时延搜索次数n时延有

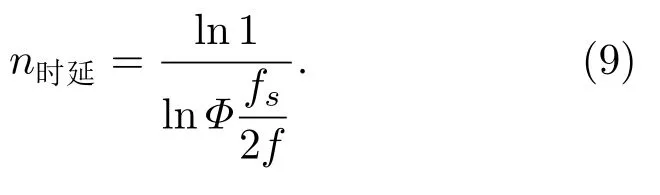
同理可得幅值搜索所需的次数。设置幅值搜索范围时需考虑功放输出许可范围，且由于行波场建立对时延更为敏感，故实践中可以略微放宽幅值搜索门限从而加快搜索次数。考虑到换能器的频响以及待测材料的声学特性，实践中应对每一测量频点进行幅值与时延搜索。

2 数值仿真

下面对使用黄金分割搜索算法建立行波场的方法进行数值仿真。建立如图2所示的行波管模型，使用主发换能器发射单频连续(Continuous wave,CW)正弦脉冲信号，该信号经由次发换能器界面反射，并使用次发换能器发射抵消信号对回波进行抵消，使用双水听器法对回波进行分离。图2 为数值仿真位置关系示意图，行波管长L=4.5 m，仿真中假设声信号在声管中的信道为纯时延信道，水听器的灵敏度为1，并假设两端换能器与外围电路的频响是由随机数组成的32 阶有限脉冲响应(Finite impulse response,FIR)滤波器。

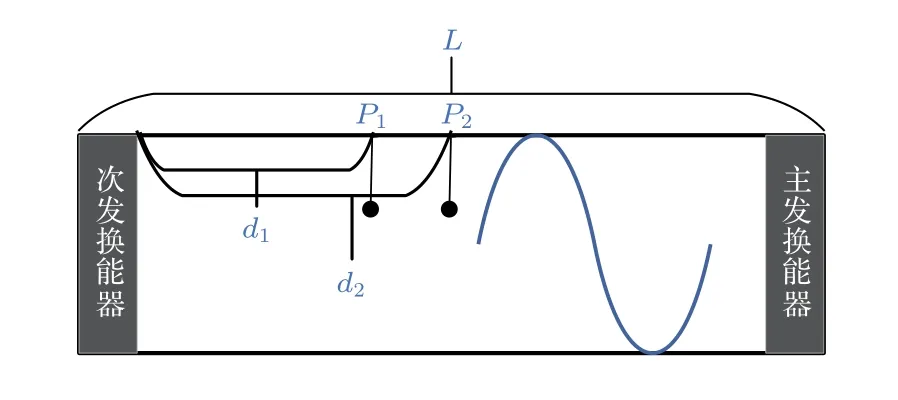
图2 行波管仿真模型Fig.2 Traveling wave tube simulation model

图3 为主发换能器发射1.5 kHz 的CW 正弦脉冲信号，此时次发换能器未发射抵消信号，声信号由次发换能器界面反射。通过双水听器法解算得到的次发换能器反射界面处的入射信号与反射信号。图4(a)为未考虑时延与幅度影响，次发换能器直接使用τ理论抵消反射波从而进行行波场建立的结果。可见由于换能器与外围电路的频响影响导致的时延偏移以及幅值偏移使得行波场建立失败。使用一维黄金分割搜索算法对时延与幅值进行搜索，行波场建立结果如图4(b)所示，搜索过程中的次发表面反射系数如图5 所示。可见使用黄金分割搜索算法成功地搜索得到正确的时延与幅值，从而完成了行波场的建立。

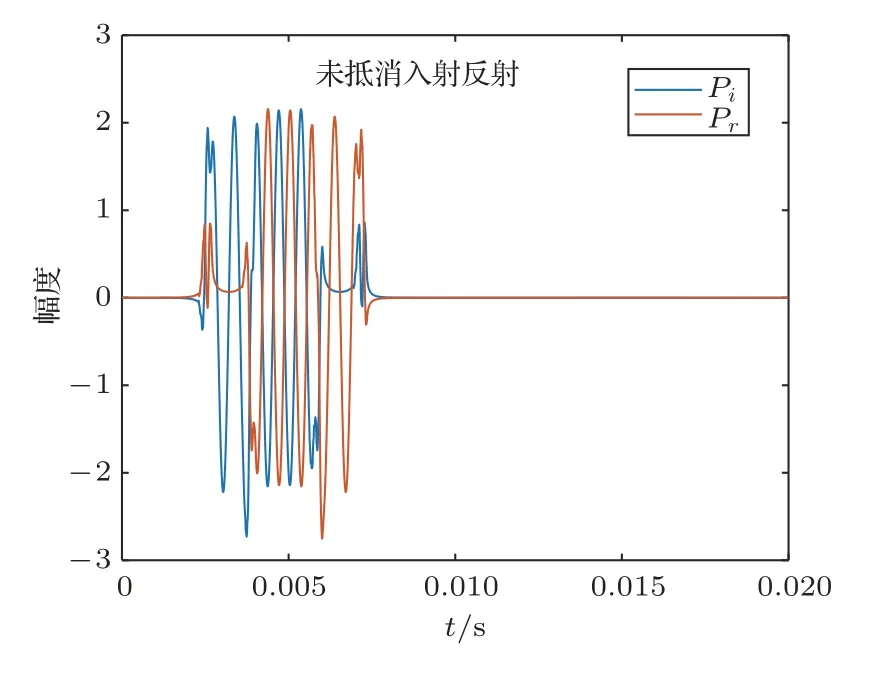
图3 1.5 kHz 时主发信号时域波形Fig.3 Time domain waveform of main signal at 1.5 kHz

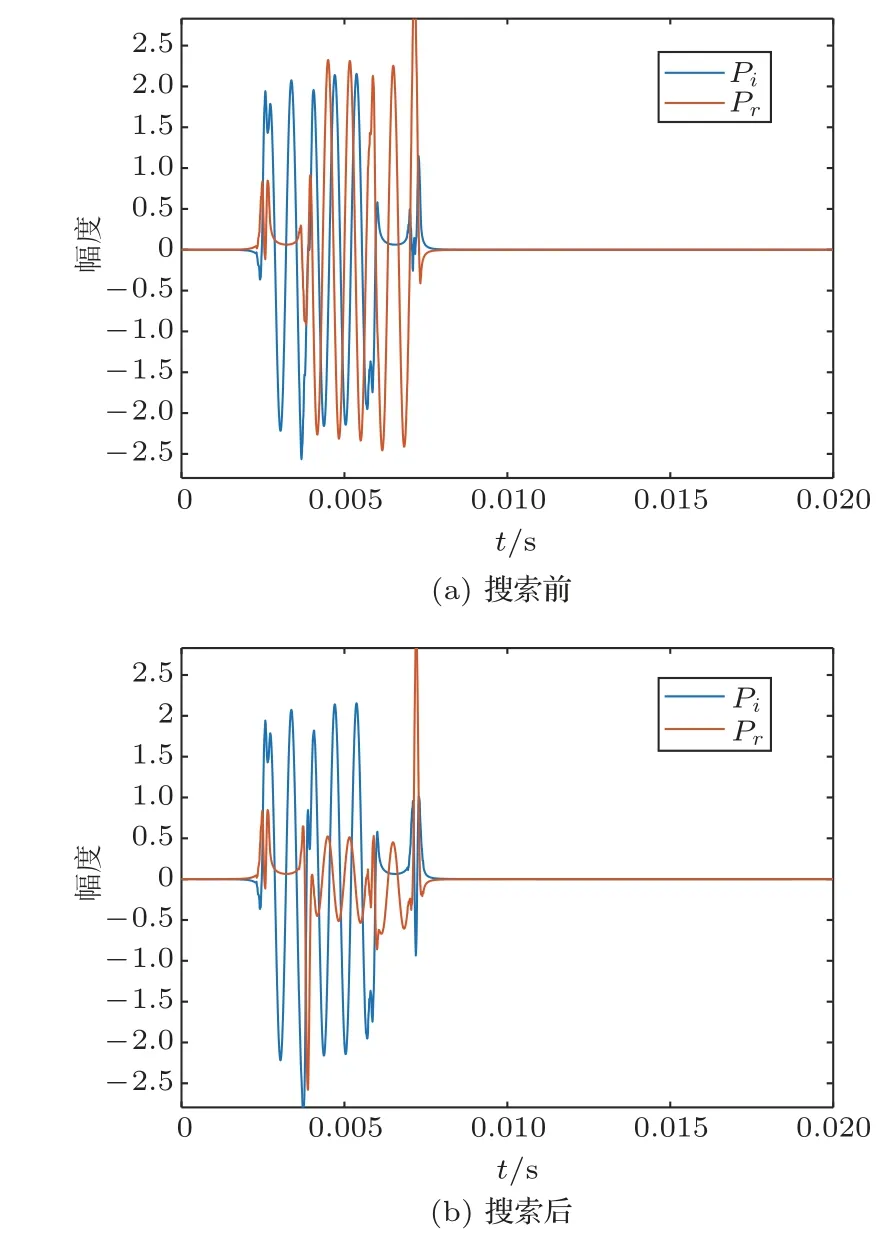
图4 搜索前后行波场建立结果Fig.4 Establishment of traveling wave field before and after search

图5 反射系数搜索曲线Fig.5 Reflection coefficient search curve

3 试验验证

为了验证算法和系统性能，作者在中国船舶工业系统工程研究院的行波管系统中进行了试验，使用LabView 编写了试验系统。该试验系统如图6所示。

以水柱为对象，使用本文算法在1.5 kHz 频率下进行时延与幅值搜索，以验证使用黄金分割算法建立行波场的效果。首先在固定幅值时进行时延搜索，得到最佳时延，并使用该时延进行幅值搜索，得到最佳幅值。1.5 kHz 频率下搜索时延与幅值时次发换能器处反射系数r随搜索次数变化的情况如图7 所示，其中横轴表示搜索次数，纵轴表示次发换能器处反射系数r。在给定初始幅值的情况下，以τ理论的正负半周期范围内进行最佳时延的搜索，随着搜索的进行，不断缩小搜索区间，当搜索区间宽度小于门限值后，时延搜索停止，得到最佳时延。然后使用得到的最佳时延，在允许输出范围内进行幅值搜索，以得到最佳幅值。可见在搜索时延的情况下，次发表面的反射系数r迅速下降，而搜索幅值的情况下反射系数r下降缓慢，说明此时行波场建立已经趋于收敛。当搜索结束后，次发反射系数r约等于0.05，可以认为此时行波场已经建立。

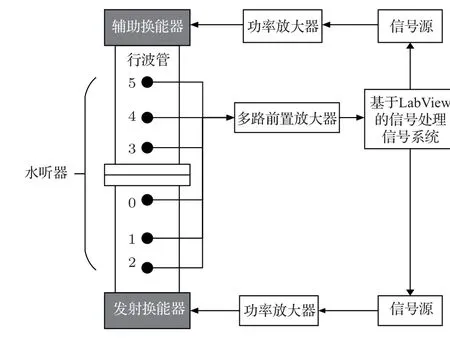
图6 行波管测量系统框图Fig.6 Traveling wave tube measurement system block diagram

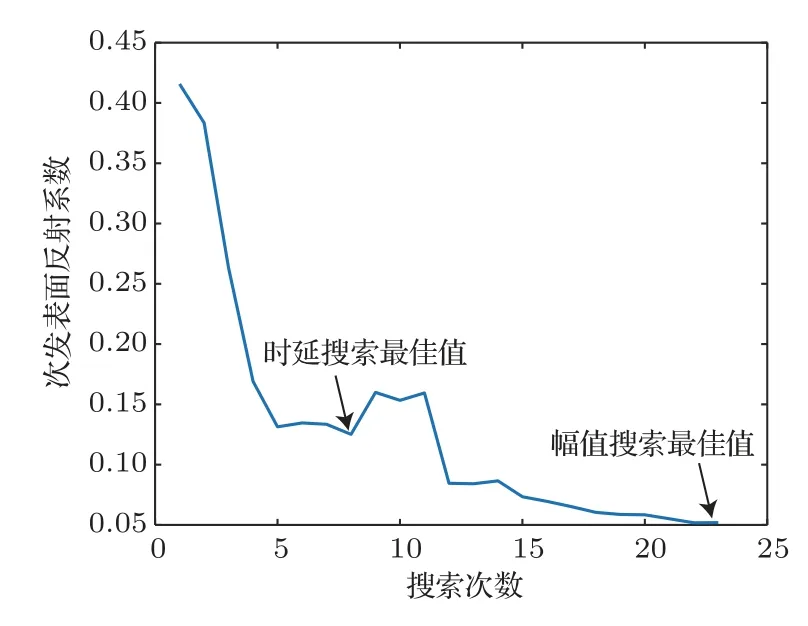
图7 1.5 kHz 下次发表面反射系数搜索结果Fig.7 Search result of interface reflection coefficient of secondary transducer at 1.5 kHz

对水柱进行1 kHz∼3 kHz 范围内以100 Hz 为间隔的声学参数测量，结果如图8所示，其中横轴表示频率点，纵轴表示无量纲系数。可见透射系数与水柱的理论值符合较好，但是反射系数测量误差较大，其原因可能与双水听器法误差有关，产生双水听器法误差的原因包括传递函数的测量误差与反射、透射系数的计算误差与声速测量误差[6]。

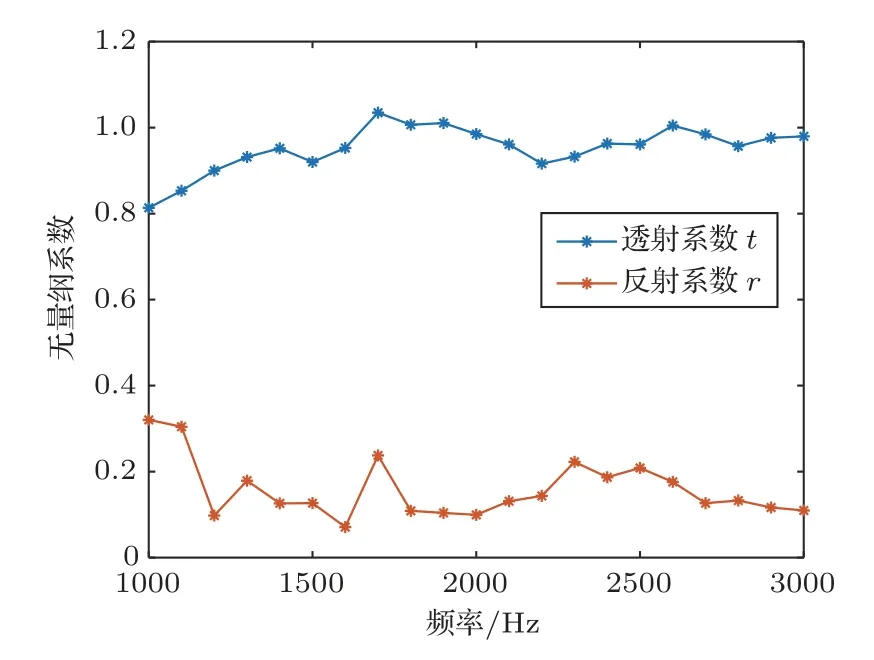
图8 水柱声学参数测量结果Fig.8 Measurement result of acoustic parameters of water cylinder

对30 mm 厚度的钢板进行1 kHz∼3 kHz 范围内以100 Hz为间隔的声学参数测量，并与理论值进行对比，结果如图9 所示，其中横轴表示频率点，纵轴表示无量纲系数。可见，透射系数t测量结果与理论值符合得较好，说明本系统测量透射系数较为准确，但是反射系数r比理论值偏小，且曲线不光滑，测量反射系数误差较大。将t与r的测量值与理论值的相对误差做柱状图如图10 所示，其中横轴表示频率点，纵轴表示无量纲相对误差。可见，除了少数频点，透射系数的相对误差都低于10%，但是反射系数的误差较大。反射系数误差较大、透射系数测量误差较小，这与水柱声学参数测量结果趋势一致。

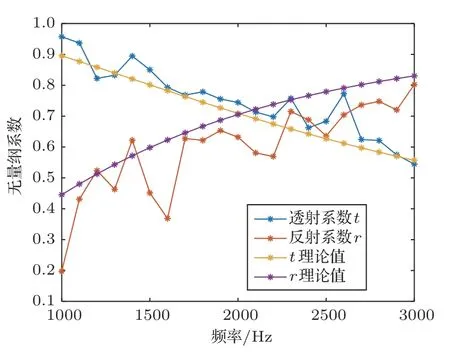
图9 30 mm 钢板声学参数理论值与测量值对比Fig.9 Comparison between theoretical and measured acoustic parameters of 30 mm steel plate

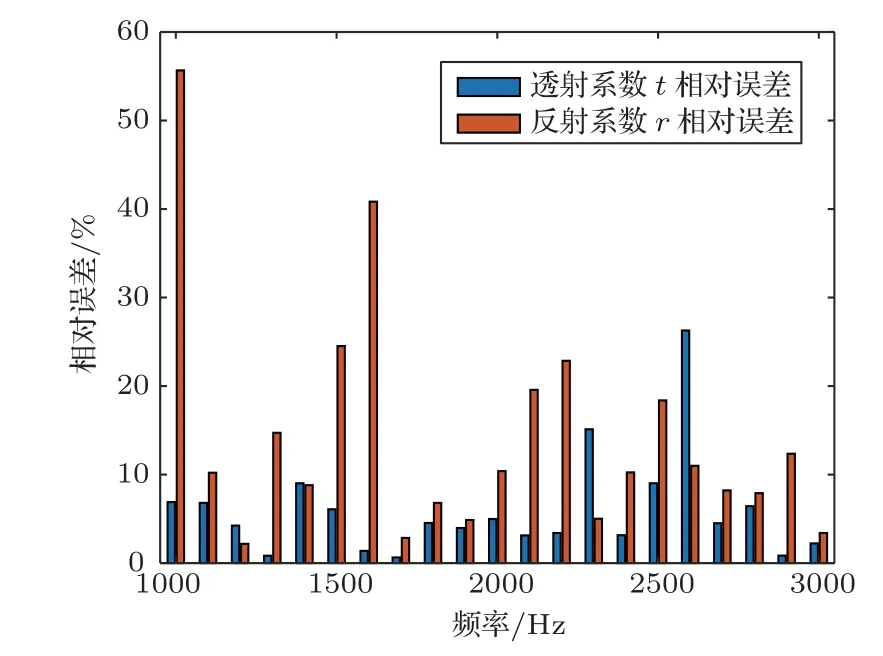
图10 30 mm 钢板测量相对误差Fig.10 Measurement relative error of 30 mm steel plate

4 结论

本文通过一维黄金分割搜索算法，对幅度A与时延τ时延进行搜索，实现CW 脉冲信号的行波场建立。该方法能够快速建立行波场，从而实现声学参数测量，但是该方法并不能对发射波形进行精细的修改，从而更加匹配建立最佳行波场所需的最佳幅度谱M与相位谱φ，进一步的工作可以考虑对发射波形进行均衡，从而提高行波场建立效果。本文使用该算法进行了行波场建立，并使用测量系统对水柱以及钢板的声学参数进行了测量，验证了该系统的可行性。具体如下：

(1)使用黄金分割算法能够得到抵消反射波所需的时延与幅值，实现有源吸声，完成行波场的建立。

(2)对钢板和水柱的测量结果表明，本系统声学参数测量与理论值符合较好。