基于L-曲线参数优化的均匀声场重建算法

张 旭 赵洪亮 程希光 裴景春

(1 山东科技大学电子信息工程学院 青岛 266590)

(2 山东科技大学电气与自动化工程学院 青岛 266590)

0 引言

扬声器阵列的均匀声场重建是指控制扬声器阵列输入的幅值和相位，使得控制区域的重建声场均匀化，同时增大明区能量占比。为达到目的，已提出多种控制方法，大体可分为两类：一类将建立能量控制作为目标函数，如能量对比度控制(Acoustic contrast control,ACC)法[1−2]、声能量差最大化控制(Acoustic energy difference maximization,AEDM)法[3]等；另一类将声场重建误差作为目标函数，如基于最小二乘准则的多点匹配法(Pressure matching with the least-squares criterion,PM-LS)[4−5]等。

在声场重建中，往往出现不适定问题[6]。其中最常用的是使用Tikhonov 正则化来解决不适定的声场问题[7]，而正则化程度取决于正则化参数。对于正则化参数的选取，文献[8–9]中提出了使用平滑矩阵的广义Tikhonov 正则化。在文献[8]中，导数平滑范数应用于自适应波场合成，以减少扬声器激励信号的相位变化。Betlehem 等[2]设计了一种方法，计算扬声器权重的平方和来限定Tikhonov参数上限，然后采用牛顿法确定正则化参数。另一个方法就是截断奇异值分解(Truncate singular value decomposition,TSVD)，对传递矩阵进行奇异值分解，并且只有较重要的特征值才会被用于声场重建。该方法减少并消除了较小奇异值对解的影响，但是对于正则化参数的选取很难确定一个合理的标准[10]。同时扬声器阵列功率受到物理系统的制约，需要考虑扬声器驱动信号功率与重现误差之间的平衡问题。因此怎样在考虑扬声器功率限制的同时合理地选择正则化参数是亟需解决的问题。

在本文中，声场重建模型以最小化声场重建误差为目标函数，并约束扬声器功率上限。针对正则化参数选择问题，将L-曲线法[11]引入均匀声场重建，该方法以重建误差作为横轴，扬声器功率作为纵轴得到拟合曲线，然后选取该曲线上曲率最大的点所对应的参数值作为Tikhonov 正则化参数的选值。作为对比，分别用传统最小二乘法、广义交叉验证(Generalized cross-validation,GCV)法以及L-曲线法进行性能仿真，并在限定功率下对明区重建声场进行测试。仿真及实验证明，L-曲线法平衡了扬声器功率与重建误差，且阵列能量效率较高，具有良好的声场重建效果。

1 基于L-曲线法的均匀声场重建算法

1.1 均匀声场重建模型

将控制区域划分为明区以及暗区。明区为目标声场，为达到良好的均匀声场，该期望声压幅值设为1。基于最大化控制目标区域声场能量的目的，设置暗区并将暗区期望声压设为0。声场重建区域明暗区划分如图1所示。

图1 声场重建区域明暗区示意图Fig.1 Schematic diagram of the light and dark area of the sound field reconstruction

在控制区域0∼B3内，明区范围B1∼B2设置M个控制点，暗区0∼B1以及B2∼B3设置N个控制点。明暗区通过控制点到阵元的距离(m=1,2,··· ,Mb)和(m=1,2,··· ,Nd)得到相应的阵列响应和而对于L个扬声器阵元权重gL，两者关系表示如下：

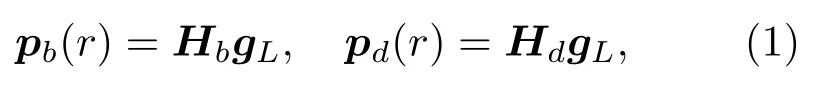
式(1)中，Hb为明区传递矩阵，Hd为暗区传递矩阵。传递矩阵可定义为

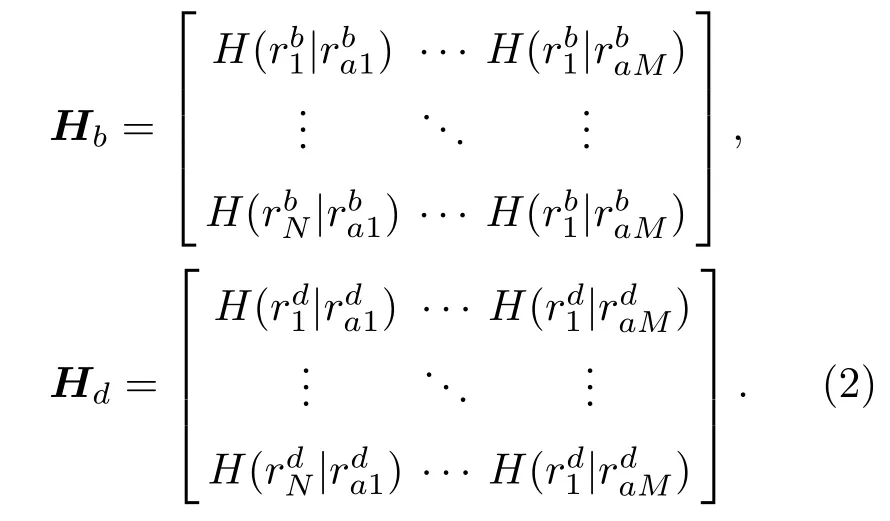
整个控制区的传递矩阵Hc=[Hb,Hd]T，控制区期望声压Pc=[Pb,Pd]T。

本文优化模型是在考虑最小化控制区域重建声场的误差函数的基础上，约束扬声器权重的平方和上限，其优化模型如下：

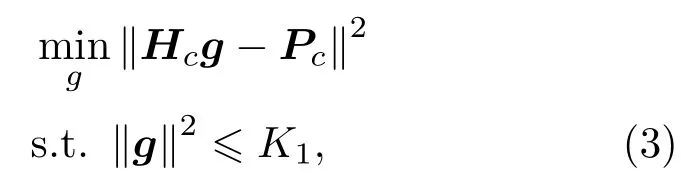
其中，∥·∥为2-范数，g为扬声器权向量，K1为其扬声器功率限制参数。

1.2 L-曲线选取正则化参数

为获得扬声器阵列权重，需对优化模型进行求解。式(3)具有二次目标和单个二次约束，因此该优化模型为凸优化问题。式(3)对应的广义拉格朗日罚函数可以写为

式(4)中，λ为扬声器阵列约束权重因子，用于平衡重建声场误差与扬声器权重g，λ0。式(4)可通过求解，得到扬声器权向量如下：

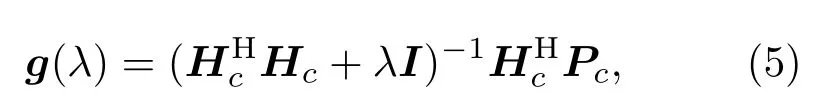
式(5)中，H 为共轭转置，I为单位矩阵。矩阵Hc不是满秩矩阵，因此进行奇异值分解(Singular value decomposition,SVD)，如下：

其中，Σ ∈Rn×n为对角矩阵，Σ=diag(s1···sn),s1s2···sn0。U ∈Rm×n和V ∈Rn×n分别为m×n和n×n阶酉矩阵：

因此，式(5)可以改写为

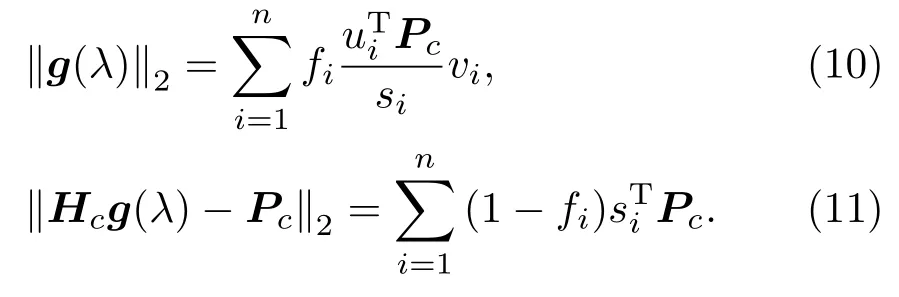
以µ=lg∥Hcg(λ)−Pc∥2为横轴、v=lg∥g(λ)∥2为纵轴并以λ为参量得到拟合曲线，该曲线上曲率最大的点所对应的参数，就是L-曲线法选择的正则化参数λL，该曲率最大的位置即为L-Corner，其表达式为

其中，µ′、v′和µ′′、v′′分别是µ、v对λ的一阶、二阶导数。将求得的参数值λL带入式(5)得到扬声器阵列权向量gL。

1.3 声场均匀控制的性能指标

为衡量扬声器阵列在控制区域的均匀声场重建效果，本文从以下三个参数对重建声场性能进行评价，分别为明区重建均方误差、阵列能量效率以及声场均匀度。重建性能指标如下。

1.3.1 明区重建均方误差

定义为明区重建声场与期望声场的声压幅值之差的均方和与期望声场的声压幅值均方和之比，如式(13)所示：

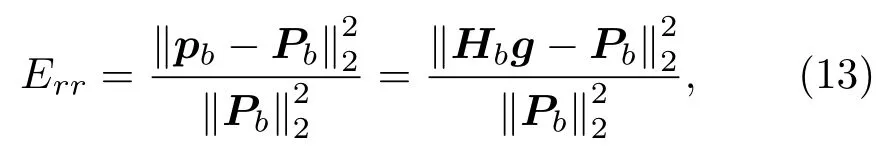
式(13)中，pb、Pb分别为明区重建声场声压与明区期望声压；Hb为明区传递函数矩阵。该指标用于衡量声场重建效果的准确度。

1.3.2 声能量阵列效率

除了明区重建误差外，仿真中还需要比较各种情况下扬声器阵列辐射到目标区域的声能量大小，本文使用扬声器阵列在明区的声能量效率进行评价，明区控制点上平均声能量可以表示为

式(14)中，Q为目标区域控制点的数量，ptm为明区中第m个控制点的阵列响应，Hb为对应的扬声器阵列单元到明区内控制点的传递函数矩阵。阵列能量效率的定义为明区M个控制点的平均声能量与扬声器阵列输出总能量的平均声能量的比值，其表达式如下：

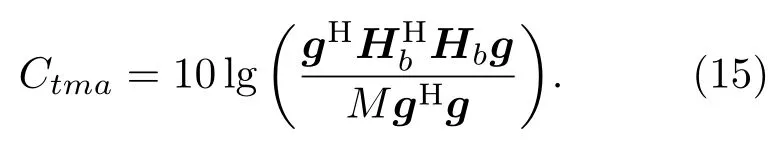
该方程代表了扬声器阵列辐射到明区的声能量效率，即对总能量的利用效率。方程中对控制区域控制点的能量取均值是为了避免控制点数量的变化对该参数的影响。

1.3.3 明区声压级均匀长度和声压级波动标准差

对声场均匀度进行评价时，主要采用明区的均匀长度和声压级波动的标准差两个参数。明区的均匀长度定义为明区声压幅值与均值相差少于变动范围3 dB 内的距离长度，该指标可以反映出明区中均匀声场所占的比例。而明区声压级波动的标准差则可以反映出重建区域整体的声场波动情况。明区的均匀长度rT和声压级波动的标准差Sd分别表示为

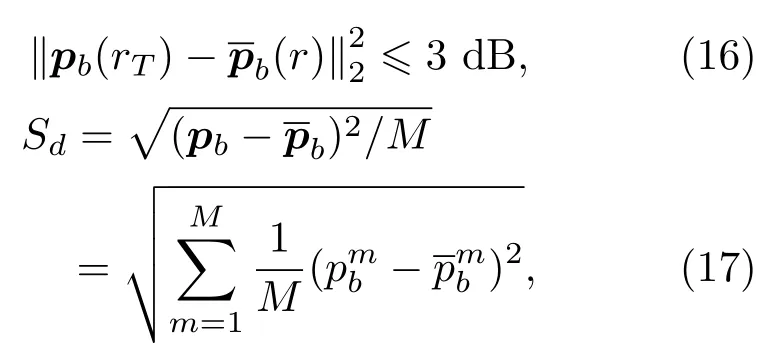
其中，表示为明区声压向量的均值；pb(rT)为符合条件的明区声压向量；M为明区的控制点数量。

2 数值仿真

2.1 L-曲线法的参数仿真

如图1 所示，取扬声器阵元个数L=16，激励频率f=1000 Hz，阵元间距d=0.1 m，阵列高度H1=7 m。在控制区0∼60 m 内，设置10∼50 m为明区范围，即保持声场均匀的区域，其余为暗区范围。控制区期望声场Pc=[Pb,Pd]H。Pb、Pd分别为明区期望声压和暗区期望声压。基于暗区声压数值尽量小的考虑，因此设置Pd=[0,0,··· ,0N]H。明区期望声压表示如下：

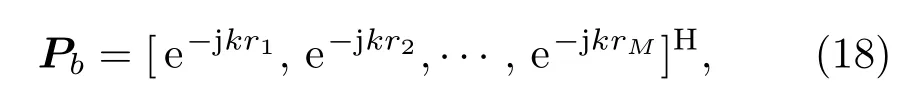
其中，r=[r1,r2,...,rM]为阵元中心到明区控制点的距离。对重建模型根据L-曲线法求解λ拟合图，如图2所示。

由图2 可以看出f=1000 Hz 时，拟合曲线有一个非常明显的拐角(L-Corner)，该拐角位于L-曲线的垂直部分与水平部分相交的位置。水平分布所对应的正则化解主要由明区重建误差主导，而垂直部分由扬声器权重主导。因此，L-曲线的这个拐角为扬声器权重与明区重建误差都较小的一个平衡点。因而在拐角处得到参数值，即λL=0.37874。相应地，在阵列频率为0∼4000 Hz 时，λL对应的取值如图3所示。可以看出，λL在低频段取值在0.4左右，在频率为3500 Hz 以上的高频段最优取值为1左右。

图2 L-曲率拟合图Fig.2 L-curvature fit map

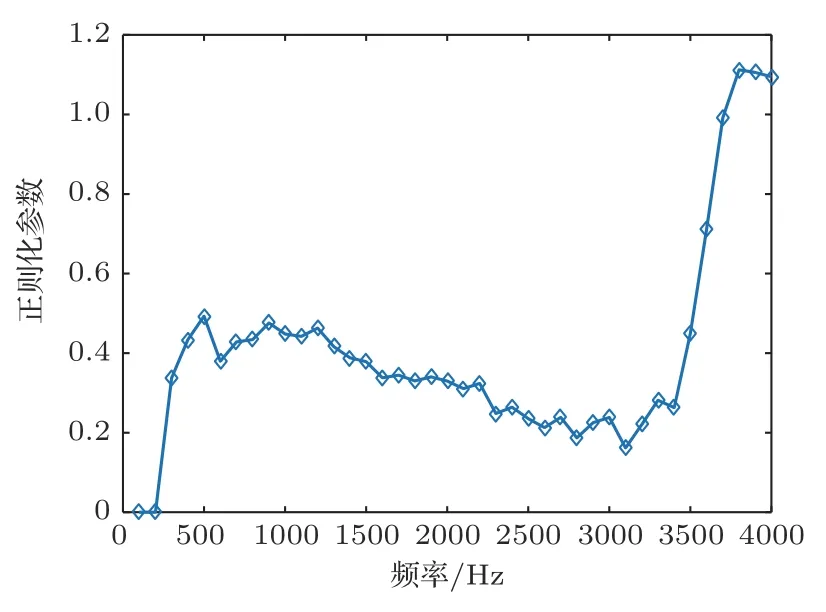
图3 λL 取值Fig.3 λLValue

2.2 重建性能指标仿真

激励频率范围设置为0∼2000 Hz，为有效重现该范围内的声场，选取阵元间距为d=0.1 m。根据定义的性能指标，在0∼2000 Hz 频带上，分别对传统最小二乘法、GCV 法以及L-曲线法进行仿真比较。

如图4(a)、图4(b)所示，可以明显看出在低频段约0∼600 Hz，未正则化的最小二乘法声场重建均匀度存在明显的波动，而高频段声场均匀度随着频率的变化较为连续且对应的曲线较为平滑。阵列能量效率在0∼600 Hz 频段内较低，波动范围为−160∼−140 dB，而在600∼1400 Hz 间，阵列效率频率上升而提升至−20 dB。基于以上分析可以看出，传统的最小二乘法存在低频段能量过低以及均匀度波动问题。

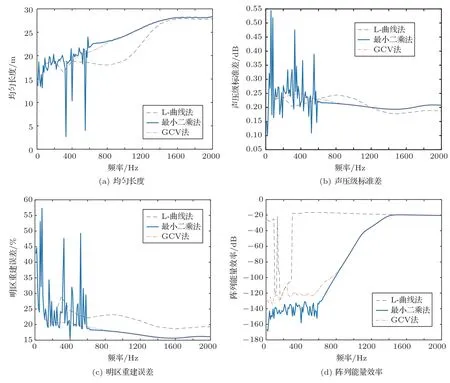
图4 重建性能指标仿真对比结果Fig.4 Reconstruction performance index simulation comparison result

为了改善该情况，需要对其进行正则化处理。对于正则化因子的选择，仿真选取了GCV 法与L-曲线法进行对比。GCV 法选择最佳正则化参数就是选取使GCV 函数Gλ最小时对应的λ值。从图4中可以看出，基于GCV 法选择的正则化参数平滑了低频段的波动，均匀度稳定且随着频率增加而上升，重建误差在20%以下。然而图4(d)显示GCV法由于追求重建误差，阵列能量效率没有显著提升。

GCV 法与L-曲线法皆可以对传统的最小二乘法低频段波动进行优化，相比于GCV 法，L-曲线法的阵列能量效率整体提升了130 dB,极大改善了低频段的阵列能量效率过低的问题。均匀长度方面如图4(a)、图4(b)所示，L-曲线法在0∼1000 Hz 频段与1400∼2000 Hz 频段分别保持一致，并且整个频段声压级标准差变化平缓，波动在0.2∼0.25 之间。基于L-曲线法的明区重建误差在25%，整体均匀只在频率300 Hz处有一个波动。图4(c)结果表示基于L-曲线法的重建误差低于GCV 法的重建误差5%，该原因是L-曲线法约束了扬声器功率，牺牲了一定程度的重建误差。GCV 法为了到达良好的重建误差，增加了扬声器阵列输出，因此GCV 法阵列能量效率较低。在实际系统实现中，扬声器功率是极为重要的指标，因此L-曲线法平衡了扬声器功率与重建误差，更为符合实际要求。

3 实验比较

本节将扬声器阵列未控制的声场效果与GCV法及L-曲线法的重建声场进行比较。本实验将明区声场缩小为1∼5 m，阵元中心距离地面为2 m，扬声器阵列数量为16个，阵元间距为0.6 m，测量间距为0.2 m，如图5所示。期望声压设为85 dB，并将三种方法的扬声器功率均设置为以L-曲线功率为标准进行计算。实验以及仿真频率均取1000 Hz，在此频率下，L-曲线法取正则化参数值为λL=0.4480，GCV法取参数值为λG=2.66×10−5。

图5 实验装置图Fig.5 Experimental setup diagram

首先对L-曲线法及GCV 法进行均匀声场重建仿真。如图6所示，该声场左侧声压最大值处为扬声器阵列，阵列根据求得的扬声器权重偏转一定角度，在明区范围内进行均匀声场重建。由图6 的声压级分布图可以看出，L-曲线法在明区重建区域误差以及均匀度略差于GCV 法。然而，GCV 法的阵列处声压级明显高于L-曲线法。该结果说明若在明区达到相同的期望声压级，GCV法中扬声器阵列需要更高的功率，与性能仿真分析结果一致。

实验时，使用FPGA 系统产生信号经功率放大后驱动16独立通道扬声器阵列，信号测量采用声传科技公司的CHZ-215型传声器头和YG-201型前置放大器组成的宽带测量传声器。测量结果如图7(b)所示，与仿真结果(图7(a))基本一致。在这三种方法中，未控制的声场整体声压级最小，且均匀度较差，地面位置2.5 m处甚至出现较明显的谷点。基于GCV 的正则化参数法均匀度要优于L-曲线法，该声压级波动范围为8 dB。但是因为实际实验中扬声器功率限定，该平均声压级低于期望声压85 dB。L-曲线法的重建声压级整体高于GCV 法5 dB，且在期望声压级上下波动，波动范围为10 dB。

为确保算法的正确性，实验分别采集频率为500 Hz、1500 Hz 和2000 Hz 时的声压数据并与1000 Hz 进行对比，如图8 所示。可以看出相同功率下，在0∼1000 Hz 范围内L-曲线法整体声压级高于GCV 法5 dB 以上，并且高频段L-曲线法均匀度以及重建误差与GCV 法持平。另一方面L-曲线法在不同频率下重建声压值皆在85∼90 dB 范围内，而GCV法波动较大。因此L-曲线法在实际应用中更具有优越性。该实验证明，基于L-曲线法的最小二乘法声场重建算法在功率限定的条件下，阵列能量效率较高，更符合实际需求，与性能仿真结论一致。

图6 L-曲线法和GCV 法均匀声场重建仿真Fig.6 Simulation of uniform sound field reconstruction using L-curve method and GCV method

图7 三种方法的明区声压级分布Fig.7 Sound pressure level distribution in bright area of three methods

图8 不同采集频率下声场测试结果Fig.8 Sound field test results at different acquisition frequencies

4 结论

针对声场重建模型正则化参数选取的问题，本文将L-曲线参数选择法引入声场重建算法，并对比了GCV 与L-曲线法声场重建性能。相对于GCV法，L-曲线法更具有优势，计算L-Corner 是一个容易定义的数值问题，并且该方法很少受到相关性误差的影响。本文以均匀度、明区能量占比以及明区重建误差作为评价标准，对L-曲线法与GCV 法以及最小二乘法进行仿真以及实验比较。仿真以及实验结果显示，L-曲线法实现了重建误差与扬声器驱动信号功率之间的平衡，克服了低频段不稳定的问题，其缺点是低频段均匀度要差于GCV法。