基于几何级数展开的鬼波压制方法∗

陈宝书 吴 玉 陶 杰 管西竹 刘春城 符力耘

(1 中海油研究总院有限责任公司 北京 100028)

(2 中国科学院油气资源研究重点实验室 中国科学院地质与地球物理研究所 北京 100029)

(3 中国石油大学(华东)地球科学与技术学院 青岛 266580)

0 引言

随着海上油气勘探开发难度的增加，地质、地球物理学家对地震资料的品质要求越来越高。常规的地震资料处理流程已经不能满足日益增长的对地震资料品质的要求。地震资料的频带宽度和地震资料的分辨率直接相关，高分辨率的地震数据对后续的构造精确解释、储层准确描述具有重要影响。因此，宽频处理技术是当前地震处理流程非常重要的一环。对于海上拖缆数据，因为海平面是一个强反射界面(反射系数接近−1)，上行的反射波(一次波)在海平面发生向下反射(鬼波)，上行波和下行鬼波叠加在一起，降低了地震资料的分辨率。为了恢复宽频的上行波，需要把下行鬼波的干涉去掉，这项技术被称为鬼波压制。

近些年来，发展了很多鬼波压制的技术和方法，主要可以分为两大类：(1)与采集技术相关，通过特定的观测系统设计达到有效压制鬼波的目的，主要包括上下缆[1]、变深度缆[2−4]、双检波器[5]；(2)基于处理技术的方法，基于镜像道集和联合反褶积的鬼波压制方法[2]、基于自举法确定鬼波参数的方法[6−7]、基于波动方程的鬼波压制方法[8−9]。

在Radon 域通过求解一个最小二乘问题可以消除虚反射产生的鬼波[10]。对含鬼波的地震数据进行两次波场外推延拓，对延拓结果进行求和及阈值截断处理，可以达到去除鬼波的目的[11]。通过波动方程延拓，把鬼波压制看作一个反演问题，通过反问题的求解可以得到只包含上行波的地震记录[12]。基于格林函数理论的鬼波压制方法完全基于地震数据驱动，无需任何地下介质信息，适用于各种复杂的海洋地形和地质情况[13−14]。针对上下缆数据，可以通过上下缆地震波场的波动方程法合并有效解耦鬼波干涉，实现综合利用上下缆地震数据压制鬼波[15]。

目前这些鬼波技术还存在一些问题和限制，基于特定观测系统的鬼波技术通常在平缆数据上不能得到很好的结果，但是目前常规采集的拖缆数据很大一部分是平缆采集，这部分资料的潜力还有待挖掘。基于处理技术的鬼波压制方案，因为鬼波算子在陷波频率附近接近于0 (上行波和下行波刚好抵消)，直接对算子求逆，存在数值不稳定的问题，即使采取一些技术手段来规避这个问题，如基于波动方程的鬼波压制技术[8]因为在时空域进行鬼波压制，可有效解决稳定性问题，但是在时空域求解波动方程通常计算量比较大。为了同时解决稳定性和计算效率的问题，本文提出一种在频率波数(FK)域进行波动方程延拓压制鬼波的技术。该技术首先对逆鬼波算子进行几何级数展开，解决逆鬼波算子的稳定性问题，然后在FK 域进行波动方程延拓，解决计算效率的问题。

1 方法原理

1.1 鬼波算子

简单而不失一般性，假设如图1 所示的简单模型，下行的入射波场从震源出发，在海底发生反射向上传播被检波器接收(一次波：蓝线)，因为海平面的存在，上行的反射波(一次波)被海平面反射后(下行波)被检波器接收(鬼波：红线)，因为鬼波的干涉作用，导致接收的波场存在陷波效应：某些频率的能量为0，这是由一次波和鬼波刚好反相叠加导致的。

图1 一次波和鬼波的传播路径Fig.1 Raypath of primary and ghost wavefield

假设海平面的反射系数等于−1，缆深为zr，在FK域鬼波算子可以表示为[16]

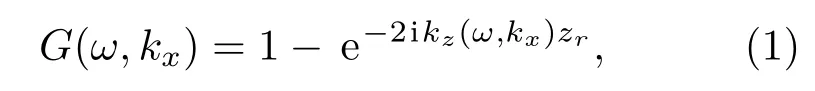
鬼波算子是一个二维时空域TX 褶积算子(三维对应TXY 域褶积)[17]，因此其逆算子(反褶积算子)可以在TX 域进行，也可以在FK 域进行。因为可以借助快速傅里叶变换(FFT)进行快速计算，因此FK域方法在计算效率上有优势。

图2 鬼波算子在FK 域和在TX 域的响应Fig.2 Ghost operator in FK domain and TX domain

1.2 基于几何级数展开的逆鬼波算子

1.2.1 常规FK域鬼波压制算子

满足模型假设的前提下，如果准确知道缆深数据，逆鬼波算子可以表示为[17]

公式(2)在陷波频率下存在奇异性(G算子在陷波频率处等于0，见图2)，直接求逆存在数值不稳定问题。为了解决这个问题，可以把鬼波压制问题看作一个最小二乘反演问题：

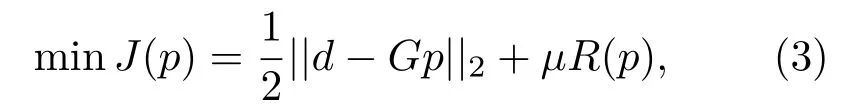
其中，p表示一次波数据，d表示含鬼波的地震数据，R是正则化算子，目的是对一次波数据进行某种约束，使得公式(3)具有唯一解，µ是正则化参数。通常R算子取为p的二范数，这时公式(3)对应的形式解为

其中，I表示单位算子。公式(4)可以得到一个稳定的鬼波压制结果，但是在陷波频率处的能量并没有补偿，这个不难理解：在陷波点，地震数据d的能量等于0，在不引入先验信息的情况下，不可能恢复已经丢失的信息。下面通过一个简单的数值算例说明这一点。设计一个简单的一维算例，缆深等于25 m，合成的含鬼波记录及其频谱见图3(a)，从频谱上可以看到陷波效应，因为鬼波的存在，导致地震信号的有效频带变窄，图3(b)是根据公式(4)压制鬼波以后的结果，可以从频谱上看出，陷波频率处的信号能量没有得到补偿，导致波形出现了扰动。为了解决这个问题，回到逆鬼波算子式(2)，对其进行几何级数展开。

图3 一维鬼波压制算例Fig.3 1D deghosting example

1.2.2 基于几何级数展开的逆鬼波算子

针对逆鬼波算子式(2)，可以对其进行几何级数展开[17]：

公式(5)目前还没有消除奇异性，因为需要对无穷多项求和。为了解决这个问题，需要对公式(5)进行分析，明确每一项的含义。第一项是单位算子，第二项表示一个波场延拓算子。

以图3 为例，前两项和前三项之和见图4，从图4 可以看出，随着式(5)每一项的加入，鬼波和一次波分得越来越开，当加到无穷多项时，一次波和鬼波距离无限远，通过截取序列前面部分数据，把鬼波丢掉，可以得到只含一次波的数据。

图4 一维算例(图3)公式(5)前两项和与前三项和Fig.4 1D deghosting example of Equation (5):sum of two terms and three terms

一个简单的方法：对地震数据在时间方向进行补0，d(t)从nt长度变为2×nt长度，截取公式(5)有限项进行叠加，对得到的结果只取前nt个采样点，可以得到压制鬼波的记录p(t)。对于图3的一维算例，采用公式(5)进行鬼波压制，结果见图5。从频谱上可以看出陷波频率处的能量得到了很好的补偿，公式(5)通过波场延拓的方式不断地预测鬼波，然后把鬼波从记录中减掉，这样可以完全恢复一次波的信号。

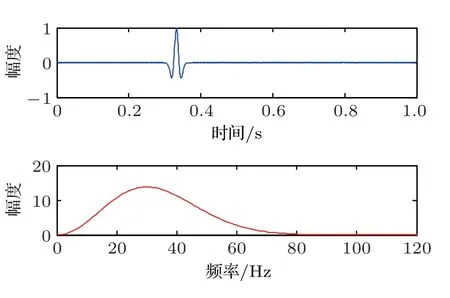
图5 一维算例公式(5)压制鬼波结果Fig.5 1D deghosting example of Equation (5):final outcome

2 数值算例

为了进一步验证本文方法的正确性，首先设计了一个简单的层状介质模型(图6)，网格间距为6.25 m×6.25 m，震源子波是主频50 Hz 的高斯子波，缆深25 m，缆长4000 m，最小偏移距200 m，震源位置(x,z)为(50 m,6.25 m)，时间采样步长0.25 ms，记录长度3.5 s。

图7(a)是不含鬼波的理想数据，是鬼波压制的目标；图7(b)是含鬼波数据，从其FK 谱上可以看到明显的陷波效应(图中黑色箭头所示)。压制鬼波算法的目的是对陷波频率处的波场能量进行有效恢复。

首先对图7(b)的数据利用公式(5)进行鬼波压制处理，得到的结果见图8。通过与理想的不含鬼波记录的相比较，肉眼几乎看不出差别，这个简单算例表明算法的有效性。

为了验证算法对复杂模型的适用性，本文设计了一个复杂的起伏海底模型(图9)，网格间距为6.25 m×6.25 m，震源子波是主频50 Hz 的高斯子波，缆深25 m，缆长2500 m，最小偏移距200 m，震源位置(x,z)为(50 m,6.25 m)，时间采样步长0.25 ms，记录长度3.5 s。

图10(a)是不含鬼波的理想数据；图10(b)是含鬼波数据，从其FK 谱上可以看到明显的陷波效应。为了测试本文方法对复杂模型的适用性，对图10(b)的数据利用公式(5)进行鬼波压制处理，得到的结果见图11。通过与不含鬼波记录的图10(a)比较，可以看出本文方法压制鬼波的有效性。

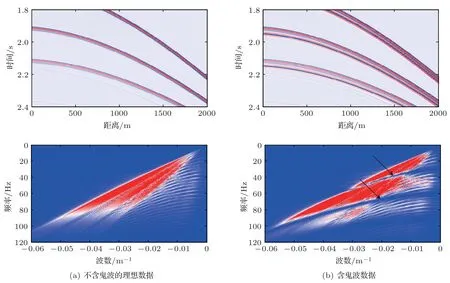
图7 不含鬼波的理想数据和含鬼波数据及其FK 谱Fig.7 Seismic data without and with ghost

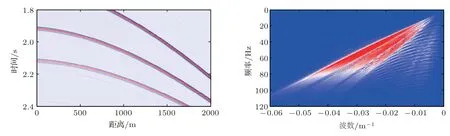
图8 图7(b)数据利用公式(5)压制鬼波以后结果Fig.8 Deghosting outcome of Equation (5)for seismic data with ghost

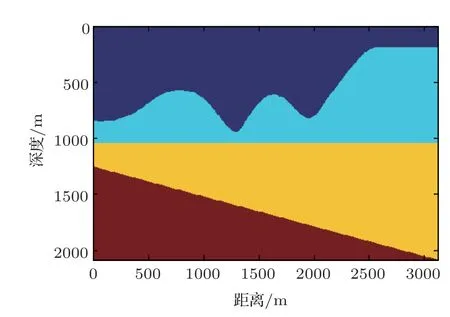
图9 起伏海底模型Fig.9 Velocity model of fluctuating seabed

为了验证本文方法在实际资料上的效果，选取了某海上实际拖缆数据，拖缆长度为6 km，共有480道检波器，检波器间隔12.5 m；时间采样间隔2 ms，采样点数6144；拖缆沉放深度20 m。图12(a)为实际采样的共炮点道集数据。对实际数据进行频谱分析，见图13(a)，可以看到明显的陷波效应。利用公式(5)对实际数据进行鬼波压制，结果见图12(b)，相比实际数据，鬼波明显被压制。从对图12(b)进行频谱分析，见图13(b)，可以看到陷波点能量得到了有效补偿。通过波形和频谱的对比，可以验证本文方法对实际数据的有效性。

图10 不含鬼波的理想数据和含鬼波数据及其FK 谱Fig.10 Seismic data without and with ghost

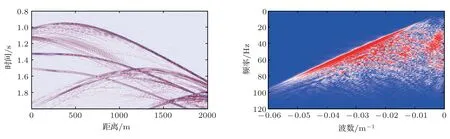
图11 鬼波压制结果及其FK 谱Fig.11 Deghosting outcome of Equation (5)for seismic data with ghost

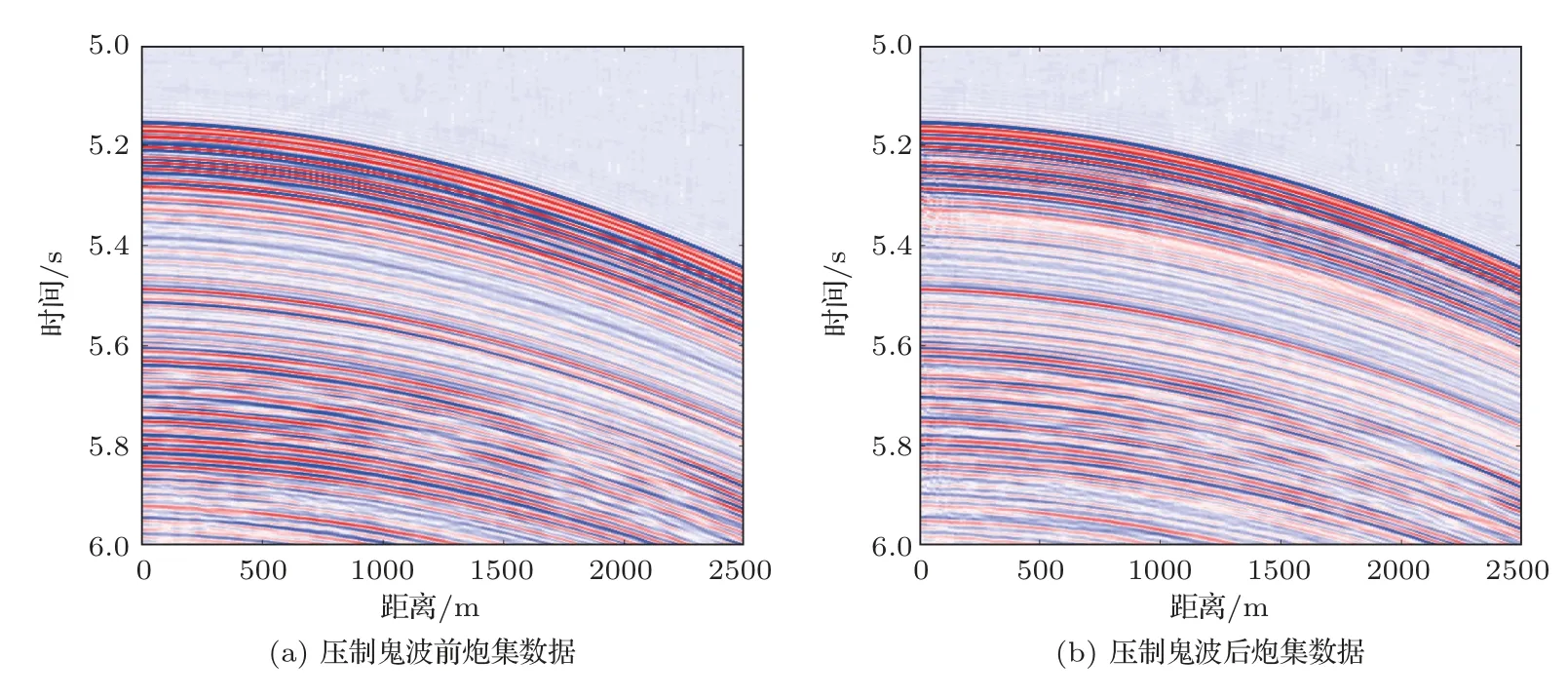
图12 实际资料及其压制鬼波以后结果Fig.12 Real seismic data and deghosting outcome

图13 实际资料及其压制鬼波以后结果：频谱Fig.13 Real seismic data and deghosting outcome:spectrum

3 结论

本文提出了一种基于逆鬼波算子几何级数展开的压制鬼波方法，该方法结合了波动方程压制鬼波算法和FK 波场延拓技术的优势：通过级数截断克服逆鬼波算子的奇异性问题，利用FFT实现波场的快速延拓。二者优势的结合使得该算法具有精度高、计算耗时短的特点，数值算例表明了本文方法的有效性。

与常规的基于反演的迭代类算法相比，本文方法不用确定正则化参数，只要知道缆深数据就可以计算，减少了参数调试的时间。