基于有限时间观测器的Buck变换器的快速终端滑模控制
丁方莉,周同旭
(1.铜陵学院 电气工程学院,安徽 铜陵 244061;2.皖西学院 机械与车辆工程学院,安徽 六安 237012)
Buck型变换器是一种结构简单的直流-直流降压变换器,其利用开关功率管的通和断,控制电流的导通和切断,同时在滤波电感电容的作用下,可以有效实现直流变换器的输出电压低于输入电压[1]。Buck变换器属于非线性系统,在一些对控制性能要求比较高的场合,传统的PI控制方法无法满足其性能要求。关于使用非线性控制方法控制Buck变换器的研究,近年来已引起了国内外许多学者的广泛关注[2-3]。滑模变结构控制是一种常用的非线性控制方法[4-6],有许多优点,比如良好的动态特性和鲁棒性[7-8]。当Buck变换器系统的负载突然变化时,输出电压可能会有很大的波动。为了减小输出电压的波动,提高系统的控制性能,本文设计了一种基于有限时间观测器的新型快速终端滑模控制器。首先,采用观测器在有限时间内准确估计出负载电阻,然后根据提出的新型快速终端滑模面和双幂次趋近律,设计快速终端滑模控制器。该控制方法可以使得Buck变化器系统具有快速的动态响应速度和较强的抗扰动性能。通过利用MATLAB软件搭建仿真模型,验证了本文所提方法是有效的。
1 Buck变换器模型描述
Buck型变换器的电路原理图如图1所示。
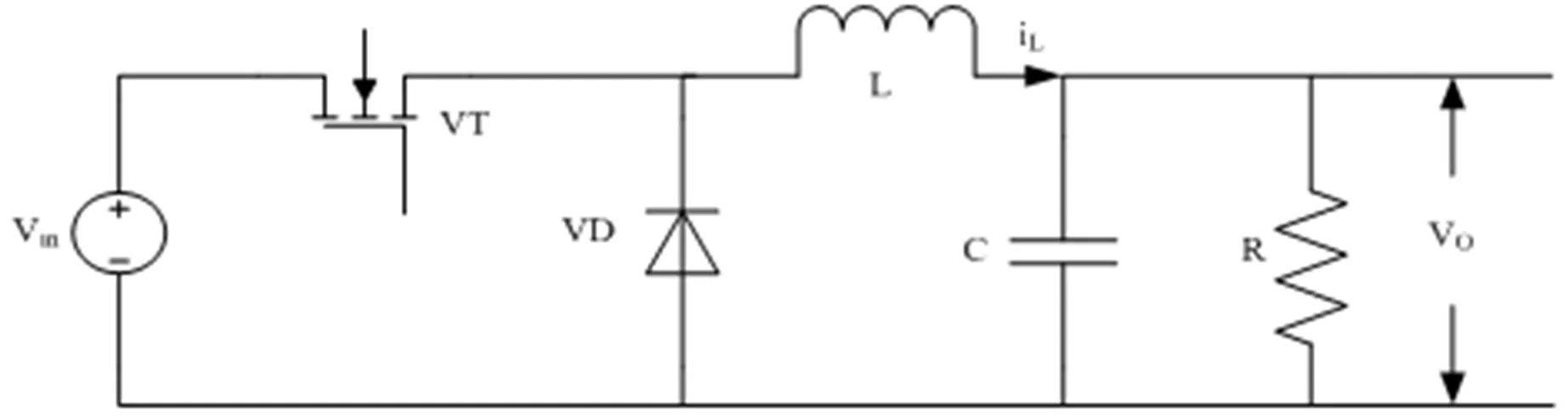
图1 Buck变换器的原理图
图中:Vin为输入电压,VT为功率开关管,VD为续流二极管,L为电感,iL为电感电流,C为电容,V0为输出电压,R为负载电阻。
根据VT的通和断两种工作状态,并利用状态空间平均法,可得出Buck变换器的状态空间平均模型为:
(1)
式中:Vin为输入电压,V0为输出电压,iL为电感电流,C为电容,L为电感,u为控制器的输出。
定义x1=Vref-V0,其中Vref是期望电压值,由式(1)可得出其误差动态方程为:
(2)
本文的研究目标是通过设计基于有限时间观测器的新型快速终端滑模控制器来抑制负载扰动对系统的影响,同时提高系统的动态响应速度。
2 复合控制器设计
2.1 有限时间观测器设计
引理1[9-10]对于下述系统:
(3)
式中:φ>0,0.5<α1<1,α2=2α1-1,通过选择合适的参数k1和k2,可使系统(3)是有限时间稳定的。
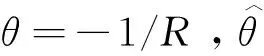
(4)
其中:n1,n2>0,0.5<η1<1,η2=2η1-1。
证明为了分析所设计观测器的稳定性,首先定义观测器误差为:
(5)
由于负载电阻R是一个常数值,因此θ也是一个常数。由式(4)和(5),得出误差状态方程为:
(6)
令:φ=V0/C,则方程(6)可转化为:
(7)

2.2 滑模控制器设计
针对存在负载扰动的Buck型变换器系统,本文拟设计快速终端滑模控制器。
传统的快速终端滑模面可表示为:
s=x2+αx1+β|x1|rsign(x1)
(8)
本文提出的新型快速终端滑模面可表示为:
(9)
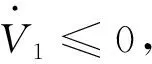
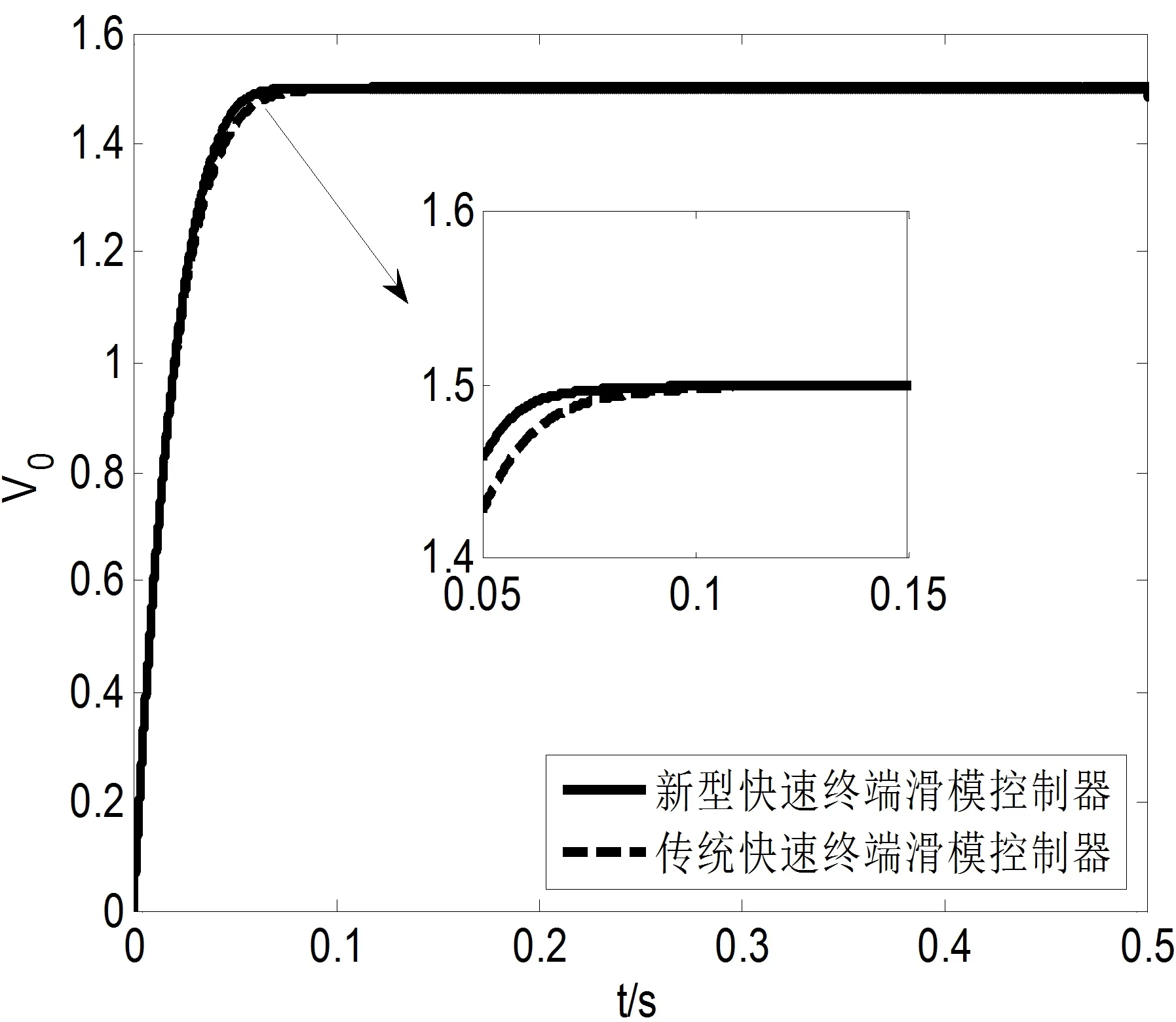
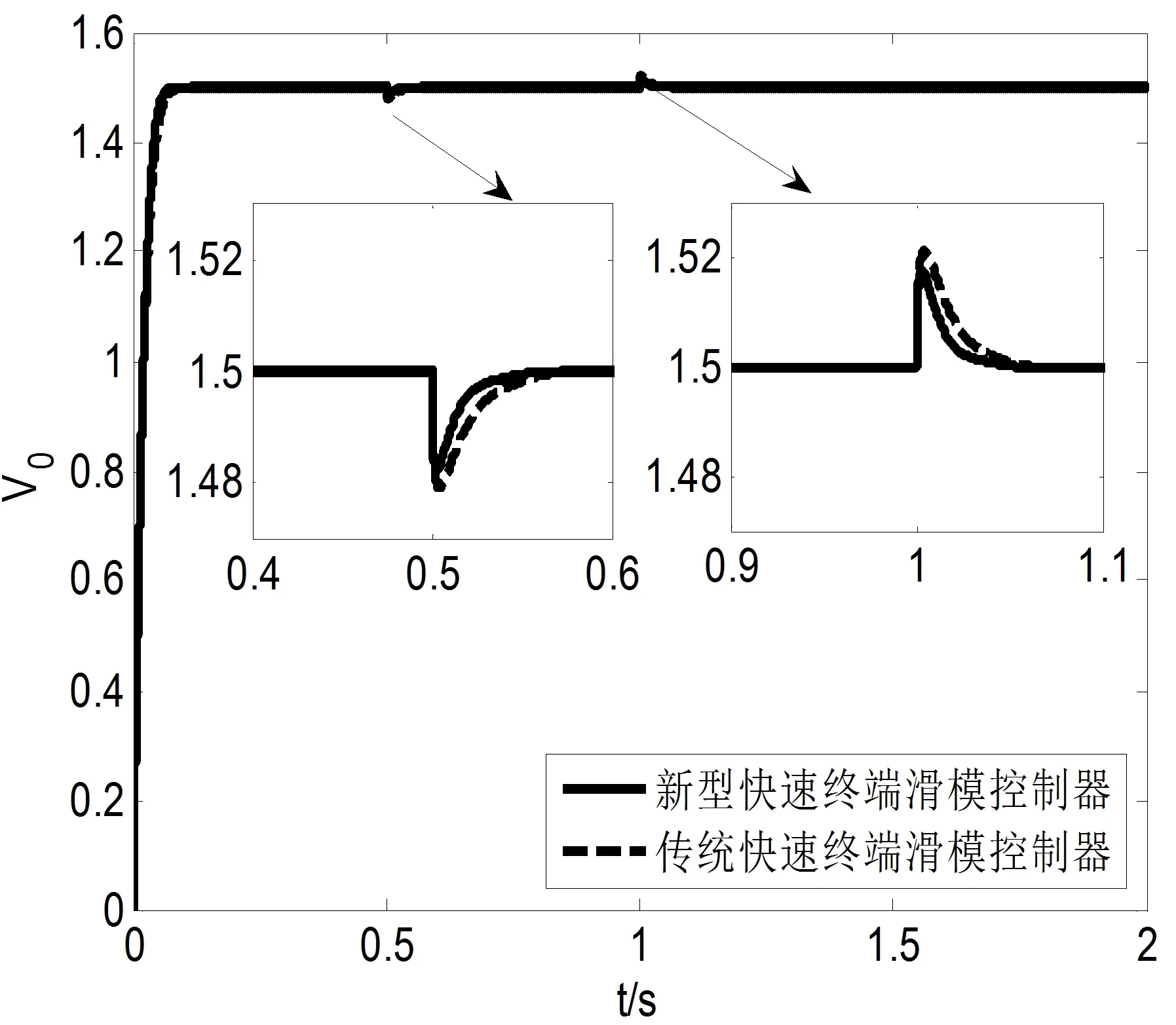
式中:s为滑模变量,α>0,β>0,0 式(9)可写成下面的形式: (10) 对比式(10)和式(8)可知,当|x1|>1时,与传统快速终端滑模面相比,新型快速终端滑模面有着更快的收敛速度。 为了使得趋近运动具有良好的动态品质,本文采用双幂次趋近律,使得滑模变量无论远离平衡点还是靠近平衡点时,控制系统均具有快速的收敛特性。趋近律的表达式如下: (11) 式中:k1>0,k2>0,0<λ1<1,λ2>1。 (12) (13) 定理1针对buck变换器,设计有限时间负载观测器(4)和控制律(12),则系统输出电压误差x1能够快速收敛到平衡点,闭环系统是稳定的。 证明选取Lyapunov函数为: V1=0.5s2 (14) 对(14)进行求导,得: (15) 将式(2)和式(12)代入式(15),得: (16) 接下来,需要证明x1可在有限时间内收敛到0。当s=0时,由式(9),可得: (17) 选择Lyapunov函数V2为: (18) 对式(17)进行求导,得: (19) 将式(17)代入式(19),得: (20) 为了验证本文所提控制策略的有效性和优越性,针对存在负载扰动的Buck变换器系统,利用MATLAB软件的Simulink工具箱搭建仿真模型,并且与其它控制方法进行了对比分析。仿真模型中,Buck变换器参数为:电感L=0.1mH,电容C=1500μF,输入电压Vin=3V,期望输出电压Vref=1.5V。负载变化如下: (21) 有限时间负载观测器如式(4)所示,新型快速终端滑模控制器如式(12)所示,传统快速终端滑模控制器如式(13)所示。仿真结果如图2~3所示。 图2 负载电阻为20Ω时,输出电压波形图 图3 负载电阻变化时,输出电压波形图 由图2可知,在新型快速终端滑模控制器作用下,输出电压收敛到期望电压值的时间在0.07s左右;而在传统快速终端滑模控制器作用下,输出电压收敛时间为0.1s,由此可见,本文提出的控制策略可以使得控制系统具有更快的收敛速度。由图3可知,在新型快速终端滑模控制器的作用下,在0.5s这一时刻,负载电阻从20Ω变为10Ω时,电压跌落了0.018V,恢复时间为0.05s左右;在1s这一时刻,负载电阻从10Ω变为20Ω时,电压上升了0.018V,恢复时间为0.05s左右。而在传统快速终端滑模控制器的作用下,在0.5s这一时刻,负载电阻从20Ω变为10Ω时,电压跌落了0.022V,恢复时间为0.07s左右;在1s这一时刻,负载电阻从10Ω变为20Ω时,电压上升了0.022V,恢复时间为0.07s左右。由此可见,当负载发生突变时,在新型快速终端滑模控制器作用下的系统有着更小的电压变化,以及更好的动态恢复特性。因此,在本文所设计的控制器作用下,Buck变换器系统具有快速收敛特性和良好的抗扰动性能。 本文设计了一种基于有限时间负载观测器的新型快速终端滑模控制器,该控制器可实现对存在负载扰动的Buck型变换器系统的有效控制。通过观测器可以在有限时间内准确估计出负载电阻,再基于提出的新型快速终端滑模面和双幂次趋近律设计一种新型快速终端滑模控制器,该控制策略可有效抑制负载扰动对系统造成的影响,从而提高控制系统的性能。利用Lyapunov定理证明了观测器的收敛性和闭环系统的稳定性。最后,通过MATLAB软件搭建仿真模型,验证了本文所提出的控制策略可以使得Buck型变换器系统的输出电压迅速收敛到期望电压值,并且使得系统具有较强的抗扰动能力。2.3 闭环系统稳定性证明
3 仿真分析
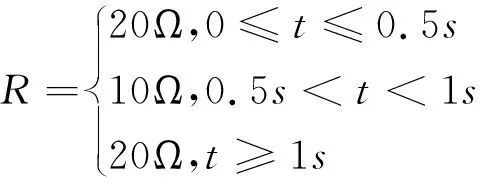
4 结论

