投资者关注能提高市场波动率预测精度吗？——基于中国股票市场高频数据的实证研究

张同辉，苑 莹，曾 文

（1.东北大学工商管理学院，辽宁 沈阳 110169；2.中国科学技术信息研究所，北京 100038；3.瑞士苏黎世联邦理工学院管理技术与经济系，瑞士 苏黎世 8952）

1 引言

投资者对股市信息的关注是导致市场价格波动的前提和基础，“有效市场假说”认为参与市场交易的投资者是“理性、同质的决策体”［1］，投资者关注有限性引发的认知偏差并不会对市场价格波动产生影响。而事实上，由于市场中信息不对称、交易摩擦等问题，大量投资者是非理性、异质的，投资者行为对市场波动的影响并非如经典假设般无足轻重。有限理性的投资者拥有不同的投资偏好、关注不同的市场信息，由此形成了不同的市场认知和未来预期。投资者对市场认知的偏差会通过交易行为反馈到市场价格的波动中。由于大量投资者认知和预期不同而产生的价格波动反映了投资者关注对股票市场的内源性影响。

目前，大多数学者已经认同异质的投资者关注会对股票市场波动产生影响。但受制于投资者关注无法准确衡量，现有研究大多通过定义不同期限的市场累积波动率来模拟异质投资者的行为。突破基于股市历史价格数据研究市场波动的局限，将投资者关注对市场波动的直接影响考虑进市场波动率的相关研究中，不仅对明晰股票市场运行机制有一定的启发性意义，对金融市场的实践也具有重要的应用价值。

现有市场波动率的研究大多基于GARCH 族和SV 族模型。但随着高频数据可获得性的提高，基于日内高频数据研究市场波动率成为学术界和实务界的广泛共识。Andersen和Bollerslev［2］提出的已实现波动率（realized volatility，RV）测度方法和Corsi［3］基于“异质市场假说”构建的异质自回归模型（HAR），逐渐成为普遍接受的市场波动率测度及建模方法。

其后，大量学者分别从对内将已实现波动率进一步分解为连续性波动和跳跃性波动两部分，对外通过引入杠杆效应等其他变量对HAR 模型进行改进。例如：Andersen等［4］基于多种跳跃统计检验方法，建立了HAR-RV-J和HAR-RV-CJ模型，证实了分离已实现波动可以提高HAR-RV 模型的预测表现。Corsi等［5］利用修正的门限多次幂变差提出了HAR-RV-TCJ模型。Corsi和Reno［6］进一步将收益率负向冲击的异质结构引入HAR 模型，构建了LHAR 模型。此外，国内学者马锋等［7］提出两个含跳跃识别检验的符号跳跃变差，宋亚琼和王新军［8］提出考虑跳跃行为及杠杆效应的LHARQ-CJ模型，罗嘉雯等［9］构建包含杠杆效应的HAR 贝叶斯时变模型等，都从内外两个角度对HAR 模型进行了不同程度的改进。

国内外学者关于市场波动率模型的研究已十分丰富，但现有文献均是基于市场交易的历史数据来研究和预测未来市场波动率，即使如HAR 类模型，也未将投资者关注等因素有效的引入波动率模型之中。随着行为金融学的兴起，定量化研究投资者的关注行为，并进一步研究投资者关注对市场的影响成为新的研究热点［10-12］。

传统的投资者关注通常使用涨停板事件［13］、广告费用［14］以及新闻报道［15］等间接代理变量。随着互联网的普及，基于海量在线搜索数据量化投资者关注行为成为新的可能。Da等［16］首次采用谷歌趋势（Google Trends）研究投资者关注，发现与传统间接代理变量相比，搜索引擎的搜索指数可以更直接的反映投资者对股票的关注程度。Aouadi等［17］在个股层面证实了以谷歌趋势为代理变量的投资者信息需求与股票市场流动性存在正向相关关系。Joseph等［18］和Smith［19］的研究均表明，谷歌搜索强度可以可靠地预测股票回报和交易量。Hamid等［20］和Dimpfl等［21］利用谷歌趋势预测道琼斯工业平均指数的波动时也发现，预测的准确性会随着投资者关注的增强而显著提高。Weng等［22］证实了纳斯达克市场上市公司股票具有与市场指数相同的结论。Peilin［23］从跨期网络搜索与市场波动的影响关系出发，指出网络搜索的增加可能预示着市场波动性的增加，并将降低后一期的股票回报率。Dzieliński等［24］进一步研究了投资者关注的非对称性与市场波 动 间 的 关 系 问 题。Yu Lean 等［25］和Guan Hongjun等［26］则从网络搜索角度对市场波动预测问题进行研究，指出与传统波动率预测方法相比，考虑网络搜索数据可以获得更好的预测效果。

然而，与谷歌搜索相比，百度搜索引擎在中国市场具有更为广泛的市场份额，成为研究中国市场投资者关注的重要数据来源。例如，俞庆进和张兵［27］利用百度指数代理投资者关注，发现投资者关注与同期股票收益率之间存在正向相关关系。Fan等［28］的研究也证实基于百度指数的投资者关注对未来市场价格表现存在正向压力。赵龙凯等［29］利用百度指数研究了投资者关注与股票收益率之间的关系，发现高关注股票的收益率要显著大于低关注股票。Wang Xiaolin等［30］基于股指期货市场的研究发现百度搜索在短期内存在反转效应。Shen Dehua等［31-33］通过系列研究证实了百度搜索信息流与市场收益率波动存在显著的领先滞后关系。卫强等［34］通过研究个股的百度搜索量和目标股票价格间的关系，提出了个股层面的交易策略。张谊浩等［35］、Kou Yi等［36］和陈声利等［37］的研究都试图证实基于百度指数的网络搜索量具有预测未来股票市场的作用。

综上所述，目前国内外学者的研究已经证实投资者关注与股票市场具有显著的相互影响关系。但是较少学者深入探讨投资者关注对未来市场波动的预测作用，也未提出系统的研究方法和模型，而且现有研究中投资者关注与市场波动在统计上的强相关性，也无法得出投资者关注就是导致市场波动的影响因素［38］。只有进一步揭示投资者关注是否存在对市场的预测能力，才能更好的理解二者之间的关系，也更具实践意义。基于此，本文以中国股票市场最具代表性的上证指数和深证成指为研究样本，通过聚合多种网络搜索指数数据，分别构建了上证指数和深证成指的投资者关注指标。然后基于时间延迟的去趋势交叉相关性分析（DCCA）方法［39］，克服现有研究中面临的时间序列的不稳定性和非线性特征等问题，深入探究投资者关注和股票指数序列间的交叉相关性及其领先滞后关系。

与以往研究相比，本文的主要贡献在于：首先，本文将投资关注从个股层面转向股票市场的整体，克服了个股层面投资者关注研究面临的噪声交易者和关注度不足的问题。其次，不同于现有利用搜索引擎绝对搜索量或对数处理的形式构造投资者关注指标的方法，本文采用多种网络搜索指数的相对变化率定义新的投资者关注代理变量，不仅弥补了已有方法的部分缺陷，而且在实证研究中验证了新指标的有效性。再次，本文将投资者关注与股票市场的关系研究拓展到非线性的交叉相关性研究，并进一步揭示了二者的传导方向和传导强度，从而为投资者关注融入波动率预测模型扫清了障碍。最后，本文将投资者关注变量引入波动率预测模型，构建了新的投资者关注波动率预测模型，并证实了在投资者高关注时期，引入投资者关注变量可以更加有效的预测中国股票市场。

2 数据选取与描述

2.1 样本选择和数据来源

本文选择2011年1月4日至2016年11月10日上证指数（000001.sh）和深证成指（399001.sz）5分钟高频数据作为研究样本。选择上述研究样本基于以下三点考虑：（1）上证指数和深证成指作为上海证券交易所和深圳证券交易所各自代表性指数，能够充分反映中国证券市场价格波动的整体态势和运行状况。（2）由于沪深两地交易所上市公司规模的不同，上证指数和深证成指可以分别代表大盘股票和中小盘股票的波动性特征，进而提高研究的全面性和稳健性。（3）百度指数提供自2011年1月1日之后的搜索数据，剔除非交易日数据，共可得到1422个交易日数据，这一样本区间涵盖了中国证券市场相对完整的牛熊市波动周期。

上证指数和深证成指5 分钟高频数据来源于Wind数据库，同期的网络搜索数据通过抓取百度指数（http：／／index.baidu.com）官方网站获得。上海和深圳证券交易所每个交易日有4个小时的交易时间，在5分钟的采样频率下，每个交易日内共有48个样本点（不含开盘价）。本文采用已实现波动率衡量股票市场波动，与日收益率平方相比，这种方法可以有效降低噪声及误差对波动率估计量的影响。形式如下：

其中RVsz，t和RV sc，t分别代表第t日的上证指数和深证成指的已实现波动率。

2.2 投资者关注代理变量

本文选择百度指数作为构建投资者关注度代理变量的基础。百度指数是根据百度每日海量用户网络搜索数据整理而成。根据中国互联网络信息中心发布的《中国互联网络发展状况统计报告（2017年7月）》和《2015 年中国网民搜索行为调查报告》及Stat Counter的统计数据，在中国6.09亿搜索引擎用户中，百度搜索的品牌渗透率为93.10%，样本期内百度搜索月均市场占有率为69.03%。此外，上海证券交易所和深圳证券交易所统计年鉴也表明，中国网络搜索用户和股民的地区分布、年龄结构、学历层次具有高度耦合性，这说明百度作为占据市场主导地位的搜索引擎，亦是大多数投资者的首要信息检索工具，因此以百度指数为基础构建投资者关注代理变量具有很好的代表性。

现有文献大多采用百度指数绝对搜索量或对数数据作为投资者关注的代理变量。这种方法存在明显的不足：（1）随着互联网的普及和手机搜索用户的崛起，百度指数经历了井喷式的快速发展，现有文献中采用的绝对搜索量和对数处理的方法已不能满足数据平稳性这一基本假设。（2）相对于搜索量的绝对变化，投资者每日关注的相对变化趋势更能反映百度搜索存量用户对股票市场的关注，因此蕴含了更有价值的关注信息。（3）由于百度指数自身量级的急剧变化，传统方法在模型参数估计方面也面临较大的困难。

此外，上证指数和深证成指作为中国最具代表性的股票市场指数，不同区域投资者的语言偏好不同，可能会使用股指的全称、简称、股指代码等不同关键词进行检索。俞庆进和张兵［27］指出搜索证券简称和证券代码的用户，更可能是潜在的投资者。因此，本文在考虑不同搜索关键词的同时采用了百度指数“需求图谱”功能。该功能提供了样本期内不同搜索关键词之间的关联关系及关联强度。图1展示了以“深证成指”和“399001”为搜索关键词的百度需求图谱。

从图1可以看出：（1）上证指数和深证成指的百度指数搜索关键词具有极强的搜索关联性，这不仅说明沪深两市的投资者具有高度耦合性，也说明将这两只股指成对研究具有理论和实践上的必要性。（2）“深证成指”和“深证指数”也具有较强的相关性，这说明同一股指在不同投资者群体中存在不同的简称。（3）股指简称和股指代码互不为相似关键词，这说明投资者使用百度搜索信息时具有较为固定的搜索习惯，较少投资者混用股指名称和股指代码进行搜索。因此，本文采用股指名称和代码的集合构成相应股指的网络搜索指数。即，以“上证指数”、“000001”和“上证”的百度指数搜索集合定义上证搜索指数（BaiduSVsz），以“深证成指”、“399001”和“深证指数”的百度指数搜索集合定义深成搜索指数（BaiduSVsc）。进一步，通过每网络搜索指数BaiduSVt的相对变化率定义投资者关注度代理变量（BIt）：

其中BaiduSVi，t表示从百度指数获取的第i只股指的第t日的网络搜索指数。

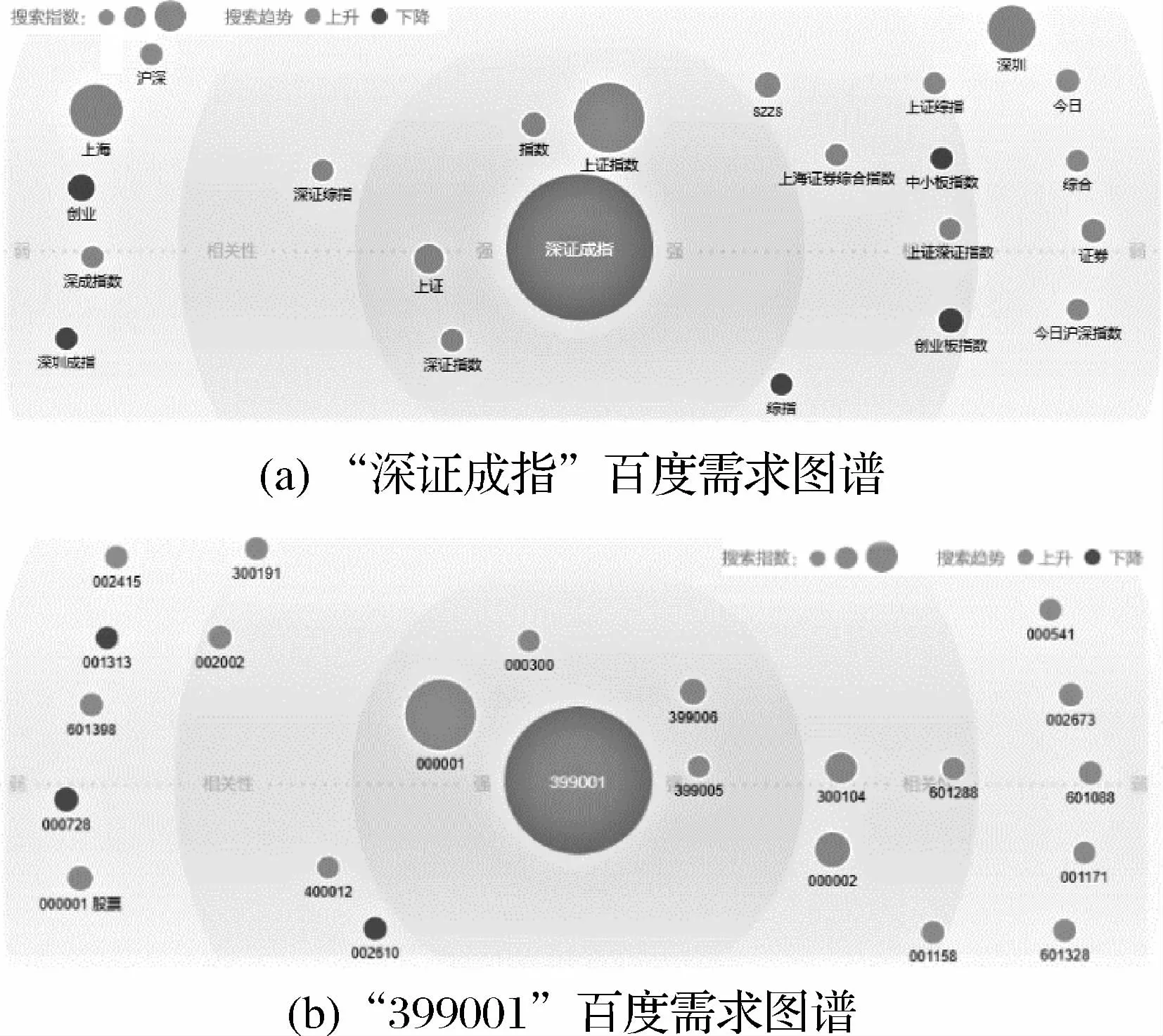
图1 百度搜索关键词需求图谱

2.3 数据描述

通过对样本期内上证指数和深证成指市场表现的考察，本文以2014年10月28日为节点将样本数据划分为两个子区间。图2是上证指数已实现波动率和搜索指数的双坐标图，表1为样本指数的基本统计特征。

从图2可以看出，上证指数在样本期内的已实现波动率和搜索指数具有高度正向同步性，市场高涨时期的投资者网络搜索指数也显著升高，市场低迷时期的投资者网络搜索指数也在低位震荡徘徊。因此，根据市场波动强度和投资者关注水平划分样本区间，进而研究投资者关注与市场波动态势间的影响关系，可以更好的揭示二者之间的相互作用机制。

由表1可知，在样本期二时期，上证指数和深证成指已实现波动率的均值、标准差均显著高于样本一时期，说明沪深证券市场的波动强度在两个子时期发生了改变。此外，样本期内的已实现波动率序列的偏度和峰度表明，与正态分布相比其形态表现为右偏性及尖峰特征；通过Jarque-Bera统计量也可以看出，波动率序列在1%的显著性水平下拒绝了正态分布的假设；ADF 单位根检验和滞后5、10、22期的Ljung-BoxQ检验表明，已实现波动率序列是存在自相关特征的平稳序列。在两个子样本期内，投资者关注大部分的描述性统计特征与已实现波动率相似，也是存在自相关特征的非正态分布的平稳序列。

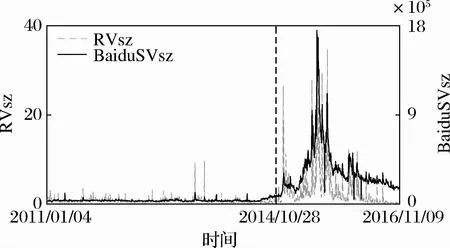
图2 上证指数已实现波动率和搜索指数双坐标图

表1 样本指数已实现波动率和投资者关注统计量

3 投资者关注与市场指数的关系研究

本文采用基于时间延迟的DCCA 方法判定投资者关注和市场指数波动之间的影响关系及传导方向。该方法在DCCA 方法的基础上引入时间延迟变量τ，可以更好的判定不同时滞下序列的交叉传导方向和领先滞后关系。为了更加清晰的展示各序列的传导方向，参照文献［40］定义传导强度指标，形式如下：

图3和图4分别是样本指数与投资者关注在不同时滞下的交叉相关关系图。

图3 不同时滞下上证指数与投资者关注交叉相关性图

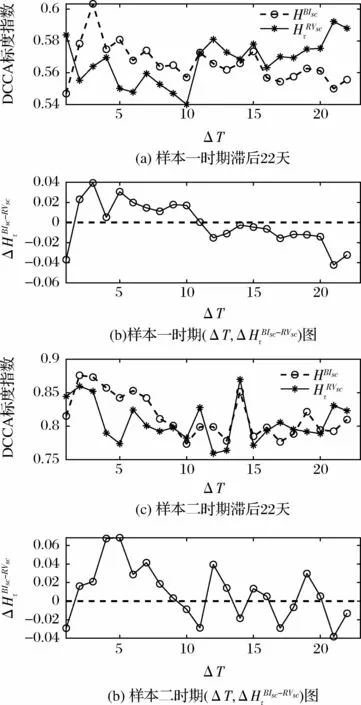
图4 不同时滞下深证成指与投资者关注交叉相关性图

从图3（a）、（c）和图4（a）、（c）可以看出，已实现波动率和投资者关注滞后1～22日的标度指数均大于0.5，表明二者之间存在显著的长程相关性；而且，在第二个样本时期内的标度指数均显著高于第一个样本时期，表明随着市场指数波动性的提高和投资者关注的显著增强，这一时期表现出更强的联动性特征。从图3（b）、（d）和图4（b）、（d）可以看出，当滞后1 期时，两个样本区间的和都显著为负，表明市场指数波动对投资者关注的影响更强；同时，在两个样本区间内，随滞后阶数的增加呈现衰减趋势，说明随着市场波动时滞和投资者关注时滞的延长，投资者关注与市场指数波动间相互影响逐渐减弱，这可能是因为投资者进行交易决策时更加关注短期内的市场信息和市场波动，受中长期市场表现的影响较小；此外，第二个样本时期内高于基线（零线）的数量要明显多于第一个样本时期，这说明在市场波动更为剧烈的时期，投资者关注对市场指数的波动存在更为持久的影响。

综上，投资者关注与市场指数波动存在显著的相关性，当投资者关注（市场指数波动）滞后时，会对当期市场指数波动（投资者关注）产生影响，并且这种影响会随着滞后期的增大而逐渐衰减。因此，二者之间的传导是双向的。但是，从传导强度来说，投资者关注对市场指数波动的传导要始终强于反向的传导，而且传导强度随着市场波动性的提高而显著增强。

4 实证模型与结果分析

4.1 波动率预测标的模型

ARMA 模型是一种较为成熟的波动率预测模型，由自回归（AR）和移动平均（MA）两部分构成，标准的ARMA（p，q）模型如下：

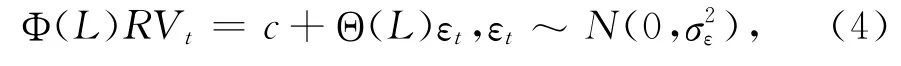
但是，ARMA 模型没有考虑金融资产普遍存在的长记忆性，即波动序列的自相关性；而ARFIMA模型中AR 部分表现出的缓慢的双曲线衰减过程可以较好模拟波动时间序列的自相关行为，本文沿袭Andersen等［41］的建模思路，采用ARFIMA 模型对已实现波动率建模，ARFIMA（p，d，q）模型如下：

其中（1-L）d代表分数差分算子，μ为母体均值。

Corsi［3］将交易者分为三类：日交易者，周交易者及月交易者，分别代表短期、中期和长期交易，建立了HAR-RV 模型。HAR-RV 模型既具有长记忆特征又体现了波动信息异质性，形式如下：

其中RV t、RVt-5和RV t-22分别代表日、周和月的已实现累积波动率。

Andersen等［4］的研究表明，将已实现波动率分解为持续性部分和跳跃性部分，进而构造HARRV-J模型和HAR-RV-CJ模型，可以显著提高HAR-RV 模型的预测精度。这两种模型的表达形式如下：

其 中J t= max（RV t-BPV t，0），BPV t=是标准正态分布随机变量Z绝对值的均值；Ct=I（Zt≤Φa）·RV t+I（Zt≥Φa）·BPV t，CJ t=I（Zt＞Φa）·［RV t-BPV t］，I（·）是示性函数。

为了考察“杠杆效应”对未来波动的非对称性影响，Corsi等［6］引 入变 量 来 构建了LHAR-RV 模型，其表达形式如下：

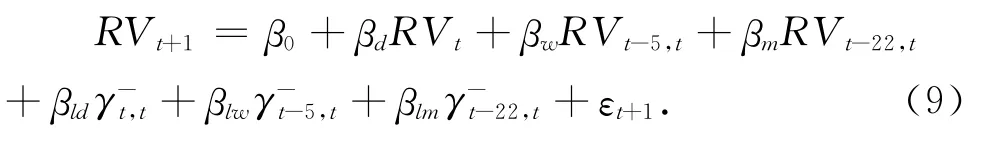
4.2 投资者关注波动率预测模型

从前文投资者关注与市场指数的关系研究可知，滞后的投资者关注对市场指数具有更强的影响。因此，对已有模型的一种自然改进就是将投资者关注变量BI t加入已有模型。

本文首先将投资者关注变量引入ARMA 类模型，在ARMAX 和ARFIMAX 模型范式的基础上，分别建立ARMA-BI（p，q，b）模型和ARFIMABI（p，d，q，b）模型。以ARMA-BI为例，在ARMA 模型回归中引入滞后b阶的投资者关注变量BI t，具体形式如下：

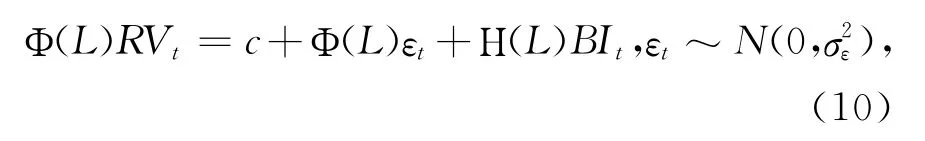
其中H（L）=η1L+…+ηb L b代表滞后b阶的滞后算子。

随后，本文进一步将代表投资者累积关注的BI t、BIt-5和BIt-22变量引入HAR 模型，分别建立HAR-RV-BI、HAR-RV-JBI、HAR-RVCJBI、LHAR-RV-JBI和LHAR-RV-CJBI共5种投资者关注模型。为了更加清晰的表示HAR类模型，在下文中均省略模型名称中的RV 部分，即上述5种改进模型在下文中分别简写为HAR-BI、HAR-JBI、HAR-CJBI、LHAR-JBI和LHARCJBI。以HAR-BI模型为例，其形式如下：

4.3 参数估计

表2和表3分别是上证指数ARMA 类模型和HAR 类模型的参数估计结果。由于与上证指数结果相似，为节省篇幅，本文省略了深证成指的参数估计结果。

从表2和表3 可得到如下结论：（1）从表2 可知，ARFIMA 模型分整参数d的估计值显著大于0，说明与ARMA 模型相比，ARFIMA 模型可以更好的拟合样本序列具有的显著长记忆性和分数维单整性质。（2）从表3可知，代表短期、中期和长期已实现波动率的参数（βd、βw和βm）在大部分情况下都是显著的，说明市场波动存在很强的持续性。此外，通过对比两个样本时期参数显著性可以发现，市场的跳跃行为和“杠杆效应”在第二个样本时期更为明显，说明在市场波动较剧烈的阶段更易发生并捕捉到上述行为。（3）综合比较两表的拟合优度R2可知，预测模型在第二个样本时期内的样本拟合能力要显著优于第一时期。在第一个样本区间内，ARMA 类模型的样本拟合能力要稍逊于HAR 类模型；在第二个样本区间内，ARMA 类模型的样本拟合能力大幅提升，尤其是ARFIMA-BI模型的R2超过本时期内的其他预测模型。（4）对比包含投资者关注变量的改进模型和原始模型的参数估计结果可知，改进模型的拟合效果要明显优于原始模型。通过观察投资者关注变量的t统计量值和显著性水平也可以发现，除样本期一的上证指数HAR-BI模型外，其他改进模型中投资者关注变量的参数估计结果（η和βbid、βbiw、βbim）至少存在一个在10%的显著性水平上显著；而且，投资者关注变量的参数显著性水平在样本期二内显著提升。因此，投资者关注变量的加入更好的解释了股票市场的波动性特征。

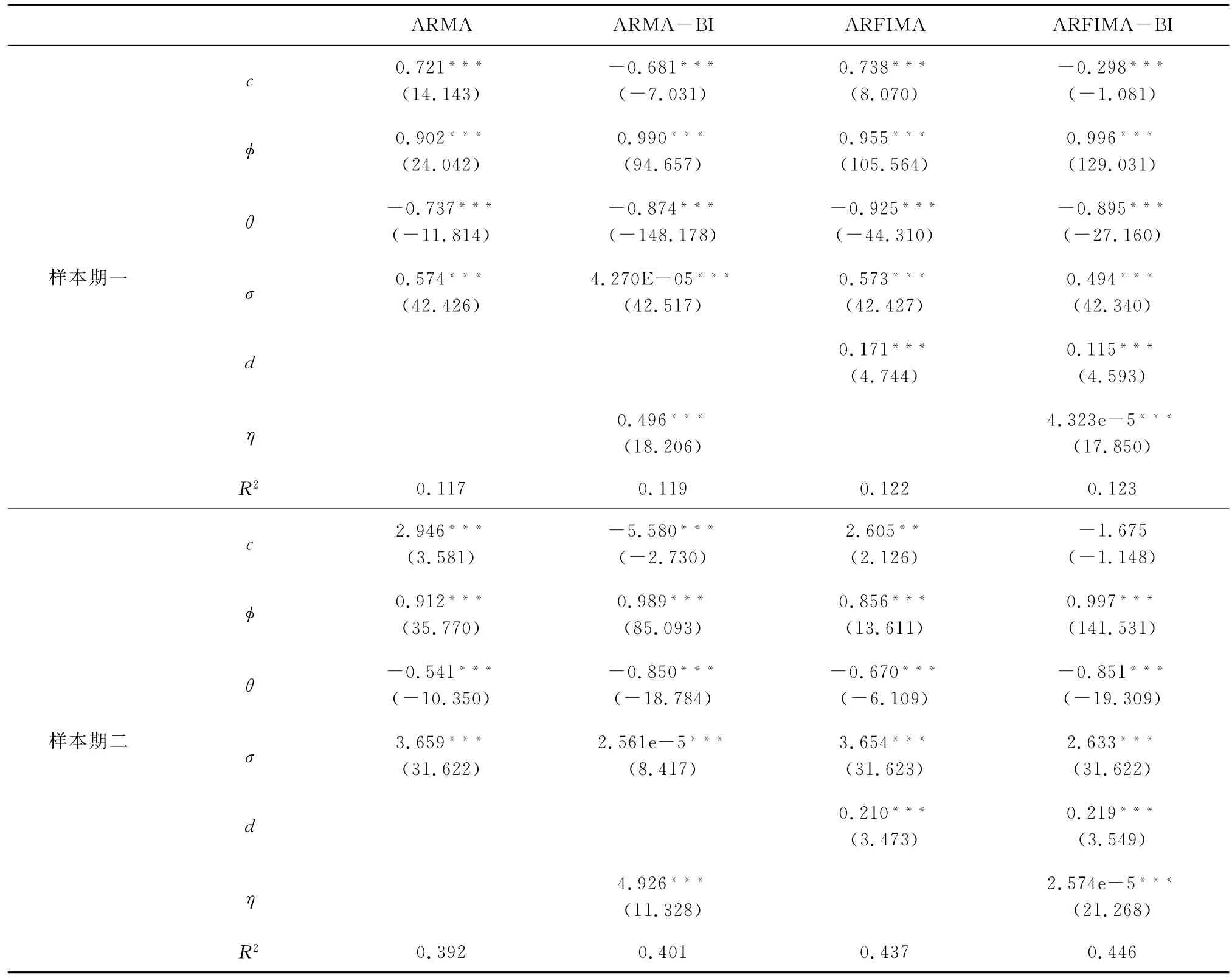
表2 上证指数ARMA类模型参数估计结果

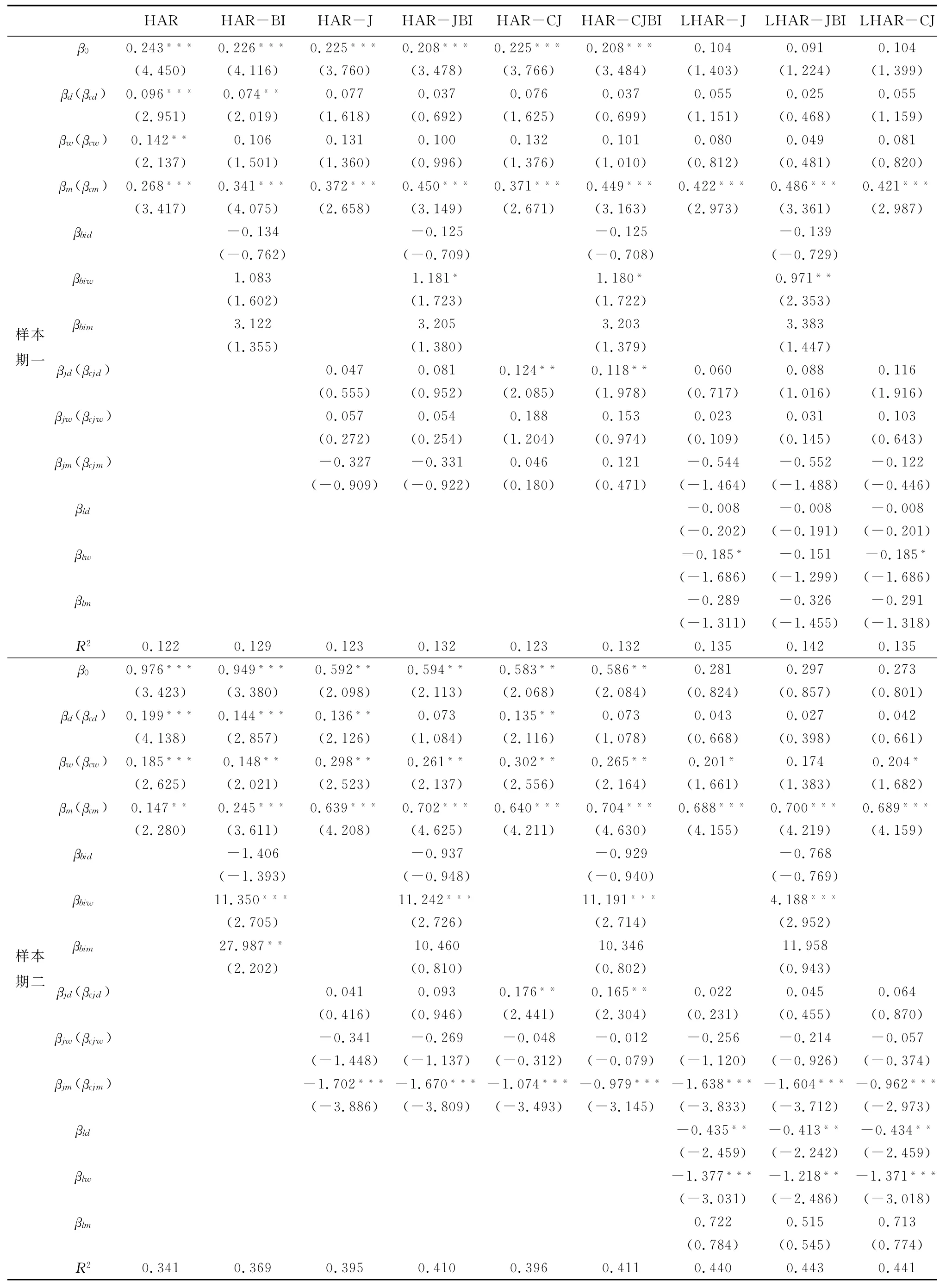
表3 上证指数HAR 类模型参数估计结果

4.4 样本外预测及MCS检验

为进一步研究上述波动率模型的预测能力，本文采用“滑动时间窗”的样本外预测方法，将样本区间的前80%划分为估计样本，将余下的20%作为保留样本。此外，由于目前对波动率预测模型的评价标准尚未有统一意见，因此本文采用了5种广泛使用的损失函数指标作为判断模型预测精度的标准。形式如下：

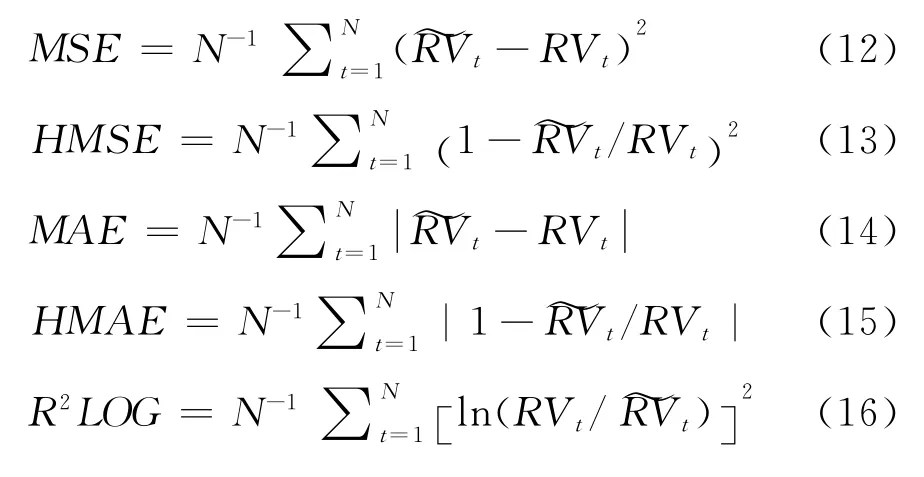
与此同时，为进一步增强检验结果的稳健性，本文采用“模型信度设定”（MCS）检验［42］方法来提高检验结果的准确性。样本指数的MCS检验结果分别在表4和表5中列示。

从表4可知：（1）不论在何种损失函数标准及MCS统计量下，除ARFIMA 模型的T SQ统计量外，其他ARMA 类模型都被检验剔除（p值小于0.1），即这两类模型的预测效果明显弱于HAR 类模型。（2）对比表中包含投资者关注变量的改进模型和原始模型的检验结果可知，总体来说，幸存的改进模型和原始模型的数量并未有显著差异；但是，原始模型的损失函数值普遍低于改进模型，其对应的p值也普遍高于改进模型。因此，在第一个样本时期，加入投资者关注变量的改进模型并未表现出显著的改进作用。（3）HAR-J、HAR-CJ、LHAR-J 和LHAR-CJ在14种模型中的波动率预测效果较为突出，每个模型至少在一种损失函数标准和MCS统计量下获得了最小的损失函数值和最大的p值（p=1）。这一结果有力地证明了HAR 类模型在市场走势的平稳时期具有良好的预测能力。进一步，LHAR-CJ模型和LHAR-J模型各自在3 种损失函数标准（LHAR-CJ：MAE、HMAE、R2LOG，LHAR-J：HMSE、MAE、HMAE）及对应的MCS统计量（p=1）下，被检验为样本指数预测值的最优模型。因此，与其他模型相比，这2种波动率预测模型的优势更为显著。这也说明，虽然同处于第一个样本时期，上证指数和深证成指的波动特征也存在细微的差异。

从表5可知：（1）与第一个样本时期相比，ARMA 类模型在本时期的预测能力显著提升。尤其是加入投资者关注变量的ARFIMA-BI模型，在五种损失函数标准和MCS统计量下获得了最小的损失函数值和最大的p值（p=1）；此外，上证指数的ARMA-BI模型也在MAE 标准及对应的MCS统计量下，表现出更优的预测能力。这说明，市场的剧烈波动吸引了更多投资者的加入，大量投资者在网络上搜索市场信息使投资者关注变量的信息含量更为充分，因此加入投资者关注变量BIt可以显著改善模型的预测能力。（2）通过10种HAR 类模型的检验结果可知，总体来说，HAR 类模型的预测能力要稍弱于ARMA 类模型；同时，加入投资者关注变量的改进模型的表现要稍强于原始模型，这一特征在MAE、HMAE 和R2LOG 三种标准下更为突出（改进模型的损失函数值更小）。因此，虽然在市场平稳时期的原始HAR 类模型表现出更优的波动率预测能力；但是随着市场逐渐从低谷期走向繁荣期，股市的繁荣吸引了众多投资者的强烈关注，所以在本时期内加入投资者关注变量的改进模型可以获得比原始模型更优的样本外预测效果。

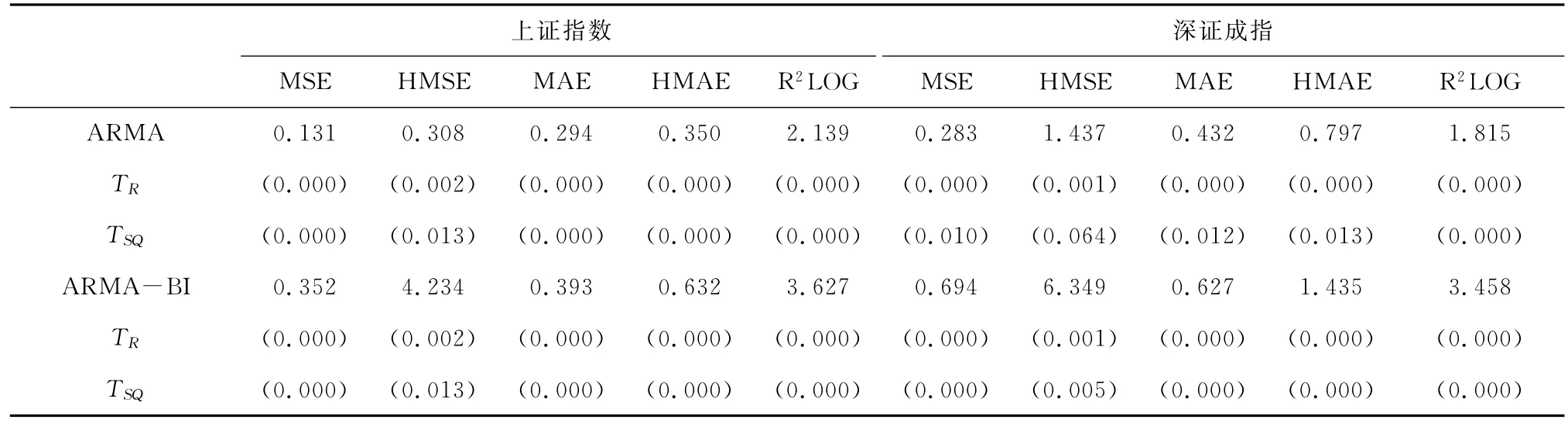
表4 上证指数和深证成指在样本一时期的损失函数及MCS检验结果

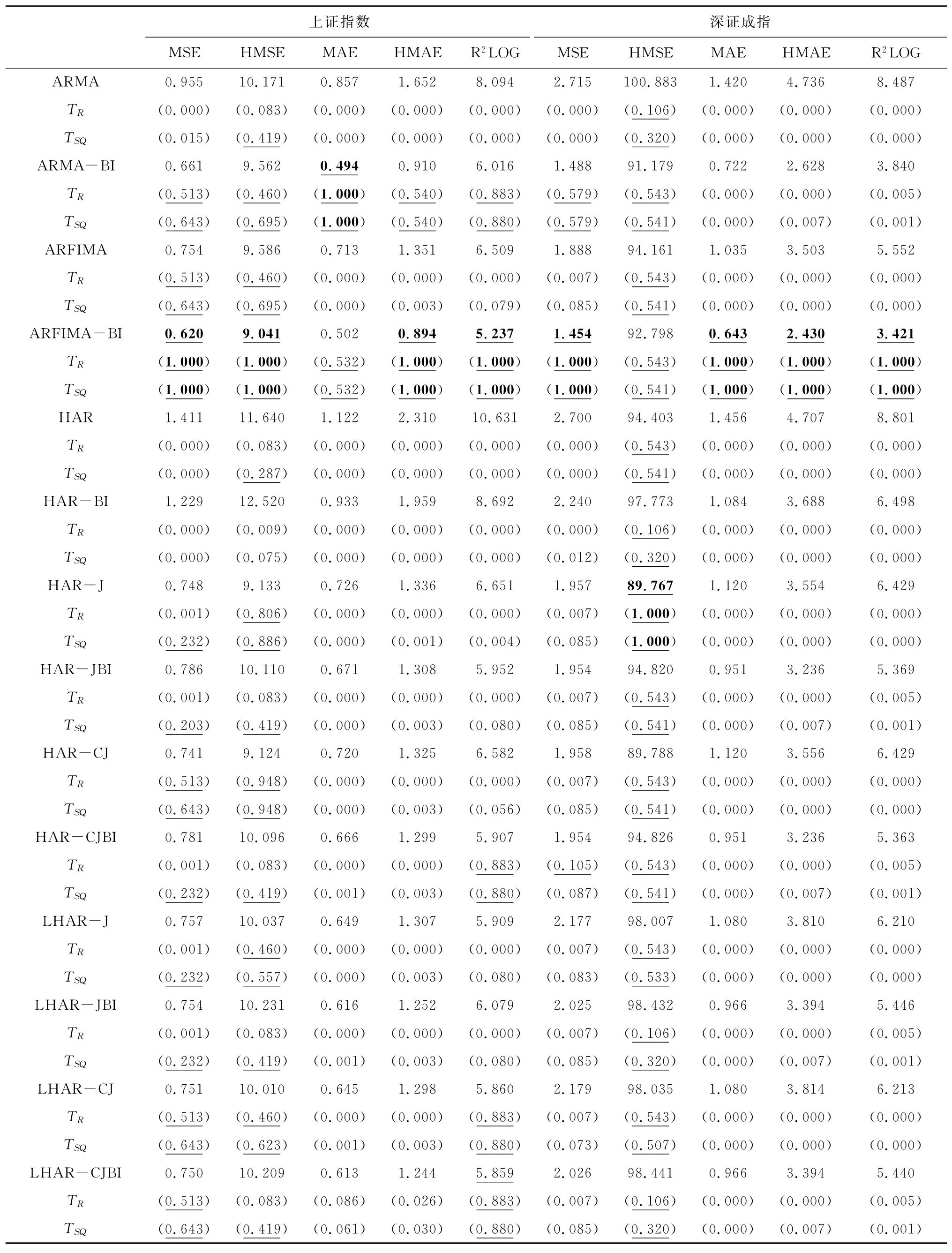
表5 上证指数和深证成指在样本期二时期的损失函数及MCS检验结果

注：表中数字为损失函数值，每种损失函数下的最小值用加粗表示；MCS检验的显著性水平设定为90%，表中括号内数字为进行了10 000次Bootstrap模拟的MCS检验p值，p值大于0.1（加粗和下划线的数字）表示对应模型通过MCS检验，TR和T SQ分别为范围统计量（Range statistic）和半二次方统计量（Semi-quadratic statistic）。

4.5 稳健性检验

本文采用连续等级概率评分（CRPS）方法来进一步检验实证结果的稳健性。CRPS方法可以突破正态分布的假设限制，并且考虑到了分布的位置和形状特征，在风险度量、资产配置等众多对波动分布形态更为关注的领域，拥有更好的预测评价能力。CRPS衡量的是预测值与实际值累计分布函数的绝对误差平均，具体形式如下：

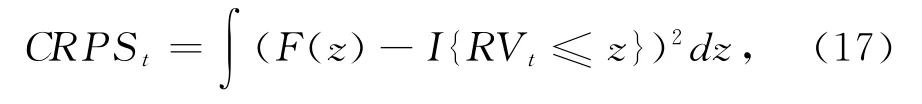
其中F为累计分布函数，I｛·｝是示性函数。CRPS是负导向的评分方法，即CRPS值越小，说明模型的预测精度越高。样本指数的检验结果在表6中列示。

从表6可以看出，CRPS与MCS的检验结果基本一致，HAR 类模型和ARMA 类模型在两个样本时期依次显示出更优的预测能力。通过观察成对排列的改进模型和原始模型，原始模型的CRPS值在样本一时期均低于改进模型，而在样本二时期高于改进模型。此外，在CRPS检验中，LHAR-CJ和LHAR-J模型分别为上证指数和深证成指在样本期一的最优模型，ARFIMA-BI模型为上证指数和深证成指在样本期二的最优模型。上述结果不仅证明了MCS检验结果的稳健性，而且进一步验证了投资者关注变量在市场剧烈波动时期具有更为优异的预测能力。

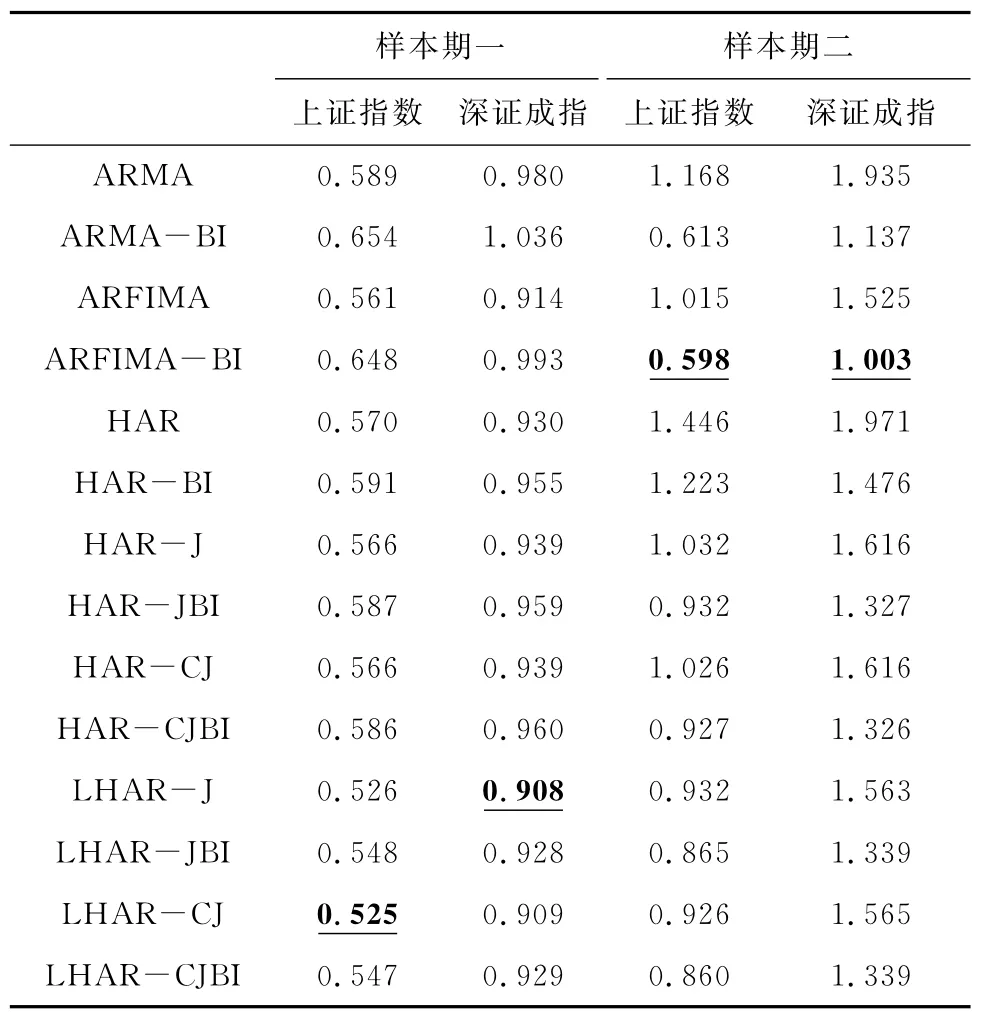
表6 样本指数CRPS检验结果

5 结语

本文基于百度指数定义了新的投资者关注代理变量，以中国股市最具代表性的上证指数和深证成指为研究样本，建立了新的投资者关注波动率预测模型。本文研究结果表明：投资者关注不仅可以提高现有波动率预测模型的样本内拟合能力，而且在投资者高关注时期，投资者关注可以显著且稳健的提高波动模型的样本外预测能力。

本文的研究结果具有重要的实践意义。考虑到中国的网络规模和网络用户已跃居世界第一，在互联网的覆盖广度和使用深度方面，具有其他国家无法比拟的独特优势。而搜索引擎作为基础的网络服务，记录和保存了海量的信息检索数据。充分挖掘这些检索数据隐含的金融价值，对投资者来说，可以“先人一步”的把握市场发展趋势，增加获利机会；对监管部门而言，可以更加高效的监控市场动态，强化市场监管绩效，加快形成完备有效的股票交易市场。