基于遗传回声状态网络的房颤F波提取
张文燕,刘 明,李 鑫
(河北大学 电子信息工程学院,河北 保定 071000)
0 引 言
1 回声状态网络
ESN作为一种新型的递归神经网络,在训练过程中只需要求解输出权值,因此训练速度快,不易陷入局部最优解。且ESN具有的非线性传递函数特征恰好可以将时序信号中的波形特征提取出来,尤其是心电信号中QRST复合波位置的提取。基于遗传算法优化ESN网络的特征提取算法,将远离心脏电极的F波不明显的V5、V6导联,作为ESN网络的参考信号,训练ESN网络,获得完整QRST波形,在房颤明显的V1导联信号上消除得到F波。
储备池是ESN的核心部分,因为它的稀疏连接特性以及它只需要更新输出权值矩阵Wout而其它权值矩阵(输入权值矩阵Win以及内部权值矩阵W)生成就不变的特性,所以ESN特别适用于顺序处理数据,实现房颤实时短数据处理。而在房颤提取方面的主要思想是通过参考信号驱动ESN并在整个训练周期内将其非线性变换收集到储备池状态响应信号中对ESN进行训练,生成不断变化的复杂动态空间,然后通过状态响应信号的线性组合去逼近目标向量。基于ESN的房颤F波提取流程如图1所示。

图1 基于ESN的F波提取
2 基于回声状态网络的F波提取
ESN的输入信号X(n)的表达式如下
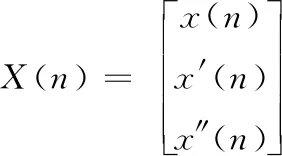
(1)
其中,x(n) 为当前时刻的含有少量房颤的心电信号;x′(n) 及x″(n) 分别是当前心电信号的一阶导数信号和二阶导数信号。
ESN输出信号y(n)为构建后的心室信号,定义如下
(2)
其中,激活函数g(·), 为了降低复杂度,适应实时提取要求,选为恒等函数;其中变量v(n)的表达式为
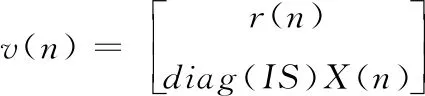
(3)
而r(n)是储备池的状态响应向量,IS是输入信号缩放因子。
(n)=e(n)=x1(n)-y(n)
(4)
式中:x1(n)为房颤明显的V1导联,y(n)为心室信号。
因此,在训练中需要更新Wout和r(n),使滤波后的心室信号y(n)不含心房信号,房颤F波(n)能够准确提取。
输出权值矩阵Wout的更新采用结合最小二乘预白化过程的递归最小二乘算法。其中预白化的过程定义为
z(n)=ψ(n-1)v(n)
(5)
u(n)=ψ-1(n-1)z(n)
(6)
式中:ψ(n)为v(n)的相关系数矩阵的逆矩阵,而ψ(n)的更新如下所示
(7)
(8)
设定Wout(0)=0, 则输出权重的更新为
(9)
而储备池状态的更新公式为
r(n)=(1-α)[f(Wr(n-1)+Winu(n))]+αr(n-1)
(10)
式中:输入权值Win为4×N的矩阵;储备池内部权值W为N×N的矩阵;为了将输入信号非线性地收集到储备池,储备池的激活函数f(·) 的选择为非线性的tanh(·) 函数;遗忘因子α和λ分别采用值为0.8和0.999,均为小于1的正数。
3 利用遗传算法网络调参
基于ESN的消除QRST复合波得到F波的重要步骤是选择ESN储备池初始参数,决定了回声状态网络的提取性能。储备池规模参数N与网络的复杂程度和精确度成正比,N越大QRST的构建越精确,计算程度越复杂,甚至过大会产生过拟合的情况,所以本文采用固定参数100;储备池矩阵的谱半径(spectral radius,SR)由W最大绝对特征值定义,并与确保稳定性的回波状态属性相关,一般在 [0,1] 范围内取值;输入缩放因子(input scaling,IS)作为一个尺度因子,将输入信号驱动到激活函数的非线性区域,在[0,1]范围内取值;储备池稀疏程度(sparse degree,SD)为储备池所含连接的个数,决定着网络的丰富程度,可以降低储备池的计算复杂度,取值范围为[0.05,0.2]。传统遗传算法优化ESN往往计算量大,迭代时间长,不能达到实时获取的要求[10]。进而对遗传算子在选择机制,交叉概率以及变异概率方面进行改进,用于加快进化速度和扩大搜索范围。
3.1 个体编码及适应度函数的选择
因为网络参数的取值范围比较小,所以采用实数编码方式
pop=[SR,SD,IS1,IS2,IS3]
(11)
将目标函数标准均方误差NMSE的倒数作为适应度评价函数,公式如下
(12)
其中,s(n)为心电信号中添加的原始F波,(n)为网络估计得到的F波。
3.2 遗传算子
在亲代选择操作中,根据适应值排序得到最优、优、良、中、差这5个等级的个体,除最优的两个个体直接遗传至下一代外,另外4个等级按2∶1∶1∶0的比例进行交叉和变异操作得到新的个体遗传至下一代。
设计自适应交叉概率以及变异概率,可以有效加快个体的进化速度,同时兼顾扩大搜索范围的要求,如下式所示
(13)
式中:p0和p分别为初始概率和得到的自适应概率;fmax、fav和fmin分别为每一代个体的最大适应度值、平均适应度值和最小适应度值;μ和n都为系数因子。参数ε的随机生成保证了搜索范围的要求,当ε 当平均适应度值接近最大适应度值时,自适应的概率快速增大,需要交叉变异的概率范围就会缩小,从而加快完成进化;反之则自适应的概率变化较小,需要继续交叉变异生成新的个体。图2为本文自适应遗传算法的具体流程。 图2 本文自适应遗传算法的具体流程 在正常心电信号上叠加已知F波得到仿真房颤信号,可以量化估计算法的可行性与准确性。第i导联仿真F波的生成模型可以由以下公式取得 (14) 其中,谐波个数M-1,基频w0=2πf0, 最大频率偏差Δf,调制频率w=2πff, 幅度bm(n)由下式给出 (15) 其中,a表示锯齿幅度,Δa表示调制幅度,wa=2πfa表示幅度调制频率。各参数设置见表1,向量A表示V1、V5和V6导联的幅度峰值,A=[0.150,0.020,0.020]mV。 表1 本文中仿真房颤F波的参数设置 选取MIT-BIH中PTB心电数据库中的10个健康对照组,每组120 s数据,采样频率为1000 Hz,重采样为 250 Hz 作为实验数据。在存在QRST形态固有变化的正常心电数据上,去除P波[13]叠加仿真F波,生成仿真房颤信号用于仿真实验的提取。如图3所示,图3(a)为去除P波之后的心室成分,图3(b)为仿真F波,图3(c)为仿真房颤信号。 图3 仿真房颤信号 在应用自适应遗传算法时,经反复实验,为了得到最优结果设定变量个数为5,种群规模为100,而初始交叉概率与初始变异概率分别为0.6和0.01,其它参数设定为μc=0.3,μm=0.2,nc=nm=2, 终止代数为50[12]。得到284号数据的最优参数为:SR=0.95,SD=8,IS1=0.989,IS2=0.780,IS3=0.685。 在研究心拍个数L对各个算法所提取的F波的准确度的影响时,在表2中可以看到GA-ESN算法随着心拍个数L的变化最小,而其它两种算法变化相对较大。ABS算法(图4(b))、WABS算法(图4(c))以及GA-ESN算法(图4(d))在时域图上的F波提取效果与原始仿真F波(图4(a))的时域对比结果如图4所示。 表2 不同算法的标准均方误差随心拍个数L的变化 图4 仿真F波及用3种算法所提取的F波 图5表示对10个仿真信号分别在随机初始化和遗传算法调参的情况下,运行20次所得到的结果对比图,用平均值±标准差来表示数据的离散程度。 图5 遗传算法优化回声状态网络对NMSE的影响 在真实房颤信号中提取F波时,因房颤信号中房颤F波与心室信号的频率范围不同,所以可以采用频谱集中度(spectral concentration,SC)来衡量提取算法的有效性。房颤F波的提取性能越好,QRST消除性能越好,频谱集中度SC则表现出越高的数值,定义请参见文献[5]。 自MIT-BIH中的PTB数据库中取5例房颤病人的 120 s 心电图数据作为实验数据。分别为153号、201号、254号、257号、286号。ABS算法、WABS算法与GA-ESN这3种算法所提取导联中F波的中心频率f0和频谱集中度SC见表3。图6(a)和图6(b)分别为原始房颤心电信号和ESN重建的心室信号,而图6(c)为本文算法所获得的F波,图6(d)为ABS所提取的F波(本文以153号数据为例)。 表3 不同算法所提取的F波的频谱集中度(SC) 图6 原始房颤信号所得心室信号及GA-ESN算法和 ABS算法所得F波 由表2可以看出,GA-ESN算法相对ABS算法、WABS算法,从所提取F波的标准均方根误差NMSE可以看出,前者的受心拍个数的影响较小,而后两者所受的影响较大。而L=10时NMSE较大的原因在于数据采集时引起的瞬变,所以对计算误差有一定的影响。因此GA-ESN算法相比于传统的QRST模板生成方法在处理短数据段方面有一定优势。图4所示的时域实验结果更加直观地反应了GA-ESN算法相比与其它两种算法的优越性。图5结果表示遗传算法调参的情况下,不仅结果准确性有所提高,而且数据的离散程度不大,结果更稳定。 反映F波的提取质量的频谱集中度(SC)作为真实房颤信号的提取指标取得了较好的效果。表3中的SC表明,GA-ESN相比于ABS和WABS所提取的频谱集中度均有一定程度的提高,而在房颤F波振幅小(比较难提取)的257号数据上频谱集中度同样得到提高,提取效果更好。图6 F波时域波形对比更加形象直观地验证了GA-ESN算法相比于ABS算法更加有效,进一步验证了GA-ESN算法在真实房颤心电信号中提取F波的准确性。 本文提出一种基于遗传回声状态网络来提取房颤F波的方法,网络参数由自适应遗传算法来调整,再利用不同导联之间的生理差异性来消除QRST复合波,既保证了房颤F波的提取稳定性,又提高了房颤F波的提取准确度。经验证,采用遗传回声状态网络来提取房颤F波相比于ABS算法和WABS算法,对仿真房颤信号提取出来的F波的标准均方根误差均有不同程度的降低;对真实房颤信号F波的提取准确度也明显提高。本算法在短时数据段上有效提高了房颤F波提取的准确性,为远程便携式心电监护系统的研究提供了可靠基础。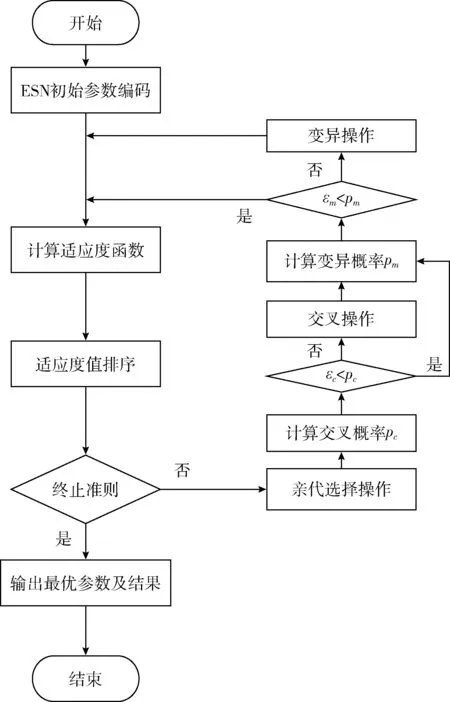
4 实验分析
4.1 仿真房颤F波的提取

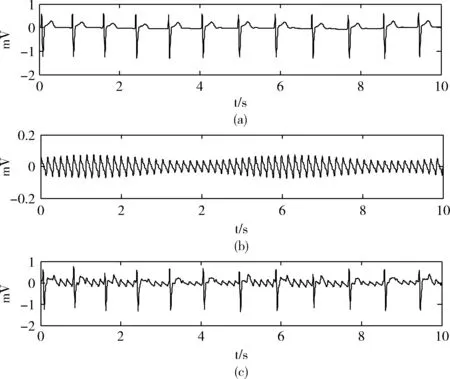

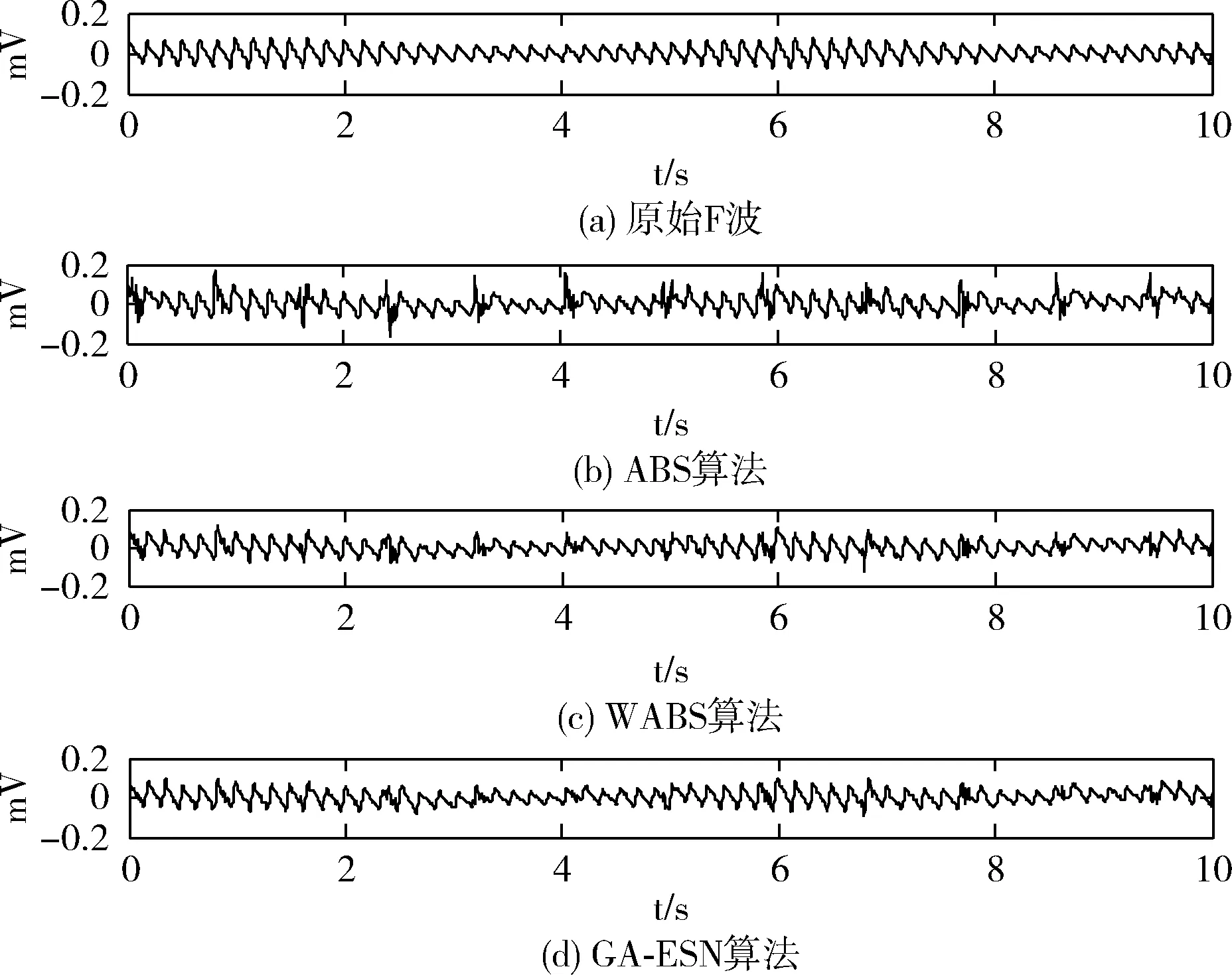
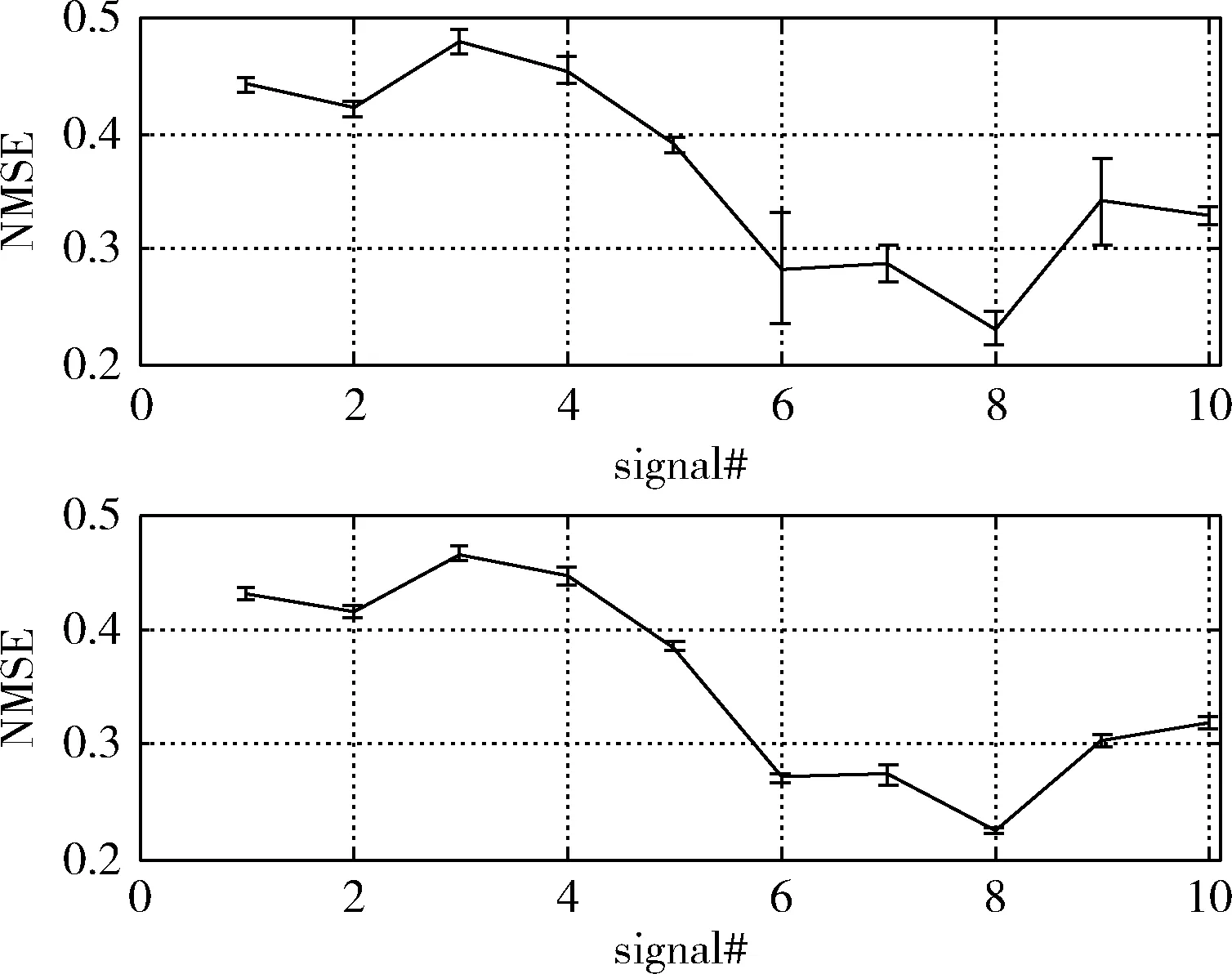
4.2 真实房颤信号F波的提取
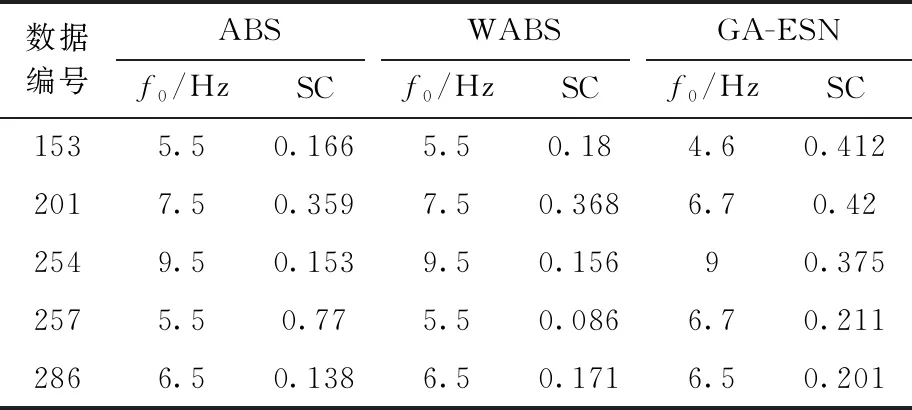

4.3 结果分析
5 结束语

