能量有效的无线传感器网络动态任务调度算法

朱晓娟，何勇男

(安徽理工大学 计算机科学与工程学院，安徽 淮南 232001)

0 引 言

近年来，国内外学者广泛研究了无线传感器网络动态任务调度问题[1-4]。文献[5]依据子任务预计完成时间及权重系数求出关键子任务，优先选择调度能力强、处理效率高的节点执行。文献[6]将粒子群算法的自适应与动态联盟的灵活应对能力进行整合，通过加权方式得到适应度值获得全局最优分配方案。文献[7]提出一种自适应调度器体系结构，可动态地延迟执行低优先级任务，以减少低电量时的能量消耗。文献[8]提出了一种使用线性规划的动态联合任务分配算法，获得了更均衡的任务分配策略。文献[9]先将任务分配到不同的集群以达到减少能源消耗的目的，再将任务由集群分配给合适的传感器节点以平衡网络的能量损耗。文献[10]给出了一种带迁移策略的记忆蚁群优化算法MIACO(memory-based immigrants ACO)，根据动态环境对任务进行迁移。文献[11]针对以上问题提出一种基于记忆的动态任务调度算法，它首先利用基于异或的动态环境生成器模拟了无线传感器网络中因节点失效产生的动态网络拓扑变化，再对模拟的动态环境进行实时感知，使算法能够自适应动态环境以降低能耗。但它在模拟环境的过程中，并没有考虑传感器节点的感测质量[12]，例如覆盖率[13]等问题，这与实际应用中的无线传感器网络节点有很大区别。

本文在文献[11]关于感知动态环境的基础上，对传感器节点的覆盖率、可调度性等做了一定的约束，并且对于节点的加入和离开对网络的影响进行了更为细致的探讨，可以有效节约网络的节点能量。同时，出于对网络负载均衡及能量最小化的考虑，将蚁群算法进行改进后应用于动态任务调度中，可以延长网络的生存周期。

1 动态任务调度模型

1.1 网络模型

在本文中，我们考虑如图1所示的无线传感器网络。节点与各种类型的传感器集成在一起，例如超声波传感器，光电传感器，红外传感器等，每个传感器负责其传感区域内相应目标的传感任务。通过不同符号标记的感测任务对目标实行分类，即图1中的▲，■，●，★。在任意时刻，传感器节点都可以精确地感测每一个目标。我们首先对节点的相关约束进行探讨。

图1 网络模型

1.1.1 覆盖率约束

文献[11]尽管可以快速感知环境变化，但却忽视节点对于目标的覆盖质量，任务无法调度至所有的节点上执行。传感器节点能够同时感测不同目标的多个任务。给定的感测任务通常涉及多个传感器以实现一定的感测质量，例如覆盖率就是一种通常采用的感测度量。设计节能传感器调度和管理策略是重要的，并保证所有任务的传感质量。

设S和T分别表示传感器集合和任务集合。对于任务t∈T， 其感测目标集由Gt表示，并且所需的覆盖率由dt表示。在不失一般性的情况下，我们假设传感器节点和感测目标在网络区域中随机分布。只有在传感器s的感知范围之内，任务t∈T的感测目标g∈Gt才能够被传感器s监测到。我们可以用vstg来表示这种情况

(1)

再定义一个二进制变量αst来表示传感器s是否调度任务t，如下所示

(2)

无线传感器网络中的传感质量需满足两点，一是目标t在s的感测范围内，即vstg=1； 二是感测任务t被调度时，传感器s∈S可以感知任务t∈T的目标g∈Gt。 用βstg表示传感器s是否能够感知任务t的目标g，有

βstg=αstvstg, ∀s∈S,t∈T,g∈Gt

(3)

对于被覆盖的感测对象，必须保留其最小感知率以确保感知精度。目标的感知率fstg首先由βstg确定，其中，ft为最小采样率

0≤fstg≤βstg·ft, ∀s∈S,t∈T,g∈Gt

(4)

这表示只有当传感器s能够感知任务t的目标g时，才能为fstg分配大于0的值。

多个传感器可能感测同一个目标。例如，如图1所示，黑色三角形中的任务1的目标可以由传感器A、B和C在它们的重叠覆盖范围内被感测。有效感知率不是简单地叠加这些传感器的感知率，因为对相同目标进行感知会被认定是重复行为应被忽略。则感知任务t的目标g的协同有效感知率为

(5)

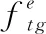
(6)

为了确保每个感测任务的感测质量，对于覆盖率δt有以下限制，其中Gt为感测目标的集合

(7)

1.1.2 可调度性约束

接下来进行可调度性约束的探讨。若当前任务均满足可调度性判定条件，则认为节点可调度。相反，若某个任务不能满足可调度性判定条件，则认为节点不可执行该任务。由于传感器节点可以具备多个感测目标，感测目标g∈Gt， ∀t∈T在传感器节点s∈S上需要一定的感知率fstg和持续时间ct。所有传感器节点必须满足以下限制，以确保多任务可调度性

(8)

1.2 传感器节点动态变化

在实际的无线传感器网络中，传感器节点由容量有限的电池供电，且通常无法充电，这会影响整个传感器网络的寿命,使得一些任务无法正常执行，因此，网络会重新部署节点。即在动态网络中，现有节点将因能量耗尽或者故障而离开，而新节点将会加入进网络中。

首先考虑在网络中部署新节点的情况。虽然让新节点保持睡眠状态并不会降低感测质量，但是会失去许多减少原有活动节点数量的机会。如图2所示，两个传感器节点A和B分别感测两个目标，当有新节点 C加入时，汇聚节点(sink)根据节点C的位置、传感质量、覆盖率等信息发现其感测范围内的潜在感测目标，当其感测范围能够覆盖图中两个目标时，我们可以停用节点A和B仅保持节点C处于活动状态。

图2 C节点可覆盖A、B两节点内的任务

然后考虑传感器节点离开网络的情况。如图3所示，当分配有感测任务的传感器A节点离开网络时，其邻居节点应能够发现这种事件并将其报告给汇聚节点(sink)，而任务1和3的目标在节点A离开之后变得未被覆盖，因此，需要激活节点B和C节点以确保覆盖要求。

图3 A节点离开时，需激活B、C节点

根据本节对于网络和节点的讨论，我们可以确定每个任务可调度节点集合，在下文中用调度算法将任务调度至相关节点处执行。

2 动态优化目标

在无线传感器网络中，动态环境会对任务调度产生一定的影响。因此，本文的动态优化目标不仅需要找到最优解，还应当在环境发生改变时及时调整调度方案。假设一个无线传感器网络,其应用程序按功能分为m个任务：M={Mj∶j=1,2,…,m}。 网络有n个传感器节点：N={Ni∶i=1,2,…,n}。 任务调度的目的是把m个任务合理调度至n个传感器节点，最优解为环境发生动态改变时，使所有任务完成的总能耗最低的分配方案。

2.1 任务完成能耗

无线传感器网络中，任务调度不仅需要满足应用对服务质量的要求，还要尽可能减少任务的总能耗，该总能耗是指各传感器节点完成任务的能耗之和。由于当前考虑的传感器网络不同节点的计算能力和通信带宽具有差异，使得任务调度到不同的传感器节点上执行需要的能耗也会不同。因此，需要根据每个传感器节点的计算能力及每个任务的大小来进行任务调度。本文采用的WSN能耗模型主要由通信和计算能耗两部分组成。

2.1.1 通信能耗

无线传感器网络大部分能耗由数据的发出和接收构成，本文中节点数据发送能耗和接收能耗分别用ET和ER表示。

数据发送能耗

ET(l,d)=l(Eε+Ea×d3)

(9)

数据接收能耗

ER(l)=lEε

(10)

其中，l为数据包大小，d为发送距离，Eε为发送或者接收每比特数据的能耗，Ea为每比特数据到每平方米的范围内发射放大器所消耗的能量。

2.1.2 计算能耗

Eproc=eproc×Tproc

(11)

其中，eproc为节点在单位时间内的耗能，Tproc为任务所占用的计算时间。

2.1.3 总能耗

综上，单个任务执行的能耗应为

Ecost=ET+ER+Eproc

(12)

则执行所有任务的总耗能为

(13)

除了对总能耗的考虑，无线传感器网络的寿命也是任务调度中的关键评估部分。为了延长网络寿命，我们应该平衡每个传感器在活动期间的能耗。我们可以基于熵理论[14]来测量传感器节点剩余能量的均匀性。

数据传输后传感器剩余能量的均匀性可表示如下

Hi=-∑p(Ei)logp(Ei)

(14)

其中，p(Ei) 是传感器节点i的剩余能量在所有节点剩余能量的比值，Hi是网络中残余能量熵的值。信息熵是从物理学范畴中引入的度量不确定方法的概念，是系统不确定性的有效度量。若不确定性越大，在式(14)中各节点占所有节点的剩余能量的比值p(Ei) 趋于相等，即Hi越高，网络负载越均衡，网络寿命越长。

2.2 动态优化目标

本文算法的动态优化目标和约束设定为

(15)

3 传感器动态任务调度算法

在确定动态环境下每个任务的可调度节点的集合之后，便可以将任务进行调度。原始蚁群算法常被用于搜索和优化路径问题，在本文中，我们将任务调度过程中的一次任务分配当作原始蚁群算法的一条路径，同时考虑到WSN中网络动态环境及原始蚁群算法易陷入局部最优等特性，需要对算法做进一步的改进。

3.1 概率转移函数

蚂蚁为任务选择执行节点时，要通过如下概率转移函数进行选择，其中，i为任务执行节点，Γ为当前任务M允许选择的节点集合

(16)

原始蚁群算法的启发函数是由距离的倒数来表示，但在任务调度中发挥作用较小，因此引用最大信息熵原理[14]对启发因子进行改进：

n为节点数，Ei(t+1) 为节点i的剩余能量，有

(17)

再用信息熵表示下一时刻网络中节点能量分布情况

(18)

ηi(t)=H(t+1)

(19)

要使下次循环网络内能量均衡，需使H(t+1) 最大，各节点能量值近似于均匀分布。启发因子的值越大，被选中的概率越大。

3.2 信息素扩散

原始蚁群算法由于正反馈作用，易使某些节点信息素越积越多，导致节点负载过重，为避免这种情况，每只蚂蚁完成一次任务分配后，都要对信息素进行扩散，公式如下

τi(t+1)=(1-ρ)·τi(t)+Δτi(t)

(20)

其中，ρ是信息挥发因子，表示信息素的挥发程度， 1-ρ表示信息残留程度，ρ∈(0,1)。

(1)当一只蚂蚁完成任务分配后，会得出一种分配方案，需要进行局部信息素的更新

(21)

其中，Q1为局部信息素强度，E(A)为第i只蚂蚁在第nc次迭代中的分配方案所产生的任务调度能耗。

(2)当前代所有蚂蚁完成任务分配后，需要对所有的分配方案进行比较，得出最优值，更新信息素。其中，仅对最优分配方案进行全局信息素的更新，而其它分配方案的信息素就会逐渐的衰减，对算法的搜索具有一定的方向性，有利于缩小搜索范围

(22)

其中，Q为全局信息素强度， min(E(A)) 为第nc次迭代中最优分配方案所得出的能量消耗。

4 算法流程

步骤1 初始化参数，包括算法的迭代次数nc，蚂蚁的数量k，任务的数量m，信息素挥发率参数ρ，概率转移函数中两个权重参数α和β。

步骤2 sink节点根据当前环境所产生的约束，确定每一个新到达任务的可调度节点集合，记为ΓM。初始化最优任务调度方案。

步骤3 启动改进后的蚁群算法，每只蚂蚁按照概率转移函数(16)为任务分配合适的节点，得出解的值即为分配方案。

步骤4 当一只蚂蚁完成任务分配之后，要按照式(21)进行信息素局部更新。

步骤5 判断当前代蚂蚁是否循环完毕，若否则重复步骤3和步骤4。若全部蚂蚁循环完毕，则通过式(22)对信息素进行全局更新。

步骤6 判断迭代是否终止，若否增加迭代次数，检测当前环境是否发生改变，若发生改变，则输出最优任务调度方案，并返回步骤2；若环境没有发生改变，则返回步骤3。若达到最大迭代次数，则算法结束。

5 仿真实验及分析

5.1 实验环境设置

本文中仿真程序是用Matlab 2017软件编译运行，在100 m2*100 m2的监测区域随机部署不同数量的异构传感器节点，数目为50个，节点初始能量相同，记为2 J。式(9)、式(10)的参数设置为：Eε=50 Nj/b，Ea=0.1 nJ/b/m2。 在改进的蚁群调度算法中，迭代次数设为300次，环境每隔50次变化一次，节点变化(加入和离开)的概率为[0，0.05]。ρ为0.4，α为1.5，β为2。

5.2 实验与分析

本节采用文献[10]提到的带有迁移策略的蚁群算法(MIACO)以及原始蚁群优化算法(ACO)与本文提出的算法进行对比。

由图4可以看出，本文提出的算法可以对环境的变化进行感知，能以较快的速度得到最优解，其收敛速度、最优分配方案得出的任务能耗均优于其它两种算法。

图4 环境每隔100代变化一次的任务能耗

图5为算法迭代到300次时得出的分配方案中任务总执行时间。在传感器节点的数量不变情况下，随着任务数量的增加，分配给每个传感器节点的任务量也增加，因此任务分配的总执行时间也会增加。但需要注意的是，任务分配的总执行时间并不是全部任务分配时间的总和，如式(24)所示，应当与任务分配执行时间最长的传感器节点相同。用Tij表示任务Mj在节点Ni上的执行时间，则分配给第i个传感器节点的所有任务的执行时间可以表示为

(23)

任务分配总执行时间可以被表示为

T=max(ett(i))

(24)

从图5中的情况可以看出，带有迁移策略的蚁群算法执行任务所耗费的时间最多，这是因为任务迁移消耗了大量时间，原始蚁群优化算法倾向于将任务调度至最优点执行，从而导致大量任务拥挤于某些特定节点，负载不均衡，排队将耗费大量时间。而本文提出的任务调度算法缓解了蚁群算法易陷入局部最优的问题，并根据网络的整体负载情况，将任务调度至剩余能量充沛的节点执行。

图5 任务的执行时间

图6是网络中节点为100的情况下，完成300次迭代后，各节点能耗与网络中平均能耗的差值同网络中平均能耗的比值。如式(25)所示，ei为第i号节点的能耗，eave为网络中节点的平均能耗。比值越接近0，代表网络中的能量均衡状况越好。本文提出的任务调度算法由于在启发函数中加入了剩余能量的信息熵值，各节点的能耗基本相同，不会对网络中某些节点造成较大负载影响。这种考虑网络负载因素的算法可以延长节点死亡时间，进而提升网络的整体寿命

(25)

图6 能量负载均衡状况

6 结束语

本文针对现有的任务调度算法的局限性，提出了能量最小化的动态任务调度算法。通过对动态环境变化进行感知，包括了节点的加入和退出，同时从覆盖率、可调度性对可调度节点进行了约束。再根据改进蚁群算法将任务调度至剩余能量较为充沛的节点执行。通过仿真实验可以得出，本文提出的算法可有效缩短任务的执行时间和减少能耗，对网络负载起到了很好的平衡作用，延长网络寿命。