融合UWB测距信息的室外高精度定位算法
周爱国 ,杨思静 ,沈 勇 ,王嘉立
0 引言
智能驾驶汽车需要高精度的稳定定位信息,以满足各场景的应用需求,如碰撞预警、并线等[1-2]。目前的智能驾驶汽车定位系统高度依赖于差分定位的全球卫星导航系统(global navigation satellite system,GNSS),不仅价格昂贵而且在城市环境中极易因信号遮挡而引起误差,造成车载定位系统在城市环境下定位误差的增大和稳定性的降低[3]。惯性导航系统(inertial navigation system,INS)利用惯性敏感元件来推算载体的位置、速度和姿态,可实现自主定位,但其误差会随时间累积以致定位精度随时间发散。作为GNSS定位技术的1种,单点定位模式的全球定位系统(global positioning system,GPS)定位精度较低,但能够提供全方位、全天候的定位信息且价格较低。基于扩展卡尔曼滤波的GPS/INS组合定位算法结合GPS和INS的误差特性保证定位信号的稳定输出,但其定位误差难以达到分米级[4]。
地图匹配是1种软件纠错技术,将车辆行驶轨迹与高精度电子地图进行匹配,从而确定车辆在地图中的位置[5]。但现有地图匹配技术存在鲁棒性差、可用路标有限等缺点,且大部分地图匹配技术主要修正沿车道方向的纵向定位误差,而对相对于车道的横向定位研究还较少[6]。实际上,横向定位精度对车辆的行驶安全起着至关重要的作用,如超车和并道过程中的 2车横向间距一般不超过1 m。考虑到车辆沿车道行驶时,行驶轨迹基本平行于车道线,且与车道线距离保持稳定,因此可以通过车辆的历史轨迹推算出车辆的未来行驶轨迹,即航迹。本文将提出1种推算航迹的方法,并融合航迹对车辆进行横向定位。
在室内定位领域,超宽带(ultra wideband,UWB)技术作为 1种无线电技术,将信号传输时间转换为距离信息,可以实现厘米级的定位精度,但主流的基于到达时间(time of arrival,TOA)和基于达到时间差(time difference of arrival,TDOA)的定位技术都至少需要设置 3个基站,硬件成本较高且系统复杂[7]。在立交桥、树荫遮挡等复杂城市道路环境下,GNSS定位精度严重下降,本文将利用 UWB技术辅助 GPS/INS组合定位系统,既降低成本又实现高精度的室外定位。
综上所述,本文在高精度车道线数据库和低精度GPS/INS组合定位的基础上提出1种融合UWB测距信息的室外高精度定位算法。以 GPS/INS组合定位信号作为稳定原始输出,针对沿车道行驶和路口转弯 2种情况分别提出单基站航迹匹配和扩展卡尔曼滤波(extended Kalman filter,EKF)组合定位算法。
1 定位算法方案与框架
UWB是1种无载波通信技术,利用微秒至纳秒级的非正弦波窄脉冲传输数据,可达到厘米级的测距精度,并且还具有处理增益高、输出功率低、抗干扰能力强、传输距离远等特点,因此可将其应用于室外定位中。融合UWB测距信息的室外高精度定位算法方案如图1所示。
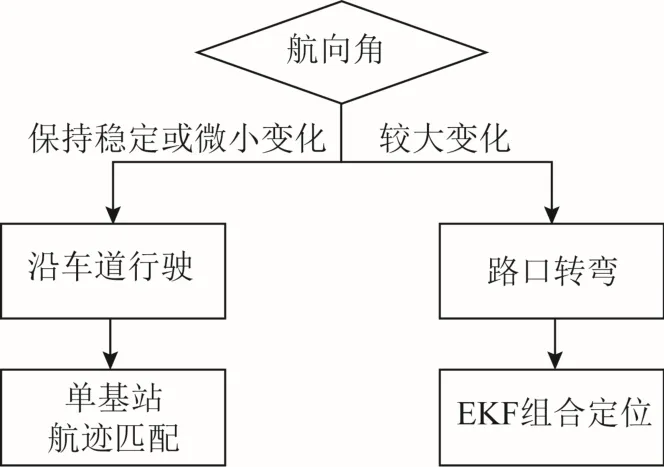
图1 定位技术方案
为了保证稳定输出,将 GPS/INS组合定位信号作为原始输出,其中包括位置、速度和航向角。因为车辆在路口转弯时不存在起引导作用的车道线,因此其定位方案与沿车道行驶时有所不同。实车实验中的航向角变化率如图2所示。
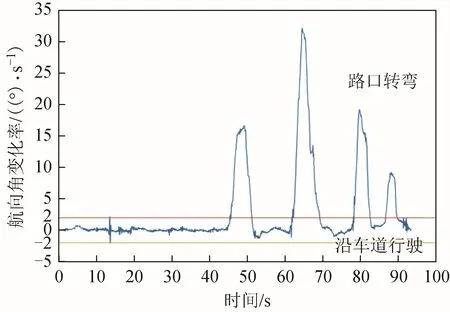
图2 航向角变化率
由实验结果可知,当车辆沿车道行驶时,大部分行驶时间内航向角变化率稳定在2(°)/s以内,因此可将其作为判断车辆行驶状态的基准。当航向角保持稳定或微小变化时,可判定车辆处于沿车道行驶阶段,通过车辆行驶历史轨迹计算车辆在车道上的横向偏移量,根据车道线数据库确定车辆行驶航迹,最后结合UWB测距信息进行单基站航迹匹配[8];当航向角发生较大变化时,可判定车辆处于路口转弯阶段,由于UWB测距信息与车辆的位置存在非线性关系,因此通过EKF结合原始定位数据和UWB测距信息进行组合定位[9]。
另外,为了保证UWB的测距精度,应将UWB基站布置在相对空旷的环境下,抑制其非视距误差。
2 单基站航迹匹配
本文根据UWB的高精度测距特性提出了1种应用于室外定位的单基站航迹匹配算法,主要包括融合横向位移的航迹推算和融合纵向位移的圆交点求解。
2.1 航迹推算
由驾驶员驾驶习惯可知,沿车道行驶时其行驶轨迹平行于车道线,且与车道线的横向距离保持稳定,因此本算法设计在每个路口放置1个UWB基站,同时在车辆顶部安装UWB移动站,通过计算车辆在进入车道后稳定行驶 1段距离的平均横向距离推算出未来行驶的航迹。
为了提高航迹推算的简便性和精确性,根据行驶策略将处于交叉路口的车辆分为 2种情况:直行(如路径1)和路口转弯(如路径2),如图3所示。由 UWB基站的经纬度坐标与车道线数据库坐标点集计算UWB基站与车道线之间的距离 d2。
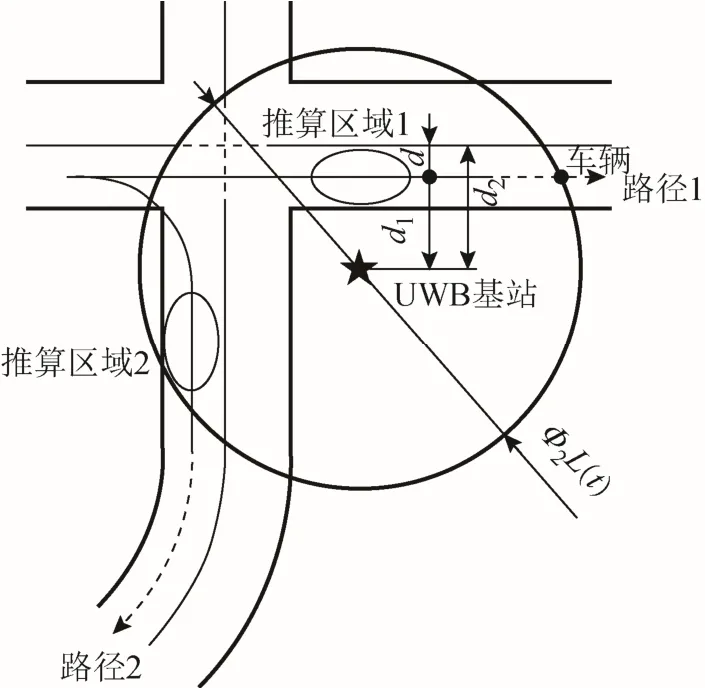
图3 路口行驶策略
2.1.1 直行时的航迹推算
以图3中路径1为例,车辆直行通过路口时,车辆进入推算区域 1后稳定行驶,其 UWB基站与车辆 UWB移动站之间的距离特征曲线如图 4所示。可取距离特征曲线的最低点作为行驶航迹与 UWB基站之间的距离 d1,则行驶航迹与车道中心线之间的距离为d=d2-d1(设定车辆在车道中心线以右时d为正值)。最后将车道中心线向右横向平移距离d,即可得到行驶航迹,即路径1(虚线部分)。
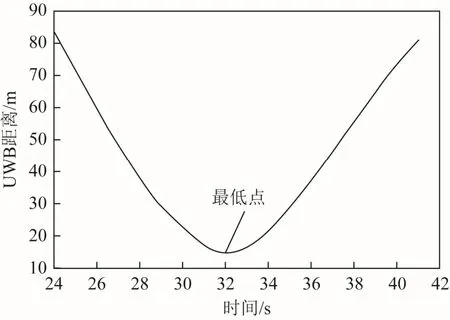
图4 直行时距离特征曲线
2.1.2 路口转弯后的航迹推算
以图3中路径2为例,车辆转弯通过路口后,车辆进入推算区域2后稳定行驶。此时,UWB基站、行驶航迹和车辆之间的几何关系可以简化为图5所示几何关系。
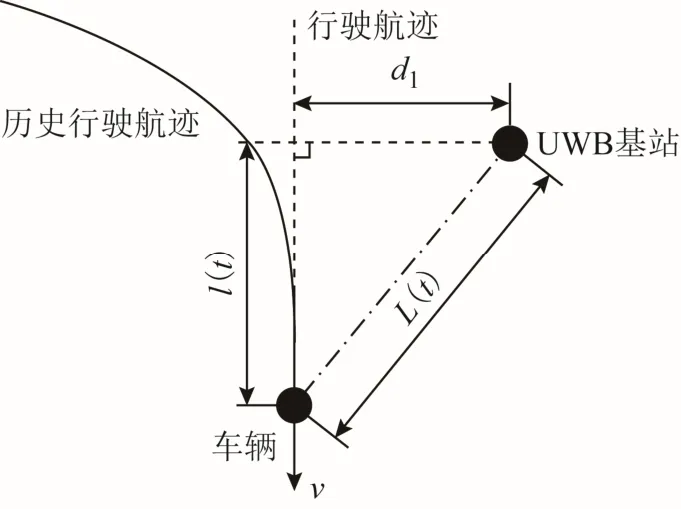
图5 几何关系示意图
根据勾股定理可得

式中:L(t)为t时刻UWB基站与车辆的距离;d1为UWB基站与行驶航迹的距离;l(t)为t时刻车辆与UWB基站在行驶航迹上的投影点的距离;t为行驶时间。
由式(2)可得UWB基站与行驶航迹的距离为
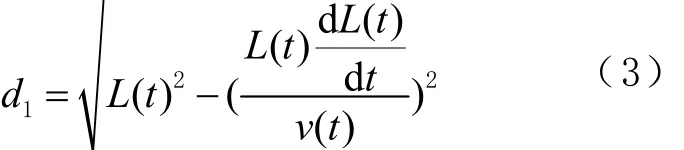
根据 d1可求得行驶航迹与车道中心线之间的距离为d=d2-d1。最后将车道中心线向右横向平移距离 d,即可得到行驶航迹,即路径 2(虚线部分)。
2.2 圆交点求解
车辆确定行驶航迹后,即可通过圆交点求解确定其纵向位移。如图2所示,在t时刻,以UWB基站坐标(xUWB,yUWB)为圆点,UWB的测距特征L(t)为半径作圆,与行驶航迹的交点即为车辆位置。联立方程为
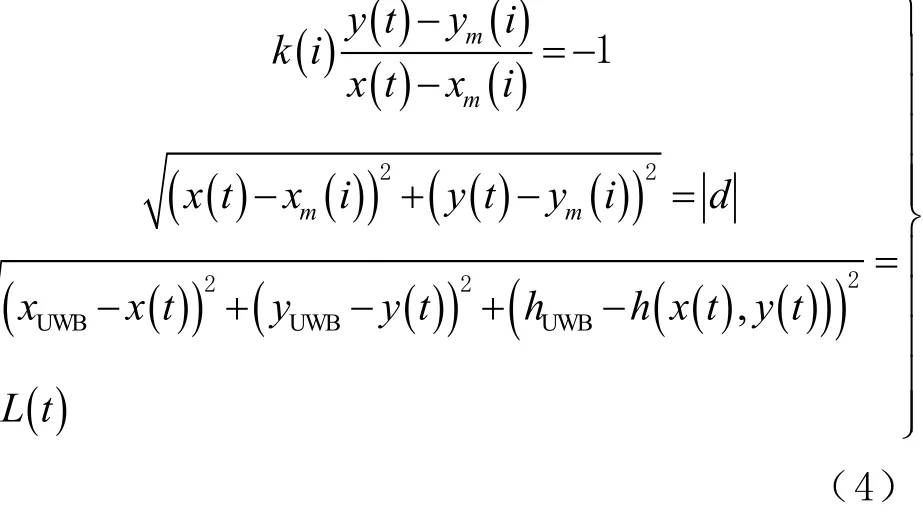
式中:(x(t),y(t))为t时刻车辆在行驶航迹上的路点坐标,即车辆定位结果;{(xm(i),ym(i))}为高精度车道线数据库坐标点集(i为点集序列),由高精度定位模块测得;k(i)为车道线在第 i个车道线点处的(xUWB,yUWB)为 UWB基站的路点坐标;hUWB为UWB基站的安装高度;h(x(t)、y(t))为t时刻UWB移动站在路点(x(t)、y(t))的安装高度分布函数,考虑到城市环境下大部分道路为平整路段,即h(x(t),y(t))≈常数 h',h'的值可通过实验获得。当车辆通过桥梁或立交桥路段时,道路高程在短时间内发生变化,因此可利用 INS解算车辆高程上的变化 h",此时 h(x(t),y(t))≈h'+ h"。
通常情况下,上述方法将求得多个圆交点。根据 d的正负性判断车辆在车道中心线的左侧还是右侧。在匹配的初始化阶段,将靠近 GPS/INS定位坐标的交点作为匹配起始点;在后续的匹配过程中,则采用与上1次匹配位置最近的交点。
3 EKF组合定位算法
当车辆路口转弯时,不存在起引导作用的车道线,这就需要利用GPS/INS组合定位原始输出和 UWB的测距信息进行数据融合,获得精确的定位信息。考虑到UWB的测距信息 L (k)=(为了表述方便,和车辆位置(x(t),y(t))成非线性关系,且其相应的雅可比矩阵较易求得,因此采用计算量较小的EKF滤波进行参数估计。EKF滤波算法建立在线性卡尔曼滤波的基础上,其核心思想为:对一般的非线性系统,融合滤波值X ˆ(k)将非线性函数 f(*)和 p(*)展开成泰勒级数并略去 2阶及以上项,得到 1个近似的线性化模型,然后利用线性卡尔曼滤波完成对目标的滤波估计[10]。
根据车辆运动学分析,取状态量 X(k)=[x(k),ẋ(k),y(k),ẏ(k)]T,采用 CV 模型,则系统状态方程为
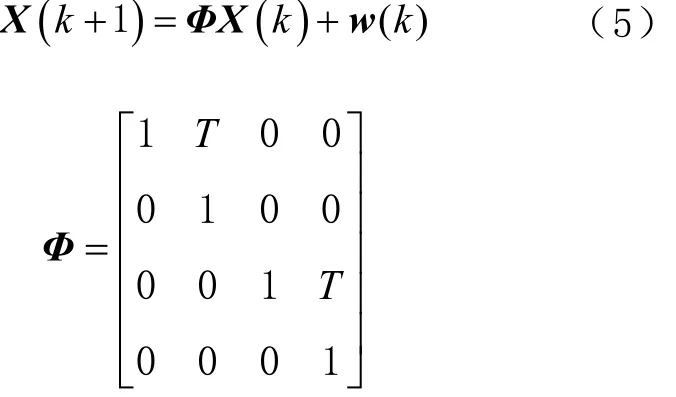
式中:x(k)和y(k)为k时刻车辆在东向和北向的位置;ẋ (k)和 ẏ (k)为 k时刻车辆在东向和北向的速度;T为UWB采样周期;w(k)为k时刻的系统噪声,是均值为零的高斯白噪声,其对应的协方差矩阵为Q,其值可由实验确定。
以 UWB测距信息 L(k)、车辆的位置(x(t),y(t))和速度(ẋ (t),ẏ (t))作为观测量,则观测方程为
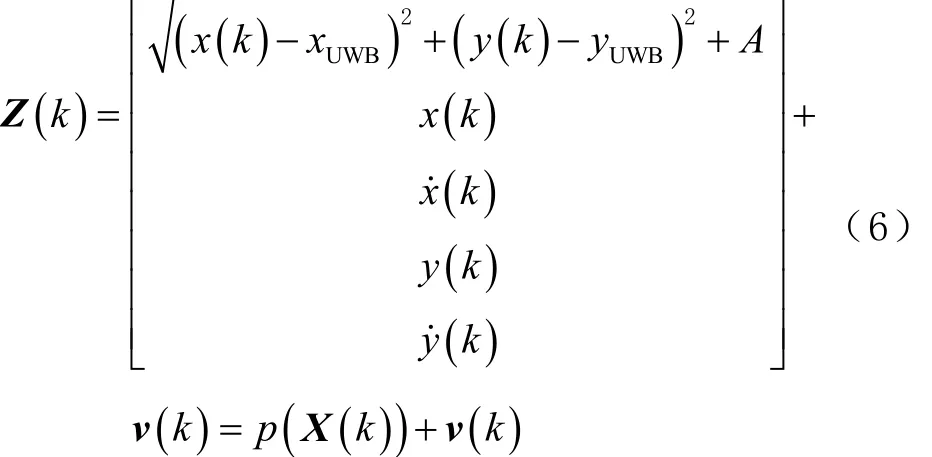
式中,v(k)=[vL(k),vx(k),vẋ(k),vy(k),vẏ(k)]T为 k 时刻的测量噪声,是均值为零的高斯白噪声。其中vL(k)为 UWB 的测距误差,vx(k)、vẋ(k)、vy(k)和 vẏ(k)为GPS/INS组合定位系统的测量误差。v(k)对应的协方差矩阵为R,其值可由实验确定。
由式(6)可知,系统观测方程为非线性方程,根据EKF的泰勒(Taylor)级数展开方法,求得对应的雅可比矩阵为

式中I4为4阶单位矩阵。
最终可将观测矩阵简化为线性的形式,即
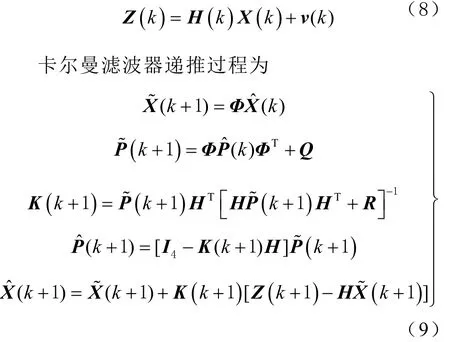
式中:X(k) 和X (k)为 k时刻状态量的滤波值和预测值; Pˆ(k)和P(k~)为 k时刻误差协方差矩阵的滤波值和预测值;K(k)为 k时刻滤波增益矩阵。
4 实验与结果分析
为了验证本文提出的定位算法的合理性及其高定位精度,在4个路口各安装1个UWB基站且安装高度与车载 UWB移动站一致,围绕同济大学机械学院进行实车实验。其中,GPS接收机为 u-blox LEA-6H,MEMS传感器为 MPU6050,UWB模块为DW1000。实验时以RT3000高精度定位模块的定位数据作为车辆的参考定位轨迹,进而比较融合本文定位算法的定位轨迹与标定轨迹的偏差。
图6和图7分别为GPS/INS组合定位算法和本文定位算法的横向和纵向误差曲线。GPS/INS组合定位算法的横向误差和纵向误差平均值分别为1.07和 4.73 m。而本文定位算法大部分横向误差和纵向误差均在1 m以内,且平均误差分别为0.24和0.4 m,满足智能驾驶中的分米级高精度定位要求。但在弯道处有较大的偏差,这是因为在沿车道行驶时,车辆的定位精度高度依赖于UWB的厘米级测距精度和高精度车道线数据库,所以最终的精度也能保证在40 cm以下。而在邻近弯道处车辆的定位精度由低精度的 GPS/INS组合定位信号和UWB模块共同决定,因此相对于沿车道行驶的定位精度较低。
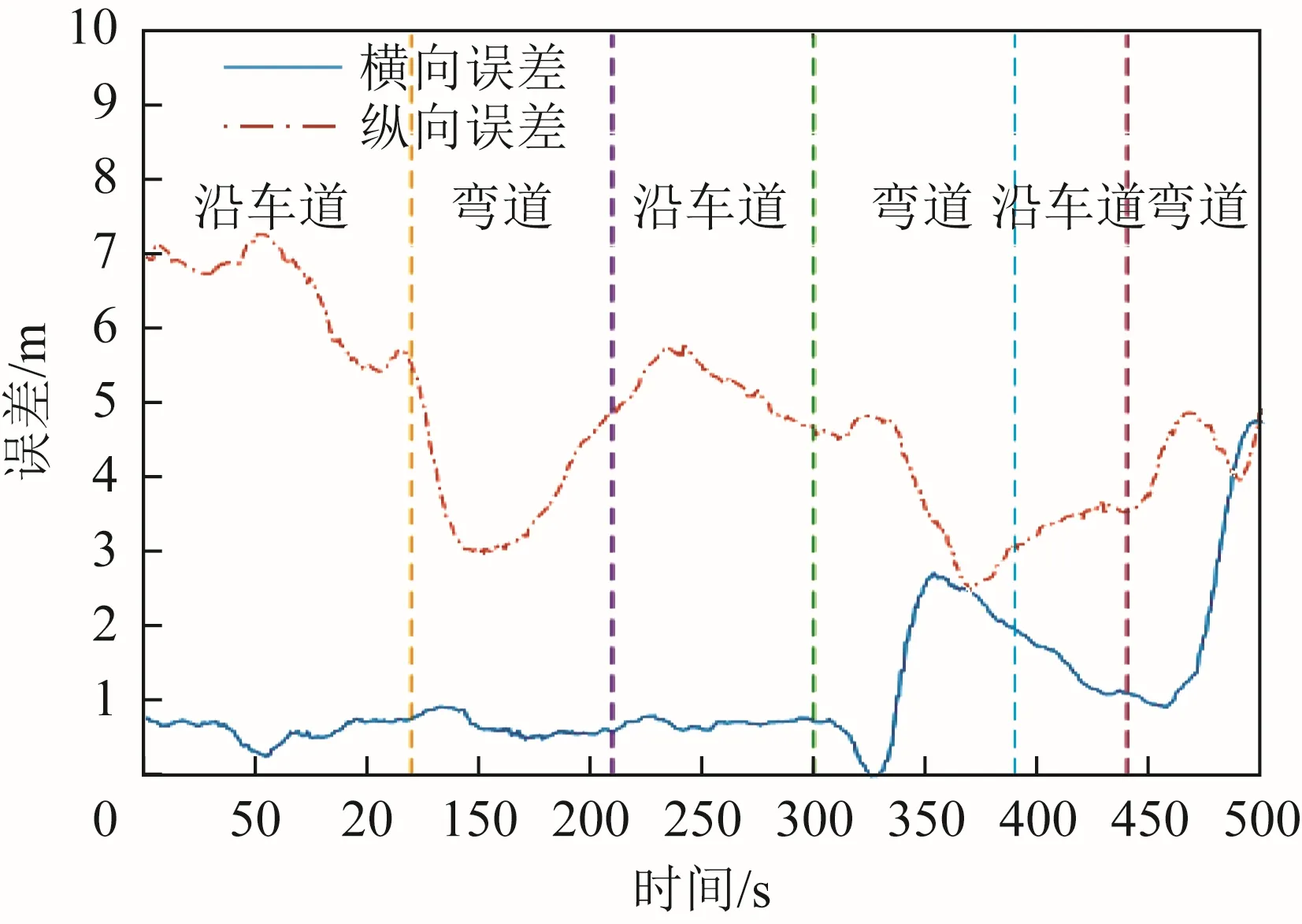
图6 GPS/INS组合定位算法曲线
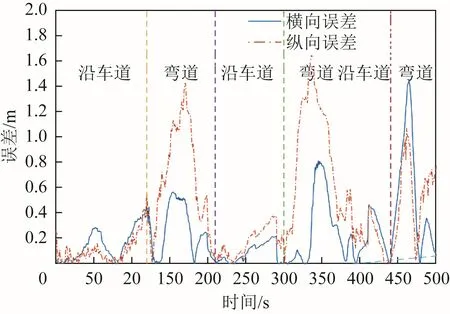
图7 本文定位算法误差曲线
实车实验轨迹如图8所示,其局部放大图如图 9所示。GPS/INS组合定位算法与标定轨迹存在较大偏差,融合UWB测距信息的室外高精度定位轨迹与轨迹基本重合,证明了本文定位算法的优越性和可靠性。
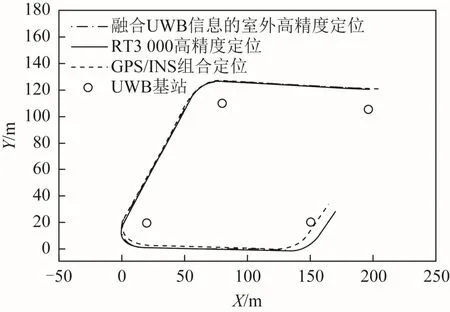
图8 实车实验轨迹结果
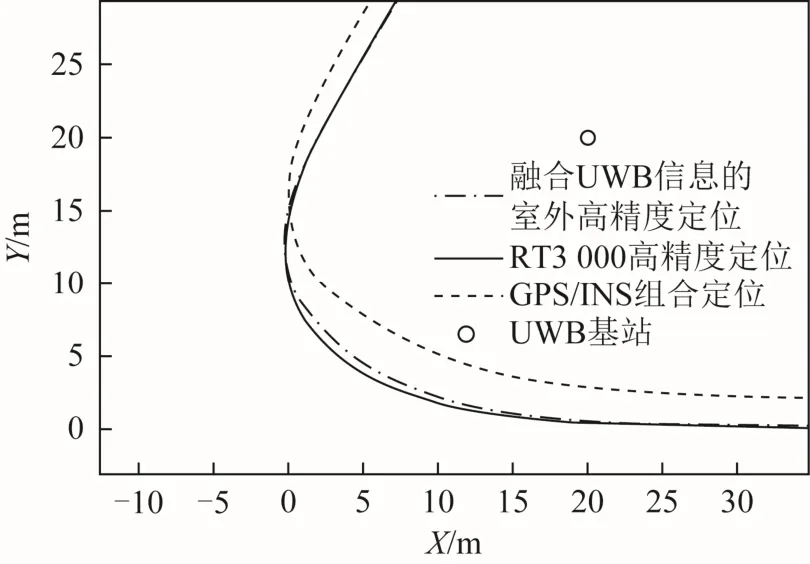
图9 实车实验轨迹结果局部放大图
5 结束语
本文在 GPS/INS组合定位和 UWB技术的基础上提出了 1种融合 UWB测距信息的室外高精度定位算法。在沿车道线行驶情况下,综合驾驶员的驾驶习惯和 UWB的高精度测距特性提出了单基站航迹匹配;在弯道情况下,利用 EKF融合GPS/INS组合定位原始输出和UWB的测距信息。实车实验结果表明,该算法准确可靠,能广泛应用于智能驾驶的导航定位中。

