BDS卫星精密钟差性能综合评定
王 威 ,王宇谱 ,王 彬 ,赵华凯
0 引言
星载原子钟是卫星有效载荷的一部分,是卫星导航系统的星上时间参考[1-2]。由于全球卫星导航系统(global navigation satellite system,GNSS)是以时间测量为基础的系统[3],因此获得高精度的卫星钟差数据越发成为提高 GNSS定位导航性能的关键,同时也是实现高精度星间测距,星地测距和时差监测的基础。其中,对于卫星钟差数据的质量分析将有助于深入认识钟差数据特性,有助于改进钟差拟合预报策略、提升钟差产品性能、优化钟差时频传递模型,进而提高导航定位授时的效果。正因如此,吸引了不少国内外学者的广泛关注[4-9]。文献[4-5]利用国际 GNSS服务中心(International GNSS Service,IGS)提供的精密钟差数据,对全球定位系统(global positioning system,GPS)广播星历卫星钟差进行了精度评定;文献[6]利用频谱分析手段,对GPS精密星历中各卫星的钟差精度进行了分析,发现大部分的卫星钟差精度能达到IGS的标称值,但仍有部分卫星钟差的精度低于其标称值;文献[7]对比分析IGS提供的300和30 s间隔采样的GPS精密卫星钟差的变化规律;文献[8]分析了IGS实时产品的质量;文献[9]利用多 GNSS实验项目(multi-GNSS experiment,MGEX)数据,对比了分析中心间GPS精密卫星钟差数据的精度。这些研究成果虽然提供了精密钟差数据质量评估的方法与思路,但是均围绕 GPS系统精密卫星钟差展开的,并未给出有关BDS的精密星钟数据质量分析。
随着北斗卫星导航系统(BeiDou navigation satellite system,BDS)进入全球组网阶段[10],开展BDS卫星钟差精度分析与评定的相关研究,将对提升系统服务能力有着重要意义。目前,BDS体制精密钟差数据可以通过双向时间比对(two-way time transfer,TWTT)和精密定轨与时间同步(orbit determination and time synchronization,ODTS)获得,由于 TWTT体制可以消去电离层延迟、卫星轨道误差等诸多公共误差,因此该方法得到的卫星钟差具有较高的精度。但是,TWTT卫星钟差对于普通用户一般不易获取。ODTS体制将钟差和轨道一并解算,是 1种广泛采用的卫星钟差确定手段,相关的算法和研究相对较多。当前,IGS的欧洲 定 轨 中 心 ( Center for Orbit Determination in Europe,CODE)、德国地学研究中心(Deutsches GeoForschungsZentrum,GFZ)及武汉大学卫星导航定位技术研究中心(GNSS Research Center of Wuhan University,WHU)3 家分析中心可以提供BDS精密卫星钟差数据,不少学者利用MGEX的精密星钟产品开展了 BDS卫星钟差数据质量分析与评估工作[11-13]。文献[11]评估了WHU的BDS 精密钟差精度,发现多星定轨条件下钟差数据存在天跳变的现象。然而,不同分析中心估计的卫星钟差结果一般由联合定轨解算得到,不可避免地会受到定轨残余误差的影响。同时,即使是同一卫星各分析中心估计的钟差结果也会存在差异,其相对于TWTT卫星钟差也会存在偏差。在分析比较不同分析中心提供钟差产品时,文献[12]使用 IGS的事后精密钟差产品作为参考值进行评估,仍将 1部分轨道误差引入到参考钟差值中。文献[13]用TWTT结果作为参考与 WHU的精密星钟产品进行了比对,但并没有给出与CODE、GFZ星钟产品的评估结果。
基于此,本文充分利用 TWTT钟差结果不受轨道系统误差影响的优点以及BDS播发的卫星钟参数是基于 TWTT钟差结果计算产生的特点,以TWTT的钟差结果作为参考值,设计了 1种综合质量评定方法,从数据缺失率、内符合精度、外符合精度和时域频率稳定性的角度分析CODE、GFZ和WHU的精密钟差产品的质量及其相关特性。
1 计算方法
1.1 星地双向伪距时间比对计算流程
星地双向伪距时间比对法采用“互发互收”的工作模式,其基本原理可以概括为:地面站A在地面时间系统 T0A时刻向卫星发送测距信号,该信号被卫星接收设备于卫星上的钟面时 Ts时刻接收,并将观测数据发送给地面站。与此同时, T0S时刻卫星发射测距信号,并在地面钟面时刻 TA被地面站接收,此时星上接收设备和地面接收设备测得的上下行伪距[14]分别为
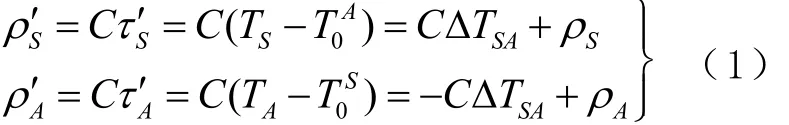
式中:C为光速;ΔTSA为卫星钟和地面钟之差;ρS′为星上接收设备测得的L波段上行伪距;ρS是TS时刻卫星至地面站的距离;ρ′A为地面接收设备测得的L波段下行伪距;ρA是TA时刻卫星至地面站的距离。式(1)中上下2式相减可得
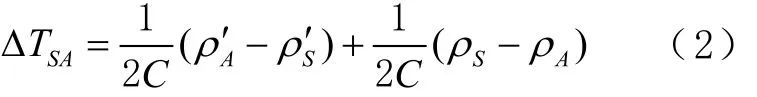
求得的SATΔ即为卫星钟和地面钟之差。对于BDS而言,此时的地面钟时间实际上是北斗时(BDS time,BDT),而 BDS 卫星钟与 BDT 之差,也就是BDS卫星钟差。
1.2 精密定轨和时间同步
ODTS利用 GNSS观测数据解算导航卫星的精密轨道和钟差,通常使用消电离层组合观测量,其相位与伪距观测量的误差方程可表示为
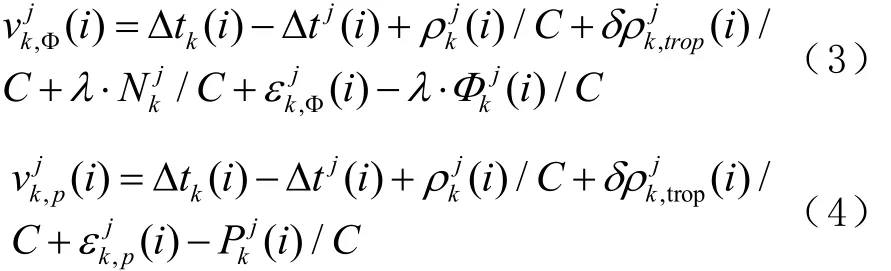
式中:j为卫星号;k为测站号;i为相应的观测历元;Δtk(i)表示接收机钟差;为对流层延迟影响; Δ tj(i)为卫星钟差;为多路径、观测噪声等未模型化的误差影响;为相应卫星、测站和历元的组合观测量;λ为相应的波长;为对应的观测误差;ρkj为信号发射时刻的卫星位置到接收机位置之间的几何距离[15]。
需要注意的是 GNSS观测值是站星之间的相对延迟,基于上面2个公式求解钟差参数时,法方程是奇异的,故须引入1个基准钟;在此基础上,再确定其他接收机与卫星的相对钟差;最后相对钟差值加上基准钟差值便可得到绝对卫星钟差值。在解算上面2个方程式时,主要有2种方法:①首先使用双差数据消去钟差,解算出卫星轨道等参数,然后将解算出的轨道固定再采用非差模式估计卫星钟差;②利用非差数据处理模式将轨道和钟差一起估计。这2种方法各有特点,合理使用均能取得较好的参数估计效果。
1.3 TWTT与ODTS 2种技术的区别
TWTT与ODTS技术提供的卫星钟差都是分析GNSS卫星钟的重要数据来源。区别于其他卫星导航系统,BDS采用 TWTT体制进行卫星系统时间与地面系统时间的同步[13]。通过对同一历元的双向伪距观测数据求差解算,得到精密卫星钟差。这种机制一方面可消除一部分公共误差,如对流层延迟、卫星轨道误差和地面测站坐标误差等,保证卫星钟差较好的一致性。同时也具有明显的技术复杂性,如精确测定测站和卫星的发射与接收延迟。
而 ODTS是 1种单向的定时技术,其算法不论是利用非差数据,将卫星轨道与卫星钟差一并进行解算,还是联合使用双差与非差数据进行轨道和钟差的估计[16],都不可避免地将轨道误差引入到卫星钟差,导致精密钟差结果呈现与轨道周期相关的误差特性[13]。同时,ODTS钟差通常是由3 d定轨弧段求解得到的中间天的钟差结果,受每个定轨弧段基准时间变化的影响,ODTS钟差可能会存在跨天的钟差跳变现象。
另外,由于TWTT钟差是利用伪距观测数据进行解算求得的,其观测结果会受伪距观测噪声的影响。而 ODTS使用载波数据或利用载波平滑伪距,得到的钟差在观测噪声上应该会明显区别于TWTT的结果。
1.4 质量评定方案
为定量分析2种技术手段获取的BDS卫星钟差质量情况,同时对比 IGS不同分析中心提供的精密钟差数据质量。本文设计了如下的质量评定流程方案:
先将获得到的 TWTT卫星钟差原始相位数据与3个分析中心的原始相位数据进行时标对齐,统计数据的缺失情况,作为数据连续性指标。再将卫星钟差相位数据转换为频率数据,并利用参数n=5的中位数法(MAD)进行粗差剔除。具体算法为
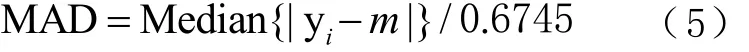
并对数据进行二次多项式拟合,统计各颗卫星单天拟合残差,作为内符合精度指标。
最后利用频率数据进行重叠哈达玛方差的计算,作为时域频率稳定度指标。具体算法如下:
设有一采样间隔为τ0的相对频率偏差数据序列{ yn,n = 1,2,… ,M },M为数据总个数。对于频率数据,其定义为

2 计算与分析
2.1 使用数据的情况
用于分析的数据起止时间为2018年2月1日至2018年4月30日,下载对应时间的com*.clk、gbm*.clk 以及 wum*.clk(数据下载网址: ftp: //cddis.gsfc. nasa. gov/pub/gps/products/mgex/)数据的采样间隔为300 s的精密钟差数据。TWTT数据,类似于文献[13,17-18]具有很高的比对精度和较好的一致性,因此使用同一时间的 TWTT数据作为参考值,数据采样间隔同为300 s。由于分析中心的数据时标基准为 GPS 时(GPS time,GPST),而TWTT数据时标基准为BDT,②者之间存在差异;因此,须将分析中心的时标进行转换,使之与TWTT的数据时标一致。再使用中位数法对数据进行筛选和预处理,得到剔除异常值的精密钟差数据。
2.2 钟差数据精度分析
2.2.1 数据的连续性分析指标
分别对CODE、GFZ、WHU和TWTT的BDS卫星钟差数据进行连续性评估,结果如表 1所示。
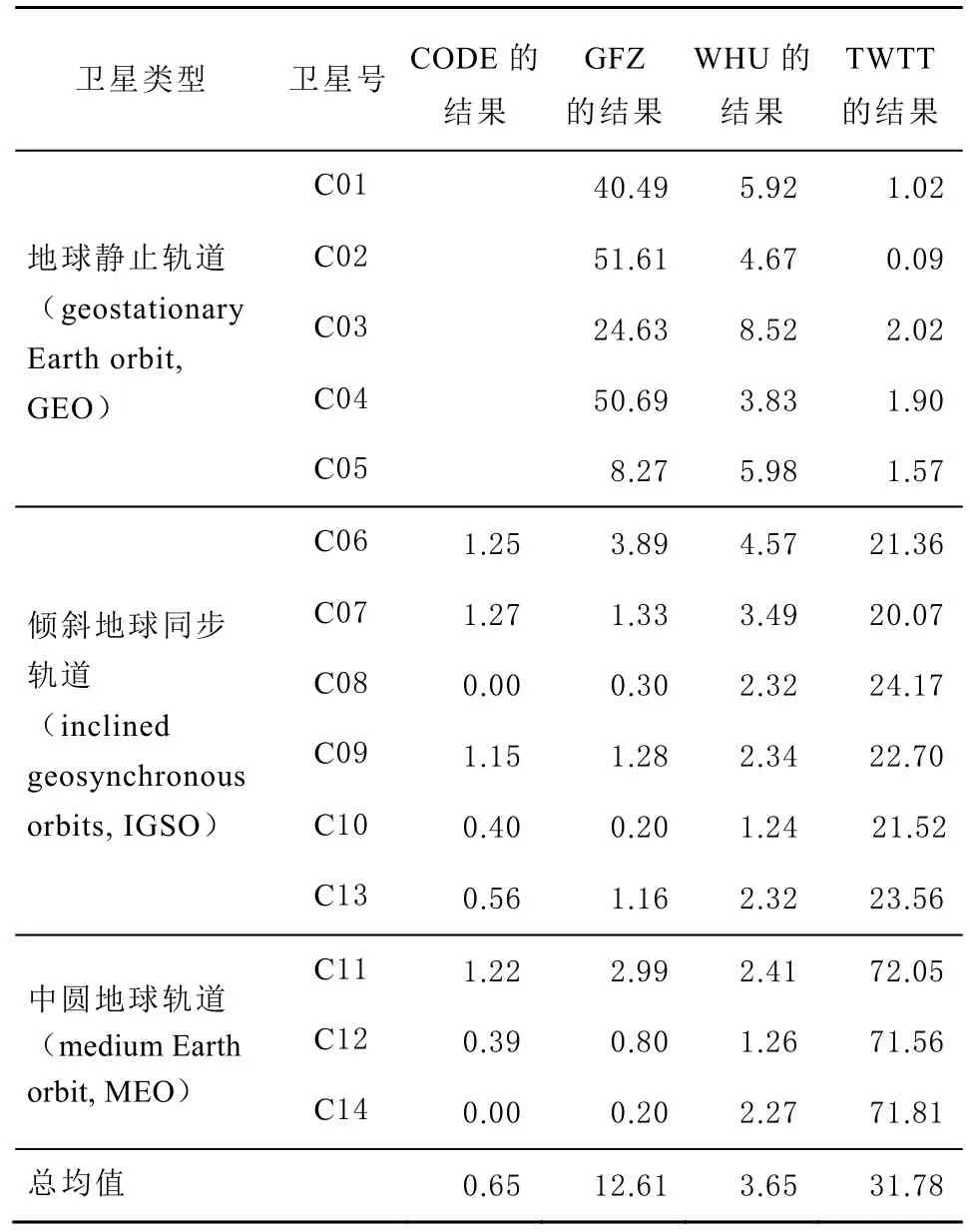
表 1 BDS 钟差数据缺失率统计表 %
由表1可知:
1)由于CODE不能提供BDS GEO卫星的星钟数据,所以在统计时均为空。
2)从统计表中可以看出,CODE对 IGSO和MEO的整体缺失率最低。
3)GFZ由于GEO卫星的可视性对GFZ跟踪站较差,所以 GFZ提供的 GEO数据缺失较为严重,最大缺失率可达50 %。而其提供的移动卫星的数据较为完整。
4)WHU提供的数据缺失率整体比较平均,GEO卫星的缺失率显著小于 GFZ的产品。但移动卫星的数据缺失率要逊色于另外 2个分析中心。分析其原因可能是,不同分析中心解算钟差所使用的测站不同,造成参与计算的可用卫星及其数量不同,导致不同分析中心的钟差产品数据缺失率存在差异。
5)CODE、GFZ和 WHU提供的星钟数据完整情况整体呈现出MEO卫星缺失率最小,其次为IGSO卫星,最后是GEO卫星的规律。
6)TWTT结果则呈现出 GEO卫星数据缺失率最少,MEO卫星数据缺失率最高的现象。由于GEO卫星在中国境内可连续跟踪,其数据最为完整。但当卫星出现异常时,其双向时间比对结果会出现短时中断。因此GEO卫星也存在数据缺失的情况。IGSO与 MEO卫星由于均涉及不可跟踪弧段且不可视时间不同,其数据缺失率与不可视时间成正比。
2.2.2 内附合精度
对单天的BDS卫星钟差产品采用2次多项式模型进行建模,获得单天的钟差拟合残差,并统计各卫星每天的钟差拟合残差的均方根误差。结果如表2所示。
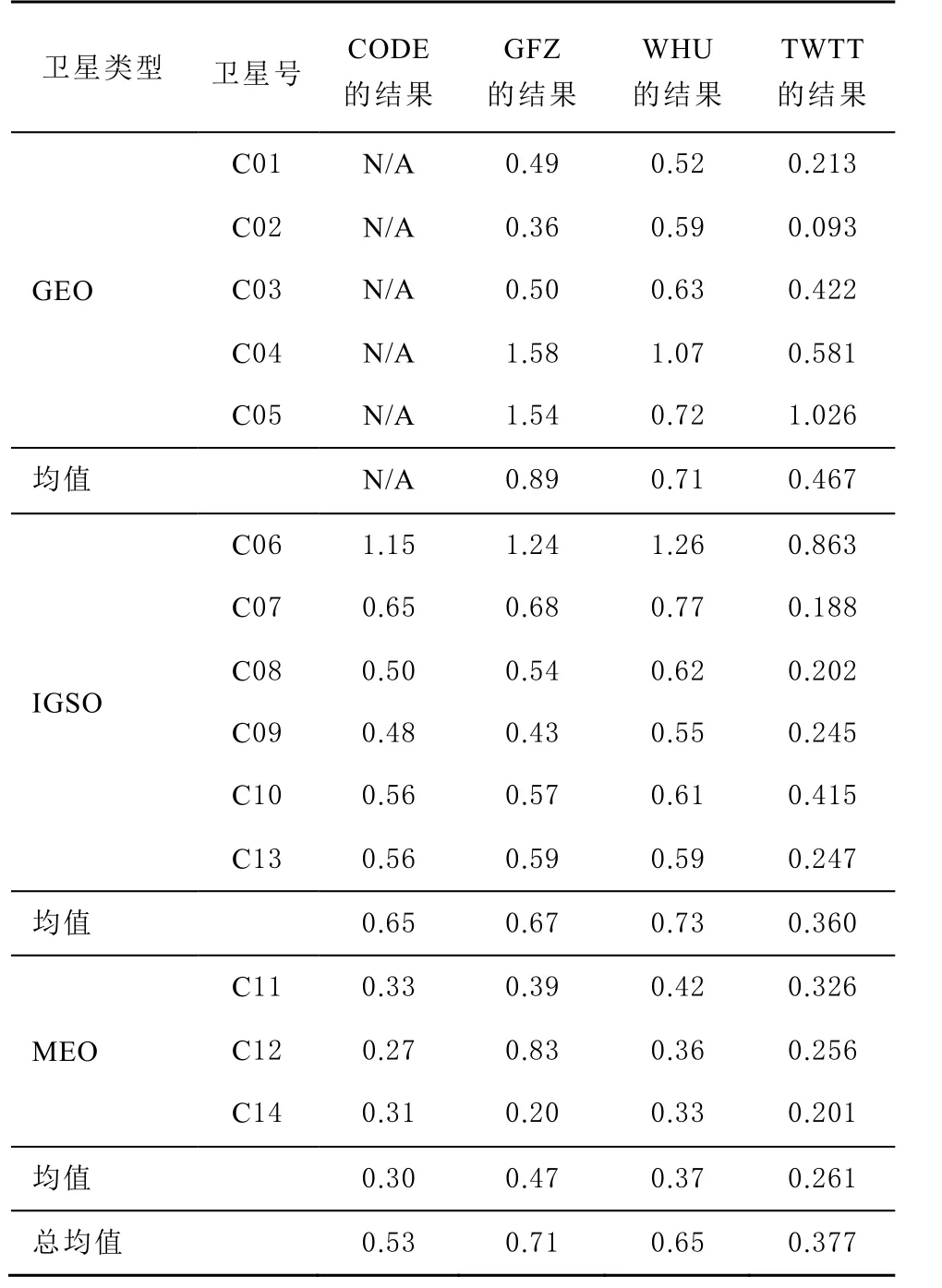
表2 BDS钟差数据内符合精度RMS统计表ns
由统计结果表明:
1)对于CODE而言,由于不提供BDS GEO卫星的星钟产品,其IGSO的拟合精度稍差于MEO卫星;对GFZ的产品而言,GEO卫星的钟差拟合精度稍逊于IGSO卫星,MEO卫星的拟合精度最佳;而WHU的产品则是MEO卫星拟合精度最好,IGSO卫星稍逊于GEO卫星拟合精度。其中C04、C05和C06 3颗卫星的单天拟合精度最差,拟合残差能达到同类卫星的2~3倍。
2)不同分析中心的产品存在差异,但内符合精度相当,均优于纳秒级,3者差异也优于纳秒级。体现出不同分析中心的产品具有较好的一致性。
3)总体上看 TWTT结果的内符合精度最高,优于3个分析中心的产品。且呈现出GEO卫星与IGSO卫星的钟差拟合精度相当,MEO的拟合精度最佳的结果。同时C05和C06的单天拟合精度最差,可达到纳秒级。
2.2.3 基于重叠 Hadamard方差[2,19-20]的数据稳定性分析
对已完成数据预处理的钟差数据进行频率稳定度分析。考虑到北斗二号卫星均使用星载铷钟,所以选取重叠 Hadamard方差进行频率稳定度分析,采样间隔取为300 s。结果如表3、图 1~图 4所示。
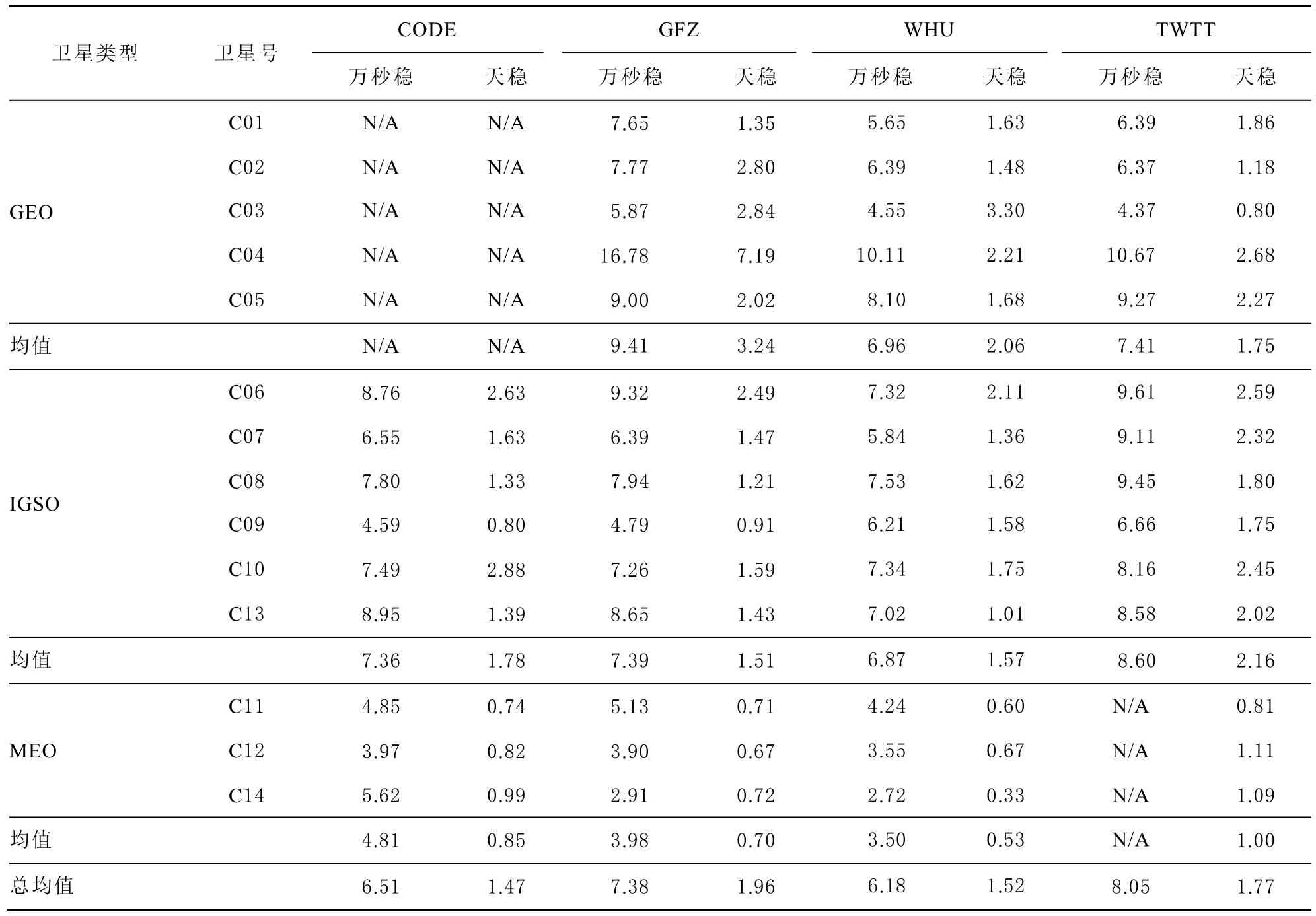
表 3 BDS 钟差数据频率稳定度分析统计表 1×10-14
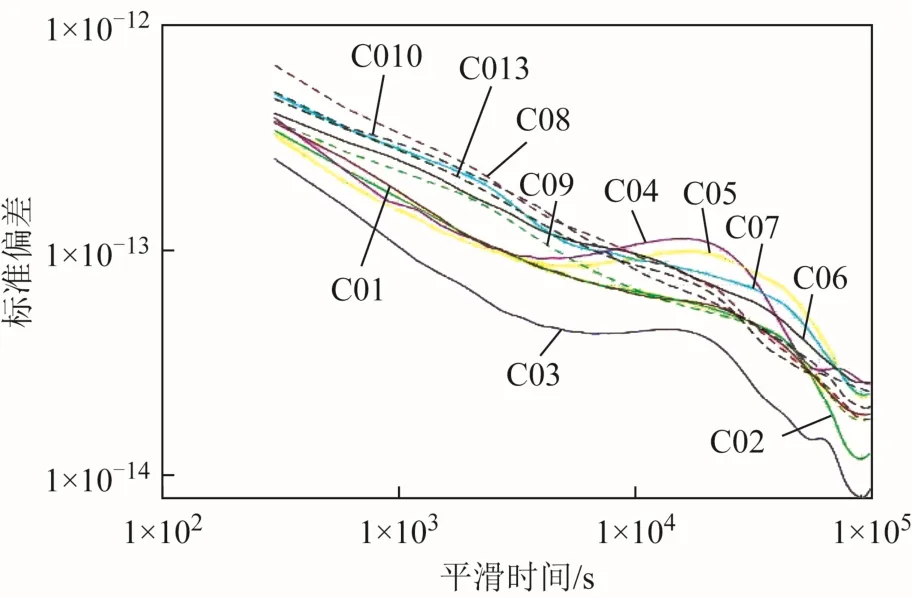
图 1 TWTT 数据频率稳定度分析
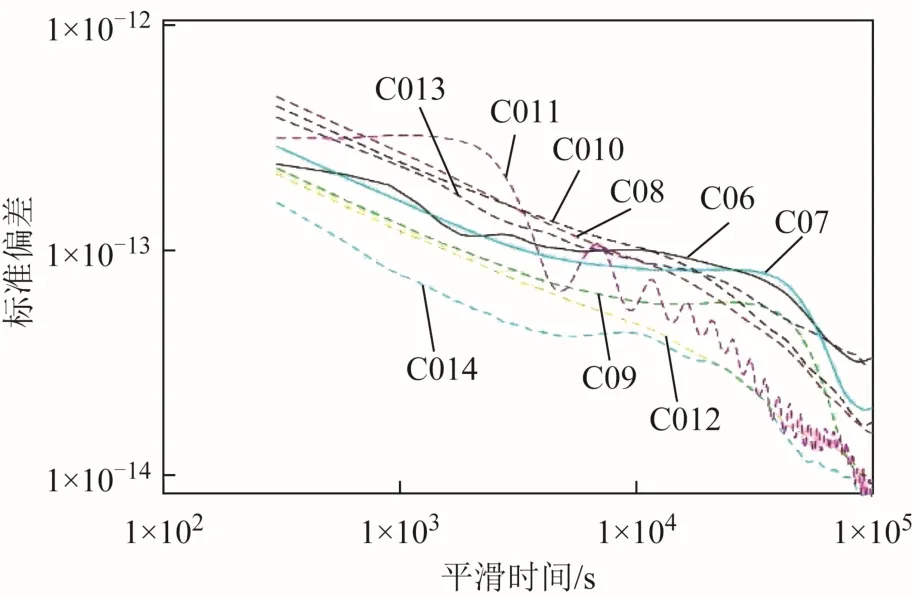
图 2 CODE 数据频率稳定度分析
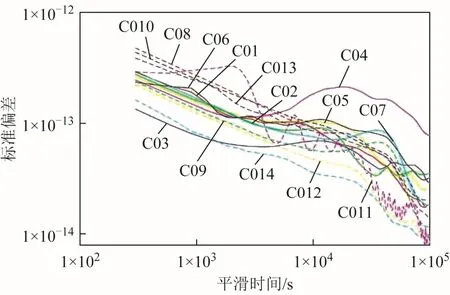
图3 GFZ数据频率稳定度分析
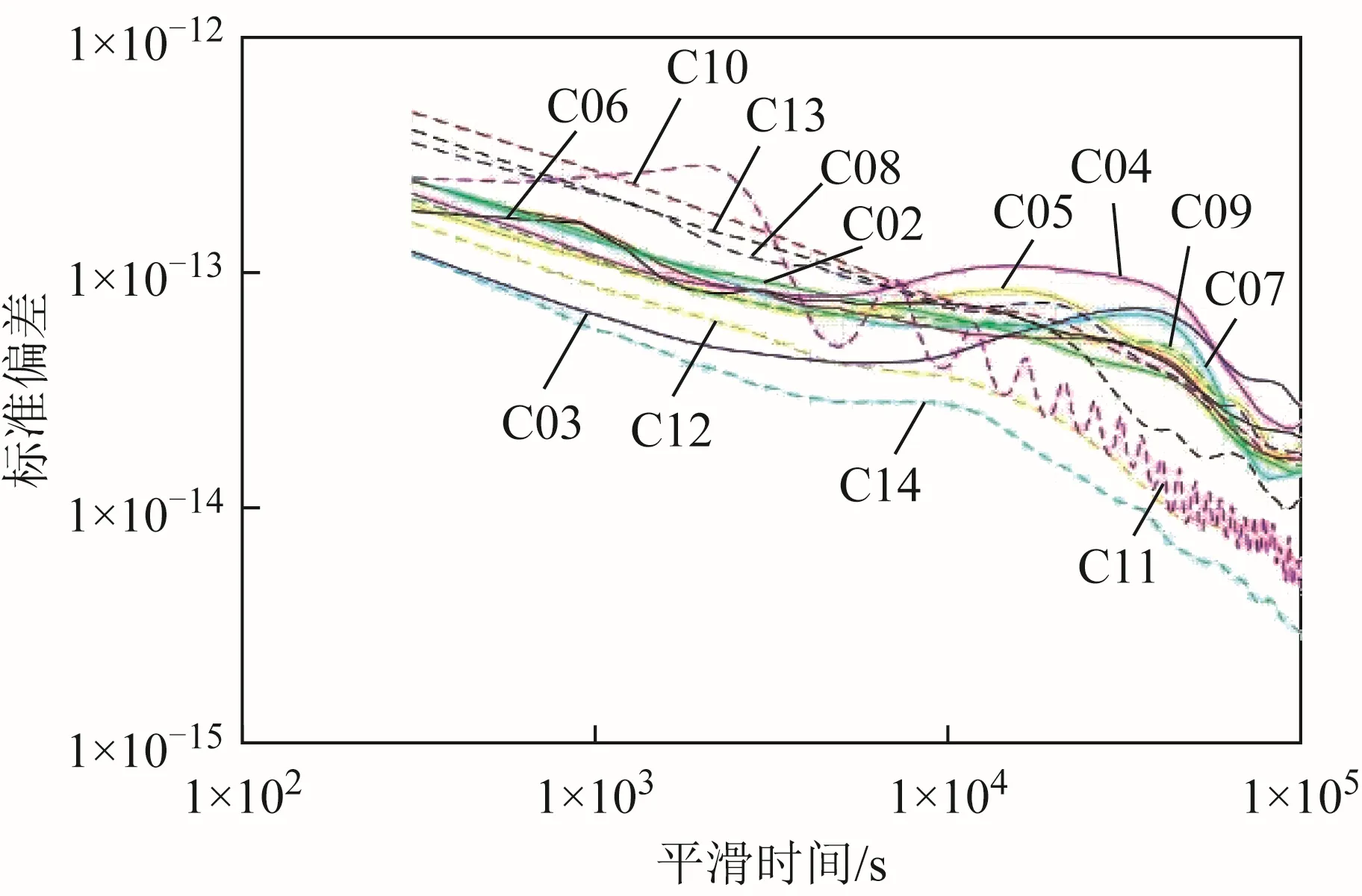
图4 WHU数据频率稳定度分析
由统计结果与上图可以看出:
1)由于TWTT的MEO卫星数据缺失严重,其结果仅作参考。
2)3个分析中心的频率稳定度结果呈现出高度相同的趋势,3者有较高的吻合程度。
3)结果中,C04卫星的稳定度较其余GEO卫星差,万秒稳达到1×10-13量级。C11卫星的稳定度呈现震荡的特性,明显异于其他卫星。
4)TWTT的结果中,由于GEO卫星的观测数据更为连续,于是稳定度结果要优于 IGSO卫星。而对于CODE、GFZ和WHU的结果中,钟差是由精密定轨解算得到的,致使移动卫星的稳定度结果要优于GEO卫星。
5)TWTT相较于3家分析中心的稳定度可以发现,在平滑初期3×102s≤τ≤103s的时间段内,TWTT受FLPM噪声的影响更为显著。
3 结束语
1)由于当前 BDS采用 TWTT方式进行星地时间同步,且受限于系统监测站分布的区域性,造成IGSO与MEO卫星数据存在较为严重的缺失。其中 GEO卫星数据缺失率均值为 1.32 %,IGSO卫星数据缺失率超过20%,MEO卫星数据缺失率超过70 %。而使用ODTS机制的CODE、GFZ和WHU的钟差产品数据缺失情况则呈现出MEO卫星缺失率最小,其次为 IGSO卫星,最后是 GEO卫星的规律。总体上,GFZ的钟差产品缺失率最高,CODE最低。
2)得益于双向时间比对技术,许多卫星到地面站之间的公共误差得到显著削弱,使得 TWTT的内符合精度优于CODE、GFZ和WHU的产品。就 TWTT而言,呈现出 GEO卫星与IGSO卫星的钟差拟合精度相当,MEO的拟合精度最佳。
3)3家分析中心星钟产品的时域稳定度结果相当,表现为MEO卫星稳定度最高,GEO卫星稳定度最低。TWTT结果则是GEO卫星稳定度优于IGSO卫星,由于MEO数据缺失严重,其结果仅供参考。4种数据的天稳均达到1×10-14量级。
4)虽然不同分析中心采用的数据处理策略会有不同,导致不同分析中心的产品略有差别,但整体上 3家分析中心的数据质量相当,在开展 BDS卫星星钟数据质量评估工作时,使用分析中心提供的BDS卫星钟差数据可以得到接近使用TWTT数据的结果。

