基于EMD的GNSS时间序列降噪软件实现
贺小星 ,熊常亮 ,常 苗 ,班 亚 ,李姝莹 ,邓心茹 ,邓丽红
0 引言
全球卫星导航系统(global navigation satellite system,GNSS)已经在各行各业中获得了广泛应用,近 20余年累积的全球 GNSS连续运行参考站(continuously operating reference stations,CORS)坐标时间序列为大地测量学及地球动力学研究提供了宝贵的基础数据[1-3]。GNSS CORS不仅是区域及全球高精度时空基准的重要基础设施,也是导航与位置服务、地质灾害监测、大地测量学与地球动力学等工程和科学研究的重要支撑[1]。GNSS CORS坐标时间序列不仅包含测站的线性变化,也包含非线性变化[4-7]。随着对大地测量成果所要求的精度越来越高,CORS坐标时间序列越来越受到关注。然而,GNSS时间序列数据处理工作非常繁琐且耗时,且很多重复性工作。另一方面,GNSS时间序列具有非线性、噪声成分与信号不易分离等特性[8],文献[9]所提出的经验模态分解(empirical mode decomposition,EMD)方法处理此类型的信号有一定的优越性。文献[10]将经验模态分解结合小波分解应用于 GNSS水汽时间序列,成功分析出不同周期性水汽振荡的成因。文献[11]对长周期地心运动时间序列进行 EMD分解,利用重构后的时间序列进行分析,提高了各运动方向的周期贡献率。文献[12]基于EMD方法精确提取了 GNSS高程时间序列的周期项。综上所述,EMD方法对于GNSS CORS坐标序列非线性变化精密建模具有重要意义,但在实际数据处理过程中缺少相应的分析软件。
基于此,为了增强软件的实用性、交互性,结合 GNSS时间序列降噪分析的基本原理及分析策略,开发出基于MATLAB的GNSS时间序列降噪软件:介绍了基于经验模态分解的 GNSS数据降噪基本原理,同时也给出了数据处理流程;软件包含多个时间序列降噪分析模块,交互性较好,可避免繁杂的计算工作,提高 GNSS时间序列数据处理及分析的效率。
1 基于EMD的GNSS时间序列降噪原理
1.1 EMD降噪原理
EMD方法应用于GNSS时间序列降噪,主要包括信号分解、分界本征模态分量判定、信号重构以及降噪效果评定4部分,降噪流程如图1所示。EMD降噪的基本思想是将信号分解为若干频率由高至低的本征模态函数(intrinsic mode function,IMF)和1个趋势项,趋势项与低频IMF分量重构可实现降噪。

图1 GNSS坐标序列EMD方法降噪流程
通常高频IMF中包含噪声信息,而低频IMF及趋势项包含信号的特征信息及趋势。在筛选过程中,每个IMF必须满足2个条件[12]:①序列中的极值点数目与过零点数相差不超过 1个;②由局部极大值构成上包络线,局部极小值构成下包络线,2者均值为0。然而,在实际信号分解过程中,第2个条件很难被严格满足,因此以1个阈值对条件2作替换处理,当IMF达到给定阈值时,就认为其满足条件2,阈值表达式为
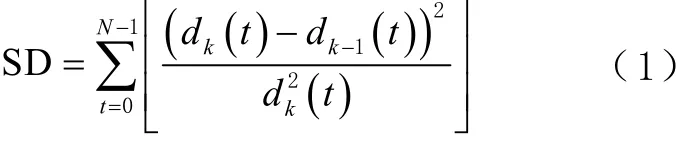
式中:SD为每个IMF停止筛选的阈值,通常情况下取 0.2~0.3;k为信号分量的序数;N为序列长度; dk(t)、dk−1( t )为每个IMF筛选过程中2个相邻的数据序列。
分解完成后的原始信号序列可由下式进行表示为
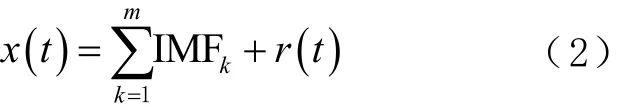
式中: x (t)为重构的原始信号序列;m为所有IMF分量的个数;r (t)为趋势项。依据相关系数准则判定分界本征模态函数。当相关系数第1次取极小值时,则其对应的IMF为分界IMF,并将其纳入至高频IMF分量进行重构。相关系数公式及重构公式为

式中:ρk为相关系数;xˆ(t)为EMD降噪后的“干净”的坐标序列;K为分界IMF分量的序号; r(t)为趋势项。
1.2 改进的EMD坐标时间序列降噪方法
针对EMD方法存在的模态混叠问题[13-15],进一步对EMD方法进行改进。假定原始数据序列设为χ1,运用EMD方法对其进行分解,改进的EMD降噪方法过程如下:
1)初始化:原始数据xi,i=1;
2)EMD分解,获取mi个IMF及趋势项ri(t);
3)计算相关系数,分界IMF为IMFiK;

7)i=i+1,xi=a;代入第2个步骤。
当 ki=2时循环分解停止,此时,将所有低频IMF分量及趋势项进行重构,得到降噪后的数据序列,可表示为
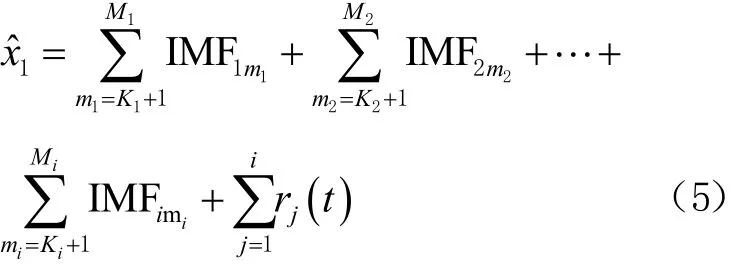
式中:xˆ1为降噪后的数据序列;Ki表示第i个原始数据序列的分界IMF下标; Mi表示第i个原始数据序列分解后 IMF分量的个数;IMFimi表示第 i个原始数据序列的第 mi个IMF分量; rj(t)表示第j次EMD分解的趋势项。
为定量反映方法的降噪效果,利用相关系数、均方根误差、信噪比等传统指标做出评价。相关系数越接近 1表明降噪信号与原始数据序列的相似程度越高,均方根误差值越小说明降噪信号与原始信号之间的偏差程度越小,信噪比值越大说明去噪效果越明显。均方根误差(root mean square error,RMSE)的计算公式为
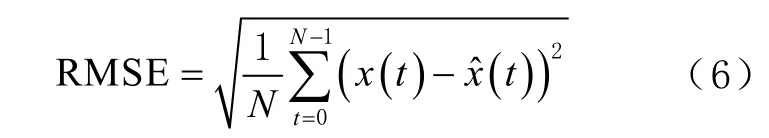
信噪比的计算公式为
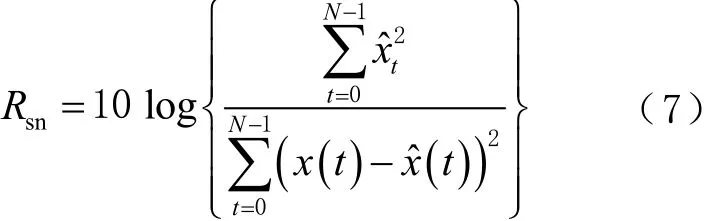
式中:RMSE为均方根误差;Rsn为原始序列与降噪后序列的信噪比。
2 基于EMD的GNSS时间序列降噪软件设计及实现
2.1 软件总体设计
根据 EMD理论设计基于 MATLAB的 EMD的GNSS时间序列降噪软件,软件总体结构如图2所示。软件主要包括数据导入、降噪分析与结果输出3大模块,每个模块下又分为几个小模块独立进行实现。各模块下设置若干子菜单,每个子菜单发挥不同的作用,共同完成单个模块的功能。不同模块间相互配合,通过融合与集成的方式,组成1个功能完整、操作简单的GNSS时间序列降噪软件。
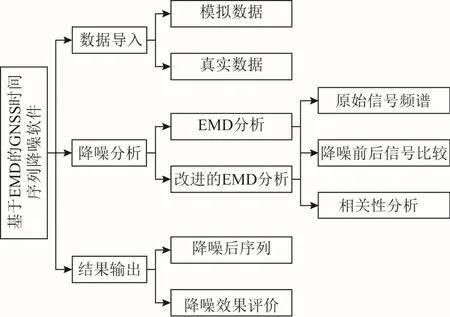
图2 软件结构
2.2 软件的实现
该软件充分利用MATLAB在矩阵运算、信号分析、图形绘制等方面的优越性,结合其图形用户界面良好的交互性进行开发,软件主界面如图3所示。
图3 基于EMD的GNSS时间序列降噪软件主界面
2.2.1 数据导入模块
在数据导入模块菜单下设有模拟数据与真实数据2种选择,其中真实数据可外部进行导入,支持多种数据格式,而模拟数据可设置为包括白噪声和多种有色噪声模型的信号序列,数据导入模块如图4所示。真实数据模块支持包括Excel与文本等多种格式的文件,无需其他操作即可完成数据的导入,真实数据导入界面见图5。
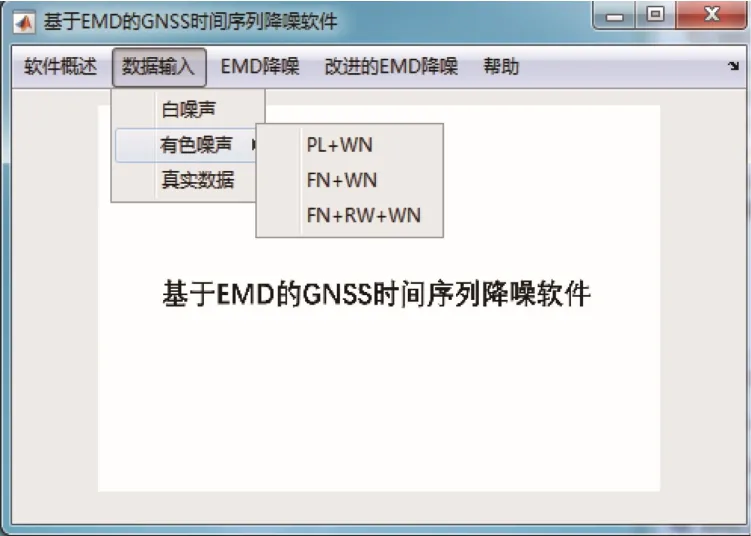
图4 数据导入模块
2.2.2 降噪分析模块
降噪分析模块是本软件的核心模块之一,该模块包括模拟数据分析、真实数据分析、结果输出3大功能。用户只需要点击软件菜单下对应的降噪分析按钮即可完成对载入数据的降噪处理,并自动绘制相关图形。鉴于目前针对于 GNSS时间序列降噪的方法多样性,本软件将上文介绍的EMD方法与改进的EMD方法各作为1个模块在软件中进行实现。 “数据分析”依据前述的EMD、改进的EMD方法对GNSS数据进行处理,并根据相关系数、均方根误差以及信噪比3个指标,依据式(3)、式(6)、式(7)对降噪效果进行评价。
2.2.3 结果输出模块
通过结果输出模块可输出包括各类图表在内的所有成果,同时为了提高用户操作的自由度,数据存储的路径可设置为计算机上任意路径,如图6所示。
3 测试分析
为验证软件的有效性与可靠性,对于同一含噪信号,利用软件中 2种不同的降噪分析方法对其作降噪处理。设置模拟信号噪声参数如下:序列长度 1 200,采样频率 1 Hz,高斯白噪声频率 4 dB模拟信号可表示为
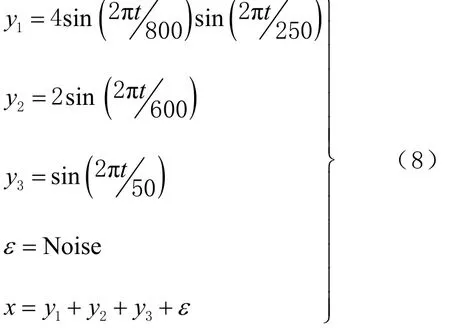
3.1 EMD降噪模块测试分析
数据导入之后,选择EMD分析菜单下的模拟分析,软件即自动对原始信号进行EMD降噪处理,同时绘制相关系数曲线如图 7所示,降噪前后的信号序列如图8所示。
降噪分析之后,软件将降噪后序列导出,同时依据前文所述的 3个评价指标对降噪分析的效果进行评估,如表1所示。因原始信号的真值已知,故降噪后信号与含噪声信号及真实信号分别计算各评价指标以定量的反映降噪效果。由表1可知,降噪后的信号序列均方根误差减小,信噪比与相关系数均增大,表明软件中进行的数据处理是行之有效的。
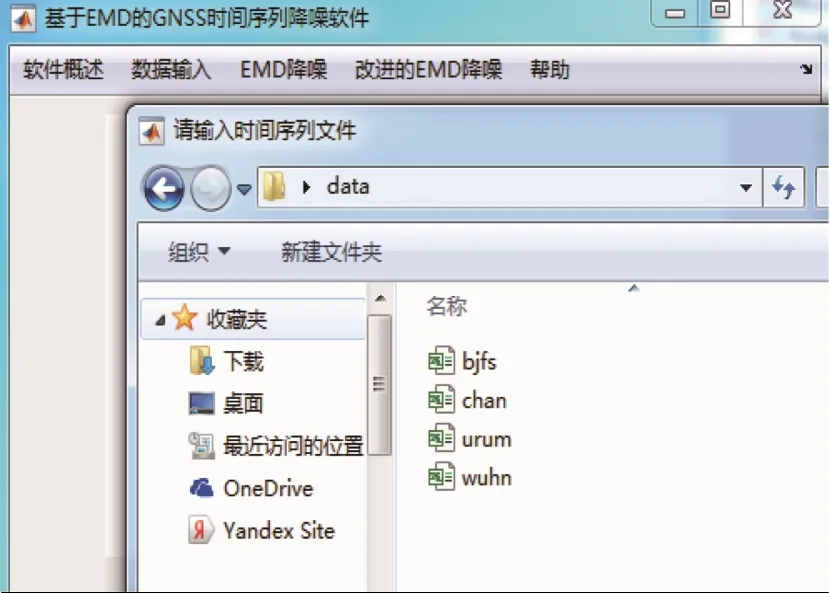
图5 真实数据导入

图6 选取文件保存路径
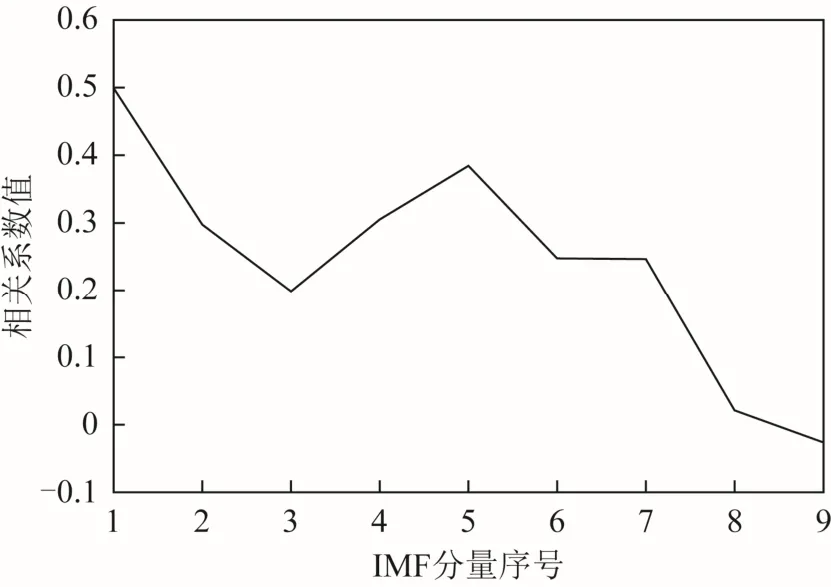
图7 相关系数曲线
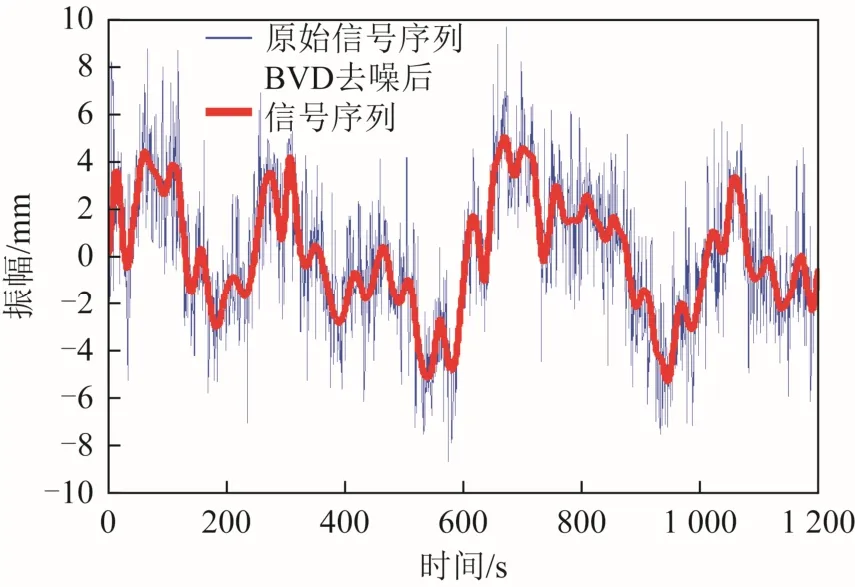
图8 降噪前后信号序列

表1 各评价指标值
3.2 改进的EMD降噪模块测试分析
将同样的数据利用软件所提供的改进的EMD方法进行降噪分析。默认情况下,EMD迭代分解次数设为3次,每次EMD分解所得的相关系数以及信号序列都由软件进行记录,并绘制图形,迭代分解相关系数曲线见图9,多次EMD分解前后信号序列见图10。
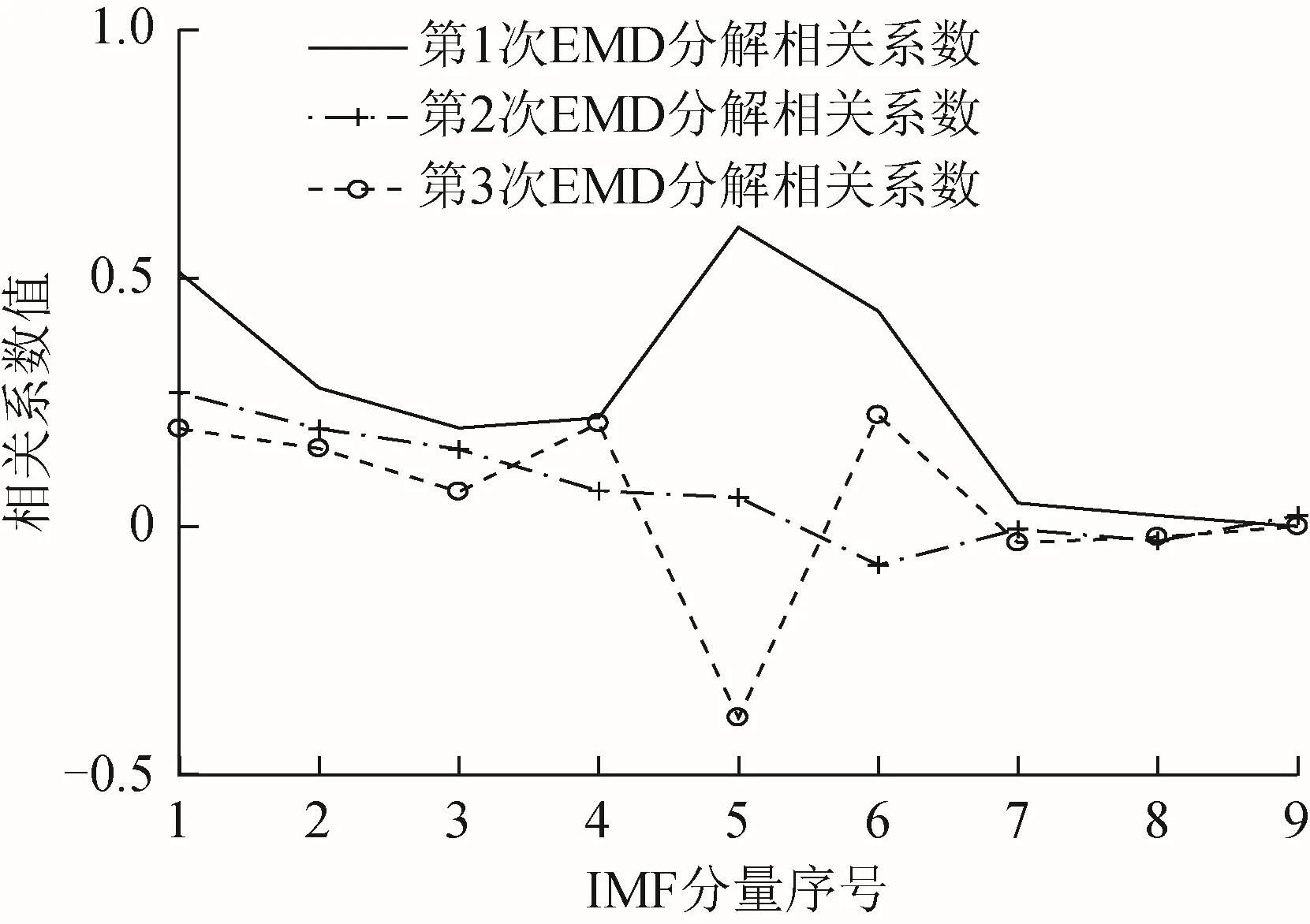
图9 迭代分解相关系数曲线
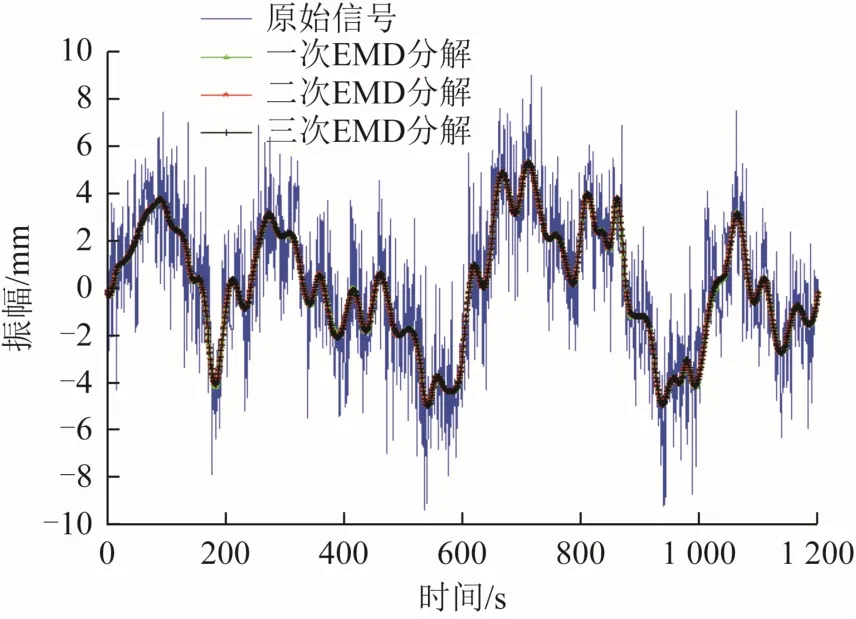
图10 多次EMD分解前后信号序列
每次 EMD分解后重构的信号序列都由软件进行保存,并计算各评价指标,以定量反映EMD分解次数对于降噪的影响,有助于选取降噪效果最好的信号序列。多次EMD分解后的评价指标值如表2所示。分析表2可知,进行3次EMD分解所获得的降噪信号较传统EMD分解所得降噪信号RMSE的值降低了0.016 7,相关系数提高了0.002,信噪比提高了 0.538 dB,说明该方法能够改善降噪效果,本软件也实现了数据处理与降噪分析的预期目标。
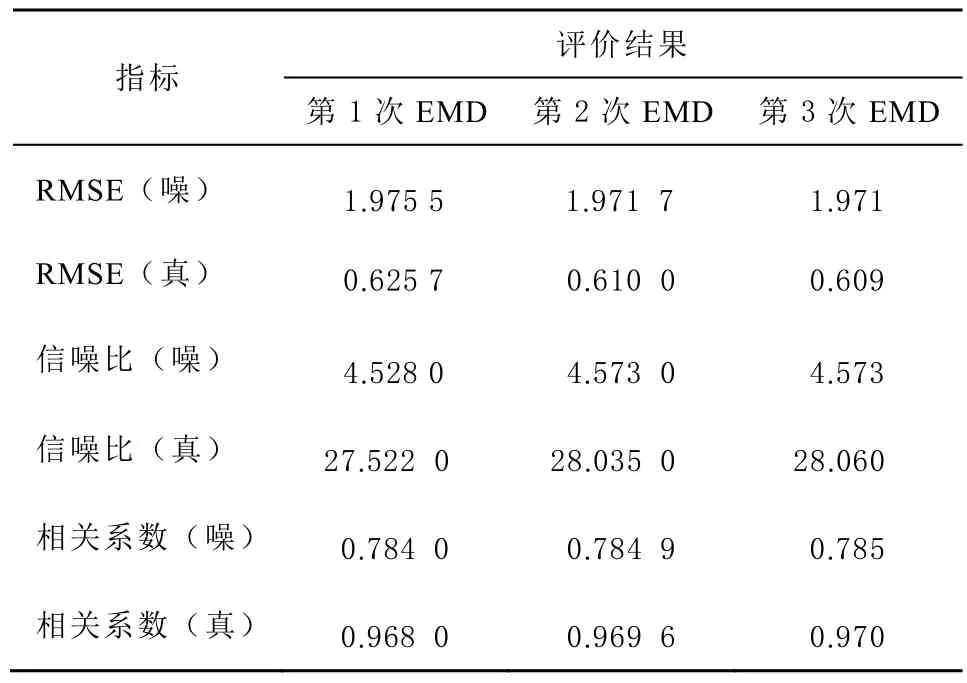
表2 各评价指标值
4 结束语
根据GNSS时间序列数据降噪处理相关原理,结合MATLAB开发了基于EMD的GNSS时间序列降噪软件,该软件采用模块化设计,功能较完善;在软件上基于仿真数据分别对传统EMD方法、改进的EMD方法进行实验分析,并利用均方根误差、相关系数及信噪比等传统评价指标判断降噪效果。软件测试实验结果表明:改进的EMD方法降噪后的信号序列比之传统EMD方法降噪的信号序列,RMSE的值降低了0.016 7,相关系数提高了0.002,信噪比提高了0.538 dB。该软件能够提高 GNSS时间序列数据处理及分析的效率,为进一步探索 GNSS基准站坐标序列非线性变化精密建模提供参考。

