兼顾语义的室内3维模型自动重建方法
史云飞,卞西蜀,张永翔 ,李雪飞,张丕亚
0 引言
室内导航是当前业界和学界的研究热点之一。室内导航需要解决的 1个关键问题是室内空间建模,它是实现室内导航的先决条件[1]。与室外数据模型相比,室内模型在空间尺度、组成要素、空间约束等方面具有自己的特征[1-3]。由于室内模型需要满足室内导航等需求,其模型应能区分哪些是可穿越边界(门),哪些是不可穿越边界(墙),这就需要模型具有语义特性,能够识别出墙、门等建筑部件。另外,拓扑是室内导航的1个重要部分,室内模型应该能够维护室内要素之间的邻接、连通等拓扑关系,从而可以将其转换为室内导航所需的各类节点关系图(node-relation graph,NRG),如连通 NRG、邻接 NRG等,以支持室内空间连通性、邻接性分析。因此,室内模型至少需要满足2个条件:①模型能够区分墙、门等建筑部件的语义;②模型应是拓扑数据模型,其基元需按照拓扑共享原则组织。
目前,3维(three dimension,3D)室内模型获取途径主要有3种:第1种是利用已有的楼层平面图和层高,借助 ARCGIS、SketchUp、AutoCAD、Revit等商业软件,通过人工建模的方式生成。此类重建往往成本高、效率低,需耗费大量的人力。第 2种是自动构建室内 3D模型,利用设计的算法自动生成3D室内模型,文献[4-8]的研究属于该类,但现有的研究没有顾及建筑语义,生成的 3D模型不能区分墙、门等建筑部件,不支持室内导航。第3种是从已有的建筑信息模型(building information modeling,BIM)中提取室内模型,文献[9-11]的研究属于该类,但这些研究的前提是已经存在室内BIM模型。本文尝试提出 1种使用已有楼层平面图自动生成 3D室内模型的方法,该方法在重建过程不仅顾及墙、门、窗等建筑部件语义,而且还按照拓扑共享原则组织3D数据。
1 室内建模特征分析与广义“推拉”概念
1.1 室内建模特征分析
室内空间通常是形体规则的棱柱体,其墙面垂直,顶面、底面水平。这种模型常用的生成方式是“推拉”。“推拉”是1种由低维对象生成高维对象的方法,它沿着1个方向从起始高度H“推拉”低维的几何(或拓扑)单形(如2维面)到终止高度L,生成高维单形(如3D体),[H,L]称为“推拉”间隔。现有绝大多数研究都是将“推拉”间隔设置在2维(two dimension,2D)多边形上,然后自下而上“推拉”多边形生成3D体。然而,由于这种“推拉”没有顾及不同建筑部件高度的差异性,生成的各个侧面(表示墙、门、窗等)等高,无法区分哪些面是墙、哪些面是门。图1(a)是1个表达房间的多边形,它带有1个门和1个窗;[0,3]表示多边形对应的“推拉”间隔。图1(b)是图1(a)“推拉”的结果,表示门、窗的侧面与表示墙的侧面高度都相同。而真正的门的高度是[0,1.8],窗的高度是[1,2.2],如图1(c)所示。显然,常规的“推拉”方式无法满足顾及门、窗等建筑部件语义的重建需求。
若要考虑重建兼顾门、窗等建筑部件语义的室内3D模型,就需要采用差异性的“推拉”方式,不能再将“推拉”间隔统一设置在多边形上,而是根据需要设置在多边形的各条边上。本文引入了广义“推拉”[12]来实现这种顾及建筑语义的3D重建。
1.2 广义“推拉”
若用I表示1维多面体对应的单位实间隔[0,1],Q表示I在“推拉”方向对应的1维正多面体:;设多面体P∈ρd,n的1个准分离(quasi-disjoint)剖分集是{Pi∈ρd,n},对于集合中的任意Pi,都对应Qi∈Q。广义“推拉”被定义为1个映射GE,存在:。此处的多面体是广义多面体,1维多面体为线段,2维多面体为多边形,逐次类推。{Pi∈ρd,n}表示嵌入到 n维空间中的线性正 d维多面体集合。准分离集是仅在边界上相交的点集,点集的正则化交集为空;{Pi∈ρd,n}是P∈ ρd,n的准分离剖分集,则∪Pi=P,且集合中的任意1对Pi与Pj存在,∂为取多面体的边界;表示并操作, Pi× Qi的并集构成了所生成多面体的1个准分离多面体剖分。
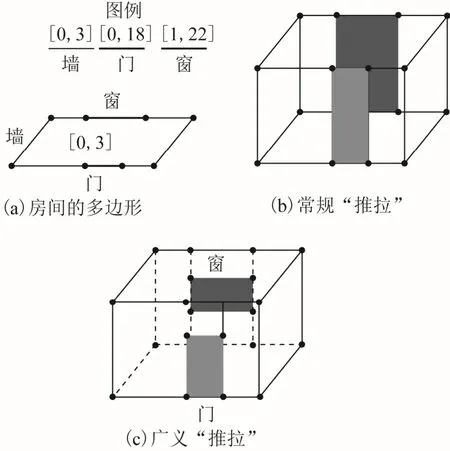
图1 “推拉”示例
广义“推拉”的实质是将待“推拉”的广义多面体剖分,形成1个准分离剖分集,并为剖分集中的每个元素指定1个“推拉”间隔,然后将每个元素按照它的间隔沿着1个方向“推拉”,生成新元素。在室内3D重建过程中,若将待“推拉”平面图边界 E ∈ρ1,3看作是由不同的边构成的1个准分离剖分集;每条边对应的起始高度和终止高度构成1个“推拉”间隔Ii=[Hi,Li],建筑物的起始高度H及其终止高度L构成1个间隔I=[H,L],存在Hi≥H,Li≤L。Ii可转换为1条“推拉”方向的线段 Qi:。如图 2(a)是平面图 1段边界的准分离剖分集, Qi是各条边对应“推拉”间隔。将 Ei沿着 Qi“推拉”对应的间隔,生成新3D单形,它们的并集仍然是1个准分离剖分集,图2(b)是图2(a)各条边沿着“推拉”间隔生成的3D面集。
2 基于广义“推拉”的室内3D重建
为将广义“推拉”引入室内3D重建,设计了以下重建流程,如图3所示。
2.1 创建3D结点
根据每个楼层所处的高度,为每张平面图设置1个起始高程。在将2D图形“推拉”为3D体的过程中,1个2D结点重建后可能对应多个3D结点,这些3D结点平面位置都与2D结点相同,只是高度不同。故平面图中的每1个2D结点对应1串 3D结点。为此,引入文献[13]提出的结点列概念,用符号Λ表示1个节点列,每1个2D结点对应 1个结点列。进一步的工作是为结点列中各个3D结点设置高程,而2D结点并不含高程,需从2D结点关联的2D边上间接获取。
常规建筑物平面图中,1个2D结点至少关联2条边,至多关联4条。每条边都对应1个“推拉”间隔,这些边的间隔可传递给2D结点。对于1个2D结点,取出与它关联的每1条边“推拉”间隔的左值与右值并排序,每个值加上楼层的起始高程即是1个3D结点的高程,每个高程与该2D结点的平面位置一起构建1个3D结点,同一平面位置上的3D结点形成了该2D结点的结点列。图4(a)是平面图及其对应的“推拉”间隔,楼层的起始高程为 75 m;图 4(b)是图 4(a)的 1部分,边 e1、e2、e3将高程传递给结点a、b、c和d;图4(c)中的点分别是2D结点a、b、c、d创建的3D结点。经过以上处理,得到平面图各个2D结点位置的3D结点列,同时也按从低到高的顺序完成了3D结点高程值的排序。
2.2 创建3D面
生成3D结点列后,进一步生成3D面。由于平面图中2D面的方向已经按照右手准则指定为向上,这也意味着多边形各条边的方向被确定。对于任意1个2D面,遍历它的每条边,获取当前边起始结点位置的3D结点列Λstart、终止结点位置的3D结点列Λend,从该边结点列Λend的起始高程H(Λend)处开始爬升搜索,到达1个新的3D结点Nnew后,获取该3D结点的高程值Hnew,然后到对面结点列Λstart中查找与Hnew等高的3D结点;若没找到,则返回到结点列Λend,从Hnew处的3D结点继续向上爬升。重复上述的过程,直至爬升到结点列最高处的3D结点,之后回到结点列Λstart中,从最高处开始降落搜索,直至降落到Λstart最低处的3D结点,搜索到的 Λstart和 Λend中的 3D结点围成的面即是该2D边对应的3D面。若在Λstart找到Hnew的对应结点,则直接回到结点列Λstart中,从Hnew对应的3D结点开始降落搜索,直至降落到结点列中位置最低处,搜索到的3D结点围成3D面。之后回到结点列 Λend,继续搜索更高位置的 3D面,从高度Hnew的3D结点继续向上搜索,到达新高度位置获取新结点Hnew’后,再回到结点列Λstart中,从Hnew’对应的3D结点开始降落搜索,直至到达Hnew处的3D结点,搜索到的3D结点又围成3D面,重复此过程搜索、构建更高高度的3D面。
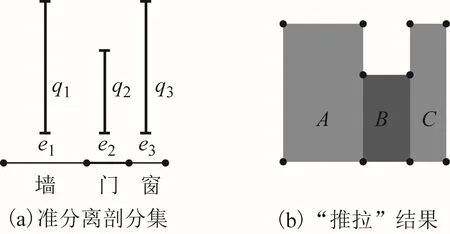
图 2 广义“推拉”示例
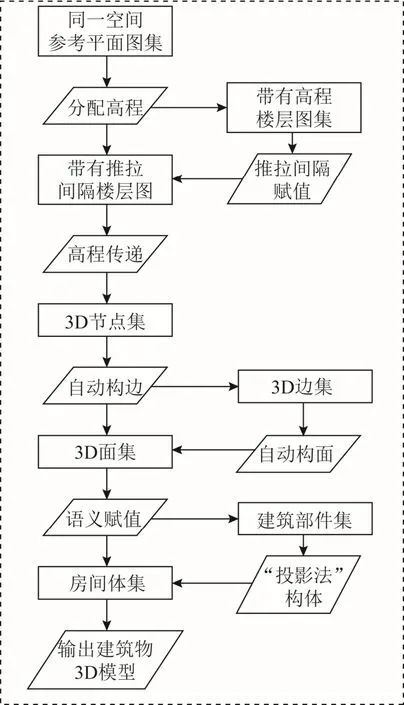
图3 室内3D重建流程
在搜索过程中,连接2个3D结点形成1条3D边。如果边是垂直边,则其方向指定为由低处指向高处,如果是水平边,则指定其方向和平面图中相应2D边的方向一致。从高处向低处搜索和从边终止结点向起始结点搜索时,不再创建新的 3D边,而是使用由相同3D结点已构造的3D边,只是在其前面标记“-”,表示与原来的边方向相反。3D面由生成的3D边围成,3D面的方向按照搜索3D结点的顺序,根据右手准则确定。
生成3D面之后需要为每个面赋予建筑部件语义。遍历每条2D边,找到当前边生成的3D面,若只有1个,则直接将2D边的建筑部件类型赋给3D面;否则,先计算当前2D边“推拉”间隔的左值与楼层起始高程的和,再分别取每个3D面高程值最小的3D结点(高程值最小的结点可能不止1个,任取其中1个)进行对比,找出后者与前者相同的3D面,并将2D边的建筑部件类型赋给它,剩余的3D面赋予墙。
图5为构建3D面的示意图,左图展示了3D结点与 3D面的方向,右图为完成构面的效果图。
在构建图4中2D边e1对应的3D面时,获取起点a的结点列Λstart(图5中A在的结点列)与终点b的结点列Λend(图5中B在的结点列),从Λend的最低处B开始爬升搜索,到达E,在Λstart中查找与E等高的3D结点,没有找到,返回到Λend,继续向上爬升,直至爬升到Λend最高处也就是G处,之后回到Λstart中,从位置最高处H开始降落搜索,直到到达Λstart的最低处A,Λstart和Λend中的3D结点{BEFGHA}围成1个3D面,根据这些结点的3D坐标值以及各结点的顺序在模型中创建相应的3D几何点、边和面。
在构建图4中2D边e2对应的3D面时,获取起点b的结点列Λstart(图5中B在的结点列)与终点c的结点列Λend(图5中C在的结点列),从C处开始爬升搜索,到I后,在Λstart中找到结点E与I高度相同,E为I的对应结点,从E降落搜索,直至降落到最低处B,Λstart和Λend中的部分3D结点{CIEB}围成 1个3D面。之后回到 C所在的结点列Λend,从 I处继续向上搜索,重复上述过程,又找了 2个结点序列{IJFE}、{JKGF}。最后根据结点序列创建边、面,如面 f1={AB,BE,EF,FG,-HG,-AH},f2={CI,-EI,-BE,BC},其方向均按照右手准则朝向外侧。
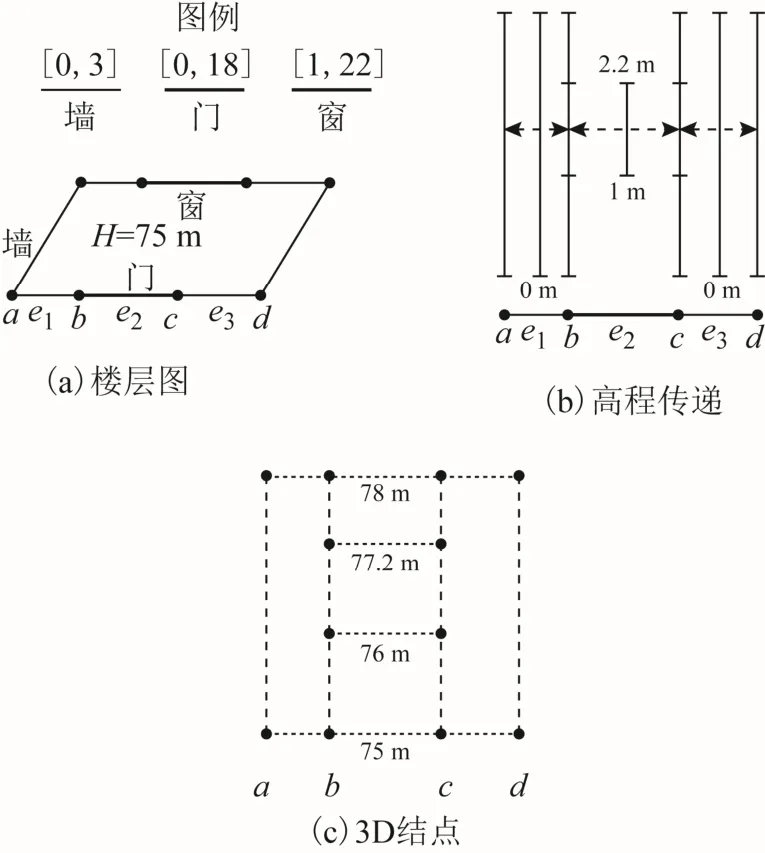
图4 3D结点的创建
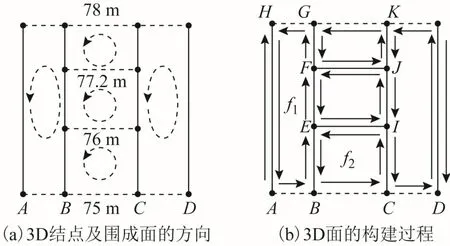
图5 3D面的创建
上述步骤生成了模型的各个立面,进一步构建水平面。水平面仅需在2个楼层之间构建即可,水平面中各结点的高程相同。前面已经生成了平面图中各2D结点对应的3D结点列,按照构成2D面的边的顺序,遍历每1条边,在每条边的每个2D结点对应的结点列中,找到高度最低以及最高的 3D结点,连接它们生成3D边与面,3D边的方向与2D边的一致,3D面的方向朝上。从本质上讲,同一高度的3D边构面与2D空间的多边形自动构建类似。
2.3 创建 3D 体
生成了模型的立面、水平面后,它们虽然在形式上围成了体,但并没有构建成体,而仅仅是NEF(node-edge-face)模型。需要进一步显式的表达体对象,也就是将围成体的面找出并组织成体。初始平面图中1个多边形重建后生成1个3D体,称为房间体,本文采用“投影法”查找围成1个房间体的面,具体步骤如下:
第1步:求取面内部点点集。遍历已生成的所有面,对于任意1个面,在构成面的结点中按照逆时针方向依次取3个不共线的结点:Ni-1、Ni、Ni+1,计算矢量叉乘Ni-1Ni×NiNi+1,若数值为正,则Ni为凸点,计算Ni-1与 Ni+1的中点Nmid,Nmid即为面内部的一点;若数值为负,则 Ni不是凸点,沿逆时针方向依次向后顺延1点,直到找到凸点为止。遍历完面后,获得内部点集{Nmid}。
第2步:进行投影。遍历平面图,以当前平面图为投影面,计算当前层最低高程值与最高高程值,搜索{Nmid}中结点的 Z坐标在范围内的结点集中每个结点向投影面作垂线,垂线与投影面的交点称为点的投影。投影后的结点会有2种情况:①落在投影面中某个多边形的内部;②落在多边形的边界上。实际操作中由于计算机存储浮点数问题,投影点可能并不是恰好落在边界上而是落在边界附近1个很小的邻域内,为此设置1个容差值,当落点与边界的距离小于容差值即视为落在边界上。
第3步:寻找离散面。在实际情形下每个多边形对应 1个房间体,遍历投影面中多边形,判断中落入当前多边形内部与边界的投影点,将落入多边形内部的点对应的面记为水平面,它们构成了房间体的顶面和底面;将落入边界上的点对应的面记为竖直面,它们构成了房间体的立面。为进一步验证找到的立面是否为当前房间体的面,判断是否存在公共边,若立面中的某个水平面存在公共边,则为当前房间体的立面,若没有公共边,进一步在中查找与 f邻接的立面,若这些立面中有 1个与中的某个水平面存在公共边,则也可以判断它是构成当前房间体的立面,这样就找到了当前房间体的所有面。
在体中各面的方向要朝向体的外部,由于之前创建水平面时已经将各面的方向指定为向上,对于创建的各水平面,如果其高程和该层最低高程相同,则为底面,其方向应向下,将其记为“-”,如果其高程和该层最高高程相同,则为顶面,记为“+”。通过“投影法”将围成1个房间体的离散面组织到一起,并指定了面的方向,完成了房间体的创建。
3 实验与结果分析
为测试提出的方法,利用Ruby语言开发了1个原型系统。实验选用1个小区作为实验数据进行测试,该小区有16栋建筑物,5种类型,涉及同构、异构、弧形、骑街等多种情况。实验使用的平面图为DXF格式,“推拉”前对平面图进行了预处理,保留了门、窗、墙等图层,删除了其他图层,并对图形之间的关系进行检查,剔除错误,然后对图层中各建筑部件的起始高度和“推拉”间隔进行了设定。实验使用的计算机的CPU为四核酷睿i7-4790 @3.6 GHz,内存为 16G DDR3 1660。图 6 是实验结果:图6(a)是类型Ⅰ,它是上下异构的建筑物,不同灰度的面表示不同类型的建筑部件;图6(b)是类型Ⅱ,它是上下同构的建筑物,对最上层进行了揭盖显示;图6(c)是类型Ⅲ,它也是异构建筑物;图6(d)是类型Ⅳ,属于跨街建筑物—骑街楼;图6(e)是类型Ⅴ,为拐角楼;图6(f)是寻面构体的实验效果。
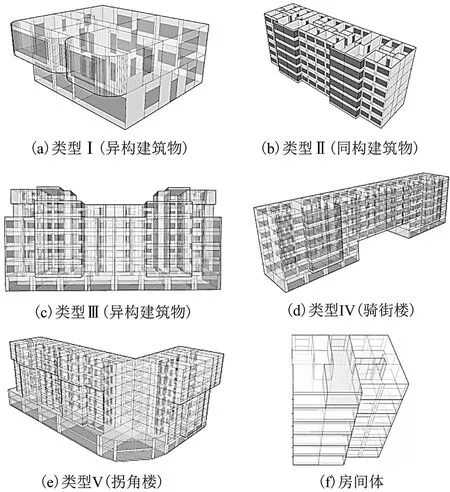
图 6 实验结果
实验对生成模型的结点、边、面、体以及耗时进行了统计,结果如表1所示。对于普通的6、7层的建筑物,重建时间小于10 s,整个小区16栋建筑物的重建共耗时约123 s。3D数据一旦生成后可多次使用,不用考虑实时生成的需求,所以算法的耗时可以接受。此外,生成的3D模型可根据需要导出MDB格式的数据库或skp格式文件。

表1 3D模型数据表
在构建楼层模型过程中,按照拓扑共享方式生成3D数据。图7是导出的3维模型数据:图7(a)是结点表,存储了节点的标识(identification,ID)和点的3D坐标;图7(b)是边表,存储了边的起点和终点,每条边记录其所引用结点的ID号;图7(c)是面表,存储了构成面的边的ID号;图7(d)是体表,存储了构成体的面的ID号。通过这些表可以看出,高维拓扑基元通过引用低维拓扑基元的方式构建。例如,结点表中高亮显示了2条记录,分别记录了8412号、8413号结点的信息。边表中高亮显示了8411号边的信息,该边引用了结点表中的8412号和8413号结点;面表高亮显示了10879号面的信息,该面的构建引用了8411号边;体表高亮显示了00000008号体的信息,该体的构建引用了 10879号面。通过结点→边→面→体递进引用的方式,实现了拓扑共享,减少了数据冗余,维护了拓扑的一致性。
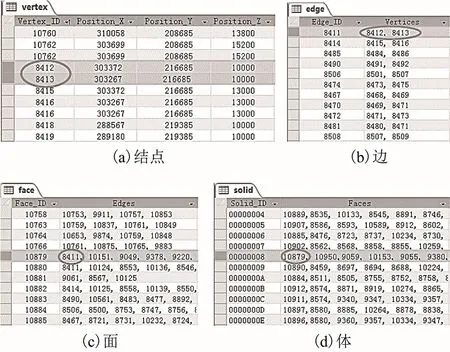
图7 模型导出3维数据
4 结束语
在不对现有建筑物直接3D测量的情况下,本文提出利用已有的2D图形资料,采用广义“推拉”的方式重建包含楼层、房间、门、窗等室内结构的建筑物 3D室内模型。该方法主要用于墙面垂直,顶面、底面平行的室内空间建模,而现实世界中的绝大多数建筑物属于该类;因此该方法具有较强的通用性。实验所采用的数据由当地房产测绘院提供。由于楼层平面图没有统一的空间参考,实验采用了同名点校正方法进行处理,即通过选取同一栋建筑物各个楼层平面图中相同位置的点(楼拐角、楼梯角等),并以实测分丘图(包含宗地边界和建筑物基地轮廓的地形图)中对应点为基准进行空间校正。校正后2D数据的精度主要受到3方面的影响:①分丘图中建筑物基地的精度,误差在5 cm以内;②图上选取同名点的图解误差,由于楼层平面图是矢量图,选取过程采用了捕捉模式,误差很小,可以忽略;③校正误差,即选取同名点后以楼基轮廓为基础进行楼层平面图校正,误差因选取的校正方法不同而不同。由于本文关注重点是重建方法,没有对校正误差进行深入分析,在进一步的工作中将对重建后的3D模型精度进行深入的探讨。
实验中仅涉及了门、窗、墙等建筑部件,现实世界中建筑物非常复杂,涉及多种建筑部件以及飘窗、跃层等复杂结构,下一步将添加更多类型的建筑部件进行测试,完善广义“推拉”算法,使之能支持更多类型的建筑部件重建。另外,当前实验中建筑部件“推拉”间隔采用了人工指定的方式,进一步将开发1个2D平面图预处理程序,在现有2D双线平面图基础上,提取单线平面图,并自动或半自动赋以“推拉”间隔,使得前期的数据处理更加自动化,从而提高整个建模的效率。

