基于BP神经网络的厘米级超宽带测距误差改正模型设计与实验

肖庭杨，章迪

( 武汉大学测绘学院，武汉 430079 )

0 引言

超宽带(UWB)是一种采用极低功率谱密度和极窄脉冲宽度的无线通信和定位技术，具有穿透能力强、传输速率快和时间分辨率高等优点[1]，理论上可以实现cm 级的测距定位. 但由于室内环境复杂，UWB定位受多路径等非视距误差影响较大，这类误差成为制约其定位精度的主要因素.

为提高UWB测距精度国内外学者展开了多方面的研究.文献[2]引入最小二乘残差法对粗差观测数据进行剔除，但不能有效地处理系统误差；文献[3]分析了UWB非视距误差的特性，提出了滑动窗口识别、动态调整噪声参数的卡尔曼滤波算法进行误差补偿，但单独改正效果不显著，需要函数拟合等方法进行进一步改正系统性误差；文献[4-6]利用多项式函数、指数函数等对测距误差进行建模，只考虑了测距误差和测距值之间的相关性；文献[7-10]从信号波形、信号接收强度、量测接收信号的随机性等方面出发，利用小波神经网络、支持向量机等机器学习方法估计测距误差，模型较为复杂；文献[12-14]将UWB与惯性传感器进行组合以削弱非视距误差的影响，需要额外的硬件支持，增加了算法复杂度；文献[11]提出一种神经网络改正模型，将测距值分解为两个分量作为模型输入但忽略了高程改正.

综上所述，现有的UWB 误差改正方法还存在应用范围较窄、改正精度有限和模型过于复杂等问题.基于此，本文建立了适用于三维空间的UWB测距误差BP神经网络改正模型，并且分析比较了两种不同网络结构的模型改正效果.

1 实验原理

1.1 BP神经网络模型

人工神经网络由输入层、输出层和至少一个隐藏层组成，每一层至少由一个神经元组成.BP神经网络能在输入和输出端建立一种非线性的映射关系，算法步骤如图1所示.

图1 BP神经网络算法流程图

1.2 最小二乘定位算法

2 精度评定

2.1 测距精度评定

以测距误差均值和均方根误差(RMSE)评定测距精度，计算方法如式(3)、(4)所示：

2.2 定位精度评定

选取RMSE评定X、Y、Z方向定位精度，如式(5)～(7)所示：

3 实验方案

3.1 实验设备

实验设备如图2所示，UWB 设备采用DecaWave公司的DecaWavePG1.5 套件；全站仪使用Leica MS50，测角精度为1″，测距精度为0.6 mm+1×10−6.

图2 实验硬件设备

3.2 实验场地

实验地点位于8 m×12 m 的室内场地，在4个墙面上各设置1个基站，在地面设置一系列网格点，包括1 个长时间测距点、42个采样点和5个检核点，如图3所示.长时间测距点用于测试测距的稳定性，采样点用于参与BP神经网络训练，检核点用于检验BP神经网络效果.

图3 网格点分布

3.3 实验流程

1)获取坐标及距离参考值

利用MS50全站仪测量各UWB基站和网格点的坐标，并通过坐标反算求得标签与各基站间距离的参考值.

2)测距稳定性测试

将UWB标签置于长时间测距点上，进行采样率为10 Hz、持续50 min 的数据采集，得到30 000历元的数据，对测距稳定性进行分析.

3)网格点数据采集与测距误差分析

利用UWB标签对采样点和检核点进行逐一测量，采样率为10 Hz、持续30 s，每点可获得4×300=1 200个测距值；将测距值减去步骤1)中得到的参考值，对测距误差进行统计分析.

4)网络建模与样本选择

建立两种模型：BP1 模型的输入节点数量为4，

5)模型训练与比较分析

将42 个采样点上的UWB测距值和坐标分别输入两个模型进行训练.5 个检核点的数据不参与训练，用于评价模型的测距误差预测精度；进一步利用改正后的测距值进行定位解算，与参考坐标求差，统计定位精度.在检验BP2时，假定各检核点的参考坐标未知，先利用UWB原始测距值通过最小二乘法得到检核点的概略坐标，输入训练好的BP2网络模型，分别得到其与4个基站间的测距改正值，对4个测距值均进行改正后，再进行最小二乘解算，并代入BP2模型中，重复上述过程，直至坐标变化量小于10−5.一般迭代5～8次后即可收敛.

整体实验设计方案如图4所示.

图4 实验流程图

4 实验结果

4.1 测距稳定性分析

将标签50 min 的连续测距值与全站仪测定的距离值求差，差值序列如图5所示，其与4个基站间距离误差的统计信息如表1所示.由图5可知，测距误差较为稳定.由表1可知，标准差远小于误差均值，即测距误差随时间变化幅度远小于测距误差本身，因此在各采样点上进行30 s的数据采集可以较为真实的反映其测距性能.

表1 长时间测距点上测距误差统计

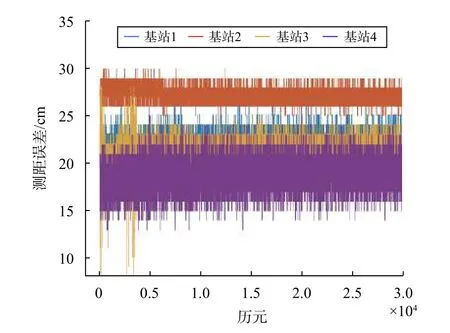
图5 单点测距序列

4.2 测距精度分析

1)测距误差统计

将所有网格点的距离测量值(共计42×300×4=50 400个)与全站仪测得的距离值作差，统计其均值和RMSE，结果如表2所示.

表2 测距误差统计cm

由表2可知，实验使用的UWB测距误差的均值约为26 cm，RMSE值约为20～30 cm，最大可达56 cm，最小为3.2 cm，存在一定的系统性偏差，即总比参考距离要大.这主要是因为受到室内多路径等非视距因素的影响，标签与基站3之间的测距误差明显大于与其他基站间的测距误差，这是因为基站3附近存在一较大反射面(60寸液晶电视屏)，非视距误差偏大.

2)测距误差与距离相关性分析

为分析测距误差与距离之间的相关性，以网格点到基站的距离为横轴，对应的测距误差均值为纵轴，绘制散点图，如图6所示.

图6 误差-距离散点图

由图6中可知，测距改正值和距离之间不存在明显的线性相关性.同一基站的测距值，距离大的误差不一定比距离小的误差大，反之可能更小.因此不能简单地在测距值和误差之间建立线性改正模型.

3)测距误差空间相关性分析

以网格点对某一基站的测距RMSE为半径绘制测距误差圆，每一子图对应一个基站，如图7所示.

图7 网格点测距误差圆

由图7可知，对同一基站，不同网格点的测距RMSE 并无明显的空间分布规律，但不同基站间普遍呈现出一定的误差分区现象，只是区域划分各有不同，可见基站和网格点坐标对测距误差均有影响，可将二者同时作为BP神经网络的输入，来拟合这种测距误差的非线性分布.

4.3 BP 神经网络对比分析

4.3.1模型训练效果对比

模型训练结果如表3所示.

表3 模型训练状态

由表3可知，BP2相关系数比BP1大0.11，更接近于1，这说明BP2有更好的拟合效果.

4.3.2测距改正精度对比

统计得到各测试点上标签与所有基站的测距精度指标，结果如表4所示.由表4中可知经模型BP1、BP2改正后测距RMSE 明显减小，相对于改正前，BP1平均减少83%，BP2平均减少91.7%.

表4 测距精度cm

4.3.3定位精度对比

统计所有测试点改正前后X、Y、Z方向的定位RMSE，统计结果如表5所示.

由表5中可以知，相对于改正前的RMSE，X方向上BP1减少72.7%. BP2减少93.8%；在Y方向上BP1减少73.7%，BP2减少91.2%；在Z方向上BP1减少81.2%，BP2减少96.3%.

表5 测试点定位精度cm

以测试点T1为例，测距值经BP1、BP2改正前后，坐标散点图分布如图8所示，其改正后的X、Y、Z方向误差序列如图9所示.

图8 测试点T1改正前后平面坐标散点图

可以看出，进行误差改正前，定位解算点明显偏离参考坐标；利用BP1、BP2改正后解算点位与参考坐标间偏差均明显减少，且BP2解算点与参考点更加接近、分布更加集中.

从图9中可以看出在T1上，相对于BP1，BP2在Z方向精度提升幅度最大.

图9 测试点T1定位误差序列

5 结束语

UWB测距误差是基站坐标和标签坐标的复杂函数，难以通过常规方法建立精确改正模型.本文作者借助BP神经网络强大的非线性拟合能力，建立了两个不同网络结构的误差改正模型，以高精度全站仪测量结果作为模型训练和对比测试的参考，实验结果表明：两种模型均能有效地改正测距误差，提高定位精度.BP2模型以标签、基站坐标作为输入，相比以4个距离作为输入的BP1模型，改正效果更加明显，三个方向的定位精度均由改正前的dm 级提升至cm 级；且BP2模型的输入不受基站数量限制，使其应用也更为灵活、适用性更强.需要注意的是，改正效果好的前提是室内环境没有明显变化，否则应重新进行参考值测定和模型训练.