大学数学类课程思政探索与实践

杨威 陈怀琛 刘三阳 高淑萍 李兵斌

[摘要]为了做好、做精大学数学类课程思政工作，分析了大学数学类课程开展思政教育的劣势和优势，以西安电子科技大学线性代数课程教学为例，从课程思政顶层体系设计理念出发，提出大学数学类课程思政建设的五条思路：从特殊数字出发、从数学发展史出发、从中国科学家故事出发、从马克思主义哲学思想出发、从数学具体知识点出发，深度挖掘课程思政元素。最后给出了16个课程思政的案例，为线性代数课程思政提供了充足教学素材，也为大学其他数学类课程提供了很好的借鉴。

[关键词]大学数学类课程;线性代数;课程思政

[中图分类号]G642

[文献标识码]A

[文章编号]2095-3437（2020）03-0077-03

新时代中国高等教育必须把立德树人作为教育的根本任务，培养什么人、怎样培养人、为谁培养人，是高校在人才培养目标过程中必须回答好的根本问题。习近平总书记在全国高校思想政治工作会议上指出，要用好课堂教学这个主渠道，使各类课程与思想政治理论课同向同行，形成协同效应。由此，课程思政作为一种教育理念，逐步在高等教育界形成共识。大学所有课程教学都肩负价值引领的责任。课程思政旨在充分挖掘各类课程中的思想政治教育元素，充分发挥所有教师和课程内在的育人功能，形成全员、全方位、全过程育人的教学体系。但由于“课程思政”实践探索刚刚展开，还存在诸多问题有待解决。

一、大学数学类课程的特点

相对其他课程而言，大学数学类课程有其自身的特点，在开展课程思政建设方面存在一些優势和劣势。

（一）大学数学类课程开展思政教育的劣势

数学教学立足于规律的普遍性，大学数学类课程本身研究客观存在的自然规律，超越意识形态，具有通约性和普遍性;另一方面，在大学数学类课程的教学中，对基本概念和理论，运算方法和技巧的掌握有明确的要求，学生接受的教育重点在知识层面。这使得大学数学类课程难于开展课程思政的教学。

（二）大学数学类课程开展思政教育的优势

大学数学类课程开展课程思政也有其优势，表现在：1.课程本身性质重要，属于大学期间最重要的基础课，大学生们也非常重视数学类课程的学习，所以在这些课程中展开思政教育，把课程思政做好，就更有意义。2.课程对象人数多，是所有理工农医及经管类专业的必修课，其涉及面广泛。以西安电子科技大学为例，全校针对97%的学生开设数学类课程，数学类教学团队把课程思政做好做精，就能使得思政教育的效率更高、效果更好。3.课程对象年龄小。以西安电子科技大学为例，高等数学、线性代数及概率论和数理统计分别在第一、第二和第三学期开设，而思政教育开展越早收效就越好，所以数学类教学团队要抓住这个时机。

二、西安电子科技大学线性代数教学改革简介

从2005年开始，西安电子科技大学对线性代数课程进行了长期、持续的改革与探索。2009年陈怀琛教授负责教育部“使用信息技术工具改造课程项目”一用MAT-LAB和建模实践改造工科线性代数子项目带动了全国19所大学进行改革试点，其改革成果得到教育部数学教指委的高度认可间;2009年刘三阳教授负责的线性代数获国家级精品课程;2017年杨威副教授负责的《实用大众线性代数》获首批国家精品在线开放课程，该课程从2016年10月至今已经在中国大学MOOC平台连续播放七期，学员总数达八万余人，获得了广大学员的高度好评。

三、西安电子科技大学线性代数课程思政建设理念

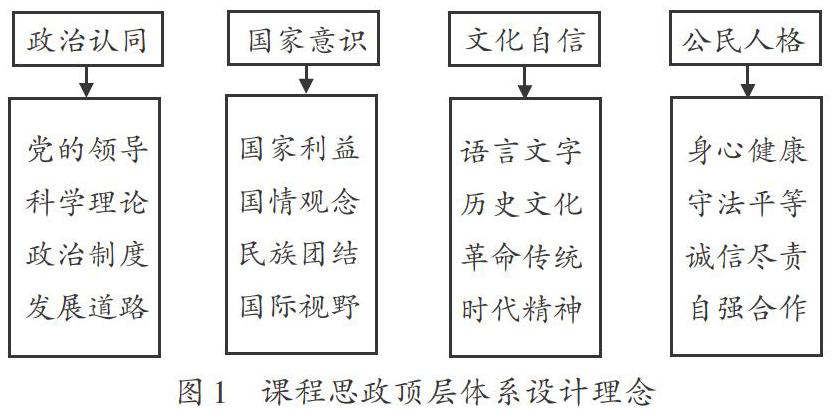
2019年春季，西安电子科技大学全校共有59个线性代数教学班，任课教师共54名，很多教师自身对思想政治教育内容理解不深刻，存在思想误区，所以明确课程思政的顶层体系设计理念是做好课程思政的必要条件。图1从四方面阐述了课程思政顶层体系设计理念。

西安电子科技大学线性代数教学团队在原副校长陈怀琛教授和国家级教学名师、国家级线性代数精品课程负责人刘三阳教授带领下，从课程思政顶层体系设计理念出发，精心设计教学内容，利用各种教学方法把思政元素全方位、全过程地贯穿在整个课程中，使思政教育做到润物细无声，将价值观培育和塑造“基因式”地植入到大学线性代数课程中。

四、西安电子科技大学线性代数课程思政建设内容

西安电子科技大学线性代数教学团队深入挖掘、系统梳理和精准厘定线性代数课程中蕴含的思政教育资源及其核心内容。

（一）从特殊数字出发，挖掘思政元素

从特殊数字出发，巧妙引出“革命传统”和“国家意识”等思政元素，帮助大学生树立正确世界观、人生观和价值观。

分析：教师在讲授完矩阵基本知识后，分析矩阵元素，引出思政教育内容。

西安电子科技大学前身是1931年诞生于江西瑞金的中央军委无线电学校，是毛泽东等老一辈革命家亲手创建的第一所工程技术学校，培养学生作为一名西电人的自豪感。

（二）从数学发展史出发，挖掘思政元素

从数学发展史出发，引出中国历史文化，树立文化自信和民族自豪感。

案例2.在学习线性方程组、矩阵及矩阵的初等变换时，教师可以介绍中国著名数学著作《九章算术》。

分析：《九章算术》成书于公元一世纪左右，书中第八章“方程”采用分离系数的方法表示线性方程组，相当于现在的矩阵;解线性方程组时使用的直除法，与矩阵的初等变换一致。这是世界上最早的完整的线性方程组的解法。在西方，直到17世纪才由莱布尼兹提出完整的线性方程的解法法则。通过这个案例，弘扬了中国文化，增强了学生民族自豪感、文化自信心和爱国情怀，也提高了学生学习线性代数的热情。

（三）从中国科学家故事出发，挖掘思政元素

从中国科学家故事出发，引出国家意识，树立爱国情怀、歌颂自强不息的精神。

案例3.在讲解知识难点和易错知识点时，教师可以引出中国科学家王中林的故事。

分析：王中林是国际顶尖纳米科学家、能源技术专家，中国科学院院土。他是能源诺贝尔奖第一位华人获得者，是西安电子科技大学培养出来的科学家，当他发明了纳米发电机后感慨到：“有时候你摔了一跤，但绊倒你的很可能不是砖头，而是一块金子。”通过王中林的人格魅力和科学精神，鼓励学生要正确面对挫折和失败，敢于探索、刻苦钻研，为祖国的繁荣和强大而努力学习。

（四）从马克思主义哲学思想出发，挖掘思政元素

从马克思主义哲学思想出发，挖掘线性代数课程中“变与不变”、“量变与质变”等辩证关系，让学生懂得：学好辩证法是深入理解线性代数概念的关键。

案例4.在学习矩阵初等变换、矩阵相似变换及矩阵合同变换时，教师可以引出“变与不变”的辩证关系。

分析：矩阵进行初等变化，秩不变;矩阵进行相似变化，特征值不变;矩阵进行合同变化，正、负惯性性指数不变。这就是所谓“形变质不变”的辩证思想。

案例5.在判断矩阵是否可逆、方程组是否有解、二次型是否正定时，可以引出“以量定质”的辩证思想。

分析：根据行列式的值来判断矩阵可逆性;根据方程组系数矩阵和增广矩阵的秩来判断方程组是否有解;根据二次型矩阵的特征值来判断二次型是否正定。以上都是根据它们的“量”来确定它们对应的“质”。在线性代数的学习中，要善于运用量变与质变的辩证关系。

案例6.在学习矩阵的可逆与不可逆、向量组的相关与不相关、方程组的有解和无解、方阵的可对角化与不可对角化时，教师可以引出“对立和统一”的辩证关系。

分析：線性代数的很多概念都是“对立和统一”相结合。因对立能由此知彼，因统一能互为利用，构成了线性代数丰富的知识体系。

案例7.在讲解易混淆的概念时，教师可以引出“现象与本质”的辩证关系。

分析：如在讲解行列式与矩阵的区别时，虽然其外表形状很相似，但其本质完全不同，行列式本质是一个值，而矩阵本质是一个数表;在讲解两个向量的乘积时，行向量左乘列向量与列向量左乘行向量，表面很相似，但前者是一个值，后者是一个方阵，完全不同。教师可以继续引入思政实例：比如两个学生博士毕业后，一个去华为工作，一个到外企工作，表面上看很类似，但本质相差甚大，培养学生“报效祖国，为国争光”的崇高思想。

案例8.在学习矩阵相似对角化时，教师可以引出“过程与结果”的辨证关系。

分析：矩阵相似对角化是线性代数一个重要知识点，其运算过程非常繁琐，同学们往往只重视其计算结果，而忽略了运算过程，但运算过程却是该知识点的核心。教师应该让学生明白奋斗的过程远比最终的结果重要，让学生学会如何面对成功与失败，学会实事求是的科学精神。

（五）从数学知识点出发，挖掘思政元素

从线性代数各章节具体知识点出发，深度挖掘各种思政元素。

案例9.在学习行列式和方阵的区别时，教师可以从细节出发，强调严谨求实的科学态度。

分析：行列式和方阵形式非常相似，一个用线段表示，一个用中（小）括号表示，初学同学非常容易混淆。作为教师要强调它们形式上和本质上的差异，不能原谅学生在细节上的错误，让学生最开始就建立一个“认真”、“严谨”的学习习惯，培养学生拥有一个严谨求实的科学态度。

案例10.在学习单位矩阵E时，教师可以根据单位矩阵运算特点引出积极的人生观等思政元素。

案例12.在学习用初等变换求逆矩阵时，教师可以引出“感恩”的思政元素。

分析：把“求矩阵的逆矩阵”类比为“寻找小时候的我”，用初等变换求逆矩阵是一个非常繁琐的计算过程，学生往往抱怨计算量太大，而且经常出错。教师可以通过这个例子引导学生理解父母是怎样把自己从小养大、艰辛教育、培养成才的过程，引出“要有一颗感恩的心”，“感恩父母”、“感恩学校”、“感恩国家”。

案例13.在学习向量的几何含义时，教师可以引出“树立人生目标”的思政元素。

分析：从向量的几何含义是一个有方向的线段出发，引导学生也应该有自己人生追求理想和目标，通过讲解“南辕北辙”寓言故事，教育学生要为祖国的繁荣强大而努力学习，建立正确价值观，提高自我管理能力。

案例14.在学习零向量时，引导学生“建立正确的价值观”。

分析：零向量0与非零向量α在一起，既可以理解为0与α平行，也可以理解为0与α垂直，零向量是没有方向的向量，教育学生不要做一个“没有理想和信念”的人，引导学生建立正确的世界观和价值观。

案例15.在学习向量组的极大无关组时，教师可以引出“为祖国争光”的思政元素。

分析：把一个人类比为一个向量，把建设祖国的各类人才类比为向量组的极大无关组，激发学生努力学习，刻苦研究，将来成为建设祖国的栋梁。

案例16.在学习向量空间定义时，教师可以引出“不忘初心，牢记使命”的思政元素。

分析：当向量集合满足向量加法和向量数乘的封闭性时，这个集合称为向量空间。教师可以把一组坚定的共产主义信仰者类比为一个向量集合，集合中任意一个人随着年龄增加，他的信仰不会变换（类比向量数乘）;集合中任意两个人培养出来的新人一定也是共产主义信仰者（类比向量加法），这样一组坚定的共产主义信仰者集合可以称为向量空间。教育学生一个人的信仰不应随时间的变化而发生变化，引出“不忘初心，牢记使命”，为中国的繁荣强盛而努力奋斗。

五、结语

全面实施课程思政，已成为中国高等教育界的共识。有效实现课程思政，需要学校做好顶层设计。西安电子科技大学以文件的形式给出了实施意见，并于11月初开展了全校范围内的课程思政教学比赛，西安电子科技大学线性代数教学团队获得一等奖，我们将进一步按照教育部和学校的文件精神努力把课程思政做好做精，真正做到春风化雨、润物无声，把正确的世界观、价值观潜移默化地沁入学生的心田，把线性代数课程培育成思政示范课，以此带动其他课程思政和专业思政建设。

[责任编辑：林志恒]