中考中和字母系数有关的分类讨论型问题

刘 莉

(湖北省钟祥市长寿路学校 431900)

一、方程与函数概念的讨论

1.已知关于x的方程(m2-4)x2+(m-2)x+3m=0，当m____时，它是一元二次方程；当m____时，它是一元一次方程. (m≠±2;m=-2)

2.已知y=(m-4)xm(m-1)+2x2-3x-1

(1)当m为何值时，它是y关于x的一次函数；

(2)当m为何值时，它是y关于x的二次函数.

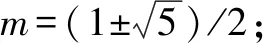
二、方程的解的情况与交点个数的讨论

1.阅读下面的材料，并解答后面的问题

材料：试探讨方程ax=b的解的情况．

当a≠0时，方程有唯一解x=b/a；

当a=b=0时，方程有无数解；

当a=0，b≠0时，方程无解．

问题：已知关于x的方程a(2x-1)=3x-2，请你讨论它的解的情况．

分析首先把方程化成一般形式，然后对一次项系数进行讨论即可．

解答原式即(2a-3)x=a-2，当2a-3≠0，即a≠3/2时，方程的解是x=(a-2)/(2a-3)；

当2a-3=0,即a=3/2时，此时a-2≠0，方程无解．

点评本题考查了方程的解，正确对方程进行化简是关键.

2.(2014荆门)已知：函数y=ax2-(3a+1)x+2a+1(a为常数).

(1)若函数图象与坐标轴只有两个交点，求a的值.(2)略

解析①当a=0时,y=-x+1,有两个交点(0，1)，(1，0)；②当a≠0且图象过原点时，2a+1=0,a=-1/2,有两个交点(0，0)，(1，0)；③当a≠0且函数图象与x轴只有一个交点时，令y=0,则一元二次方程ax2-(3a+1)x+2a+1=0的判别式Δ=(3a+1)2-4a(2a+1)=0,解得a=-1，有两个交点(0，-1)，(1，0).综上得：当a=0或-1/2或-1时，函数图象与坐标轴有两个交点.

三、方案讨论

1.(2018东湖高新)某公司有A型产品40件，B型产品60件，分配给下属甲、乙两个商店销售，其中70件给甲店，30件给乙店，且都能卖完.两商店销售这两种产品每件的利润(元)如下表：

A型产品利润(元/件)B型产品利润(元/件)甲店200170乙店160150

设分配给甲店A型产品x件，公司卖出这100件产品的总利润为w元.

(1) 请你求出w与x的函数关系式；

(2) 请你帮公司设计一种产品分配方案使总利润最大，最大总利润是多少元？

(3) 为了促销，公司决定只对甲店A型产品让利a元/件，单让利后仍高于甲店B型产品每件利润，请问x为何值时，总利润最大？

解析(1)w=20x+16800.(2)略.

(3) 依题意得：0≤a<30,w=(200-a)x+160(40-x)+170(70-x)+150(x-10)=(20-a)x+16800(10≤x≤40).当0≤a<20,即20-a>0时，w随x增大而增大，所以x=40，总利润最大；当a=20，即20-a=0时，10≤x≤40,即符合题意的各种方案，总利润都一样大；当20

2.(2017年武汉武昌区五调)荆楚商厦购进和销售A,B两种商品，A,B两种商品的进价和售价如下表：

商品进价(元/件)售价(元/件)A2024B16a(16

根据表中信息，解答下列问题：

(1)如果用960元购进A,B两种商品共50件，求购进A,B商品各多少件？

(2)如果购进这两种商品50件且全部售完，求获取利润的最大值.

解析(1)购进A商品40件，B商品10件.

(2)设购进A商品x件，利润为W元，则购进B商品(50-x)件，则W=(24-20)x+(a-16)(50-x)=(20-a)x+50(a-16).当16

练习：(1)关于x的方程(k-1)x2+4x+1=0有实数根，则k的取值范围是____.

(2)关于x的一元一次方程(k2-1)xk-1+(k-1)x-8=0的解是____.

(3)若函数y=ax2-ax+3x+1的图象与x轴只有一个交点，求a值与交点坐标.

(4)A城有某种农机30台，B城有该农机40台，现将这些农机全部运往C,D两乡，调运任务承包给某运输公司.已知C乡需要农机34台，D乡需要农机36台.从A城往C,D两乡运送农机的费用分别为250元/台和200元/台，从B城往C,D两乡运送农机的费用分别为150元/台和240元/台.

(1)设A城运往C乡该农机x台，运送全部农机的总费用为W元，求W关于x的函数关系式，并写出自变量x的取值范围；

(2)现该运输公司对A城运往C乡的农机，从运输费中每台减免a元(a≤200)作为优惠，其他费用不变,如何调运，使总费用最少？