重视运用对称 解决代数问题

杨红余

(甘肃省平凉市第四中学 744000)

数学中蕴含大量的对称思想，借助对称思想，利用对称的特性，可以实现初中数学中较典型的问题的求解.针对涉及到对称的问题，要对问题的关键字眼保持一定的敏感性，如题目中包含存在关系、逻辑关系，尤其是位置关系的对称时，就可以优先考虑利用对称解决问题.

一、利用对称性，求解函数最值问题

函数最值的求解方法比较多，可借助具体的数值来确定最值大小，也可以借助有关函数图形进行考虑.每种方法有其使用的范围，当问题出现两个甚至多个代数和是一个定值，求解满足一定关系式的函数值时，可以考虑从对称的角度去解决.

例1已知a>0,b>0，且z=ab，若a+b=2时，求z的最大值.

解析观察发现a+b=2，即意味着a,b的和是个定值，因此当a越大时，对应的b就越小；a越小时，相对应的b的取值就越大.若是a,b两个取值相等，则意味着a,b在关系上是相互对称的.因此，可以巧妙借助a,b这种相互对称的关系，可以令a=1-r,b=1+r，此时始终满足a+b=2的条件.最后，z=ab就等价转化为z=(1-r)(1+r)=1-r2.由于r2永远是不小于0的，所以只有r=0时，z能够取到最大值，是1.具体解题如下：设a=1-r,b=1+r，则z=ab=(1-r)(1+r)=1-r2，又r2≥0，所以z=1-0=1，即z的最大值是1.

反思此题借助对称性，将a,b用特殊的式子进行表示，实现问题的简化.若采用常规的方法用b=2-a进行表示，并代入z=ab中，结合自变量a>0以及二次函数的性质也能求解.但有些同学会将z=-a2+2a开口方向弄错，进而造成结果的错误.如果问题变成a,b,c,d均大于0，且a+b+c+d=2，求z=abcd的最大值时，利用对称性解题就比较简单.

二、依靠对称性，判断函数值的大小

有关两个函数值的大小，常常是将两个函数值求出来，然后再断大小；也可以借助图象进行辅助.但是，当函数值不便求解，甚至无法根据已知条件求出具体值时，不妨借助函数的对称性质，进行综合考虑.

反思借助对称判断点关于对称轴的位置关系，然后借助位置判断大小，不过还需要掌握函数y=x2-3x-2的图象开口方向，然后才能借助距离判断函数值大小.

三、运用对称性，证明不等式

在许多代数问题中都包含对称思想，从对称角度出发，借助对称的有关性质，可以降低不等式的证明难度.

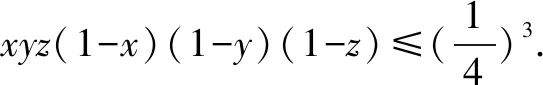
综上所述，在某些具有对称性的代数问题中，巧妙地运用对称性，把握对称的特质，往往能够使得问题求解过程变得简洁明了，实现解决问题方法与思路的优化.