单轴压缩下Ti3B4的力学、电学性能及变形机制的第一性原理研究*

李君 刘立胜 徐爽 † 张金咏

1) (武汉理工大学, 新材料力学理论与应用湖北省重点实验室, 武汉 430070)

2) (武汉理工大学, 材料复合新技术国家重点实验室, 武汉 430070)

3) (武汉理工大学, 先进材料制造装备与技术研究院, 武汉 430070)

Ti3B4作为一种重要的钛硼化合物, 被广泛应用于工业生产和国防军事中.但是有关Ti3B4在外载荷下的变形行为却鲜有报道, 这在很大程度上限制了它的应用.本文采用基于密度泛函理论的第一性原理方法研究了Ti3B4在不同方向单轴压缩下的力学行为、电子结构以及变形机制.结果表明, 在不同方向单轴压缩下,Ti3B4的变形行为表现出很强的各向异性.a轴压缩下, 层内Ti− Ti键减弱使Ti3B4承载能力降低, 最终层间Ti−Ti键和沿b轴B−B键断裂造成压缩应力突降; b轴压缩下, 层内Ti−B键减弱和层间Ti−B键增强导致Ti3B4承载能力逐渐降低, B−B键断裂导致结构破坏; c轴压缩下, 层内Ti−B键断裂和层间Ti−B键形成使结构稳定性降低.由态密度分布可知, 在单轴压缩下, 变形后的Ti3B4仍然呈现金属性, 但是其共价性能降低.通过讨论Ti3B4在不同方向单轴压缩下的力学行为与微观变形机制可以为改善其宏观性能提供一定的理论指导.

1 引 言

硼化钛是一类典型的类金属陶瓷化合物, 具有高熔点、高硬度、良好的导电性以及低电阻率等优点, 被广泛地用于制作高温坩埚、切削刀具等, 同时又是良好的电极材料以及装甲防护材料等[1—3].在钛硼化合物中, 人们已经证明存在三种稳定的结构: TiB2, Ti3B4和TiB[4,5], 其中由于TiB2具有高弹性模量 (E = 565 GPa)、高硬度 (Hv = 25 GPa)、优良的耐磨性和导电性[2], 因此迄今为止, 有大量科研人员利用试验方法或者计算手段对TiB2的基本材料性质和力学行为进行了研究[6−22].对于TiB, 由于其具有良好的微观结构和力学性能, 被广泛地用作金属基复合材料的增强体[23,24], 因此在近年来也备受关注[8—11,25,26].然而对于Ti3B4, 作为钛硼化合物的中间相, 虽然其强度和硬度介于TiB2和TiB之间, 被广泛用于工业生产和军事防护中[10,11,27], 但是有关其力学行为, 尤其是在外载荷下的变形行为却鲜有报道.

目前, 一些研究人员分析了Ti3B4的基本材料性质, 包括弹性性质、电子结构和热力学特性等,发现Ti3B4的弹性模量和硬度仅次于TiB2, 而高于TiB[10,11,27].接着, 他们进一步研究了静水压力和温度等因素对Ti3B4的力学、热力学性质以及变形行为的影响[10,11,28].研究表明, 随着静水压力增加, Ti3B4的弹性模量、体积模量、各向异性以及德拜温度都随之增加且几乎线性变化, 但是电子结构却没有显著改变.值得注意的是, 在静水压力下,与TiB2和TiB类似, Ti3B4结构一直保持稳定, 没有发生结构相变或者破坏.然而, 作为一种工业类金属陶瓷, 在实际应用中, 钛硼化合物常常处于非常复杂的应力状态, 因此研究非静水压力条件下钛硼化合物的变形行为及内在机制尤为重要.

众所周知, 密度泛函理论(density functional theory, DFT)是计算材料物理性质以及变形机理的最精确的方法之一[10−14,27—35].基于此, 少数研究人员利用基于DFT的第一性原理方法分析了TiB2和TiB在单轴载荷和剪切载荷下的变形行为[12—14].Zhang 等[12]计算了 TiB2, ZrB2和 HfB2的拉伸强度和剪切强度, 结果表明TiB2在(0001)滑移面的剪切强度最弱.Cheng和Li[13]分析了温度对TiB2, ZrB2和HfB2拉伸强度的影响, 发现随着温度增加, 其拉伸强度在初始阶段几乎保持不变, 随后线性降低, 与弹性模量的变化类似.Sun等[14]分析了TiB2在单轴载荷下的变形行为并讨论了其各向异性, 结果表明TiB2的压缩强度要远高于拉伸强度, 同时反键态的出现是导致TiB2结构稳定性降低的主要原因.Li等[29]通过分析TiB在不同方向单轴压缩载荷下的变形行为,重点讨论了TiB的各向异性.而对于Ti3B4, 人们对其在外载荷下, 尤其是非静水压力下的力学行为和变形机制的认识仍然有限.因此, 开展相关研究工作十分必要.

本文采用基于DFT的第一性原理方法, 研究了Ti3B4在不同方向单轴压缩下的力学行为、电子结构以及变形机制, 重点比较讨论了Ti3B4的各向异性行为.深入分析Ti3B4结构在外载荷下的微观变形机理, 对于提高其宏观力学性能, 以及设计合成具有优良特性的钛硼复合材料具有一定的指导意义.

2 计算方法及模型

Ti3B4晶体属于正交晶系, 空间群为 71(Immm), 利用X射线粉末衍射试验可以确定其晶格常数a0= 3.259 Å, b0= 13.73 Å, c0= 3.032 Å[5],其中6个钛(Ti)原子和8个硼(B)原子分别占据Ti(1) (0.5, 0.5, 0), Ti(2) (0, 0.18, 0)和B(1) (0,0.375, 0), B(2) (0, 0.444, 0.5)格位.Ti3B4的晶体结构如图1所示.图1(a)为Ti3B4的单胞结构, 可以看出Ti3B4是由两种不同的层状子结构组成的共生结构, 其中一层为B原子组成的六边形子结构, 另一层为Ti原子组成的子结构.Ti3B4的超胞结构如图1(b)所示, 其中B原子组成的六边形结构沿着c轴方向重复排列.Ti3B4的化学键可以分为几类[28]: 1) 沿b轴方向的B−B键, 即B1—B2键;2) 偏离b轴的B—B键, 即B1—B3键; 3) 层内的Ti—Ti键, 即Ti1—Ti2键, 该化学键与b轴夹角约为 30°; 4) 层间的 Ti—Ti键, 即 Ti1—Ti3键;5) 层内的 Ti—B键, 即 Ti1—B1键和 Ti1—B3键等[17,26,28].

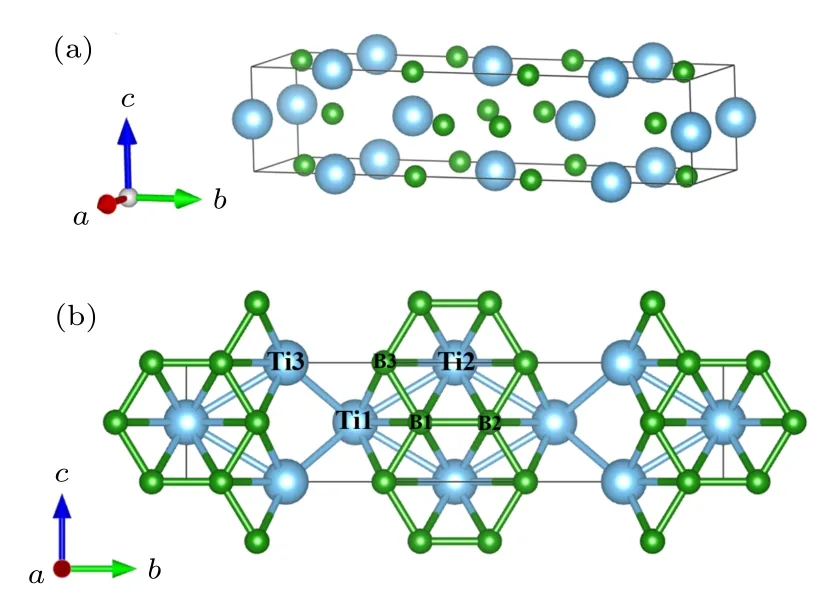
图1 Ti3B4的晶体结构 (a) 单晶胞结构; (b) 超晶胞结构.其中蓝色原子为Ti原子, 绿色原子为B原子Fig.1.The crystal structure of Ti3B4: (a) The unit cell;(b) the supercell.The blue balls in the figure denote the Ti atoms, and the green balls refer to the B atoms.

本 文 采 用 基 于 DFT的 Vienna ab−initio simulation package (VASP)[36—38]进行了第一性原理计算.选取了广义梯度近似 (generalized gradient approximation, GGA) 作为交换关联函数, 投影缀加波 (projected augmented wave,PAW) 作为赝势来描述离子实和价电子之间的相互作用, 其中Ti原子和B原子的价电子构型分别为3s23p63d24s2和2s22p1.为了同时保证计算效率和准确性, 首先利用上述Ti3B4的试验晶格常数[5]进行了收敛性测试, 确定k点网格为13 × 3 ×13, 平面波截断能为600 eV.在结构优化过程中,Ti3B4的原子位置、晶胞体积以及晶胞形状都得到了充分弛豫.优化后Ti3B4的晶格常数为a0=3.255 Å, b0= 13.729 Å, c0= 3.035 Å, 其原子键长度为: 1) 沿b轴方向的B—B键长为1.767 Å;2) 偏离b轴的B—B键长为1.777 Å; 3) 层内的Ti−Ti键 长 为 2.962 Å; 4) 层 间 的 Ti−Ti键 长 为2.848 Å; 5) 层内的 Ti−B 键的平均长度为 2.374 Å,与前人的计算结果保持一致[10,11,28].

为了研究Ti3B4在非静水压力下的变形行为,本文基于优化后的Ti3B4晶体结构, 分别沿着a轴、b轴和c轴施加了单轴压缩应变, 其中应变增量为1%.在每个应变水平下, 除加载方向外, 其余五个应力分量完全弛豫, 并且将弛豫后应力大小控制在0.1 GPa以下.此外, 为了保证加载的连续性与准确性, 在加载过程中, 需将前一步优化弛豫后的晶体结构作为下一步加载的初始结构.

3 计算结果分析与讨论

3.1 应力-应变曲线

图2所示为Ti3B4在单轴压缩下的应力−应变曲线.在a轴压缩下, 当压缩应变小于0.14时, 压缩应力几乎线性增加.接着, 压缩应力单调增加到最大值77.9 GPa (ε = 0.24), 但是增加速率明显减小.当压缩应变ε = 0.25时, 压缩应力突降至19.0 GPa.为了详细分析Ti3B4在该突变点附近的变形行为, 在压缩应变ε = 0.24—0.25之间以0.2%作为应变增量进行了加载.结果表明, 压缩应力在ε = 0.242时突降至最小值16.6 GPa, 说明此时结构发生破坏.当沿着b轴加载时, 压缩应力首先几乎线性增加至82.97 GPa (ε = 0.13).然后随着压缩应变增加, 压缩应力虽然单调增加至最大值97.0 GPa (ε = 0.19), 但是其增加速率明显减小.接着, 压缩应力依旧保持连续变化但是开始下降, 表明结构虽然开始发生破坏但仍然可以继续承载.当压缩应变ε = 0.268时, 压缩应力从78.2 GPa突降至30.5 GPa, 表明结构完全破坏.在c轴压缩下, 当压缩应变小于0.12时, 应力几乎线性增加.然后压缩应力发生小幅波动并在ε =0.15时达到最大值82.2 GPa, 此时结构稳定性降低.随着压缩应变进一步增加, Ti3B4结构处于不稳定状态, 承载能力逐渐降低.

以上结果表明, Ti3B4在a轴、b轴和c轴单轴压缩下的最大应力分别为77.9, 97.0和82.2 GPa,说明Ti3B4在b轴方向的抗压能力最强.与试验结果相比[27], 本文计算得到的压缩应力值要大得多,这主要有两个原因: 1)本文计算所采用的模型为完美的Ti3B4单晶, 忽略了空位和位错等缺陷的影响, 而这在试验中几乎是不可能实现的; 2)第一性原理计算是在绝热环境下进行的, 而实验通常是在室温条件下.由图2可以看出, 在单轴压缩下,Ti3B4的力学行为发生了显著的改变, 并且当沿着不同方向加载时, 它的变形行为也不尽相同, 反映出Ti3B4晶体具有很强的各向异性.为了深入分析Ti3B4在单轴压缩下的力学行为和变形机制, 本文利用电子局域函数 (electron localization function, ELF)[39,40]进一步研究了Ti3B4的微观结构变化.ELF可以用来表征电子的局域化分布特征, 其优点是无需计算局域分子轨道, 计算量相对较小.

图2 Ti3B4晶体在单轴压缩载荷下的应力−应变曲线Fig.2.The stress−strain relationship of Ti3B4 under uniaxi−al compressions.

3.2 微观结构变化

1) a轴单轴压缩

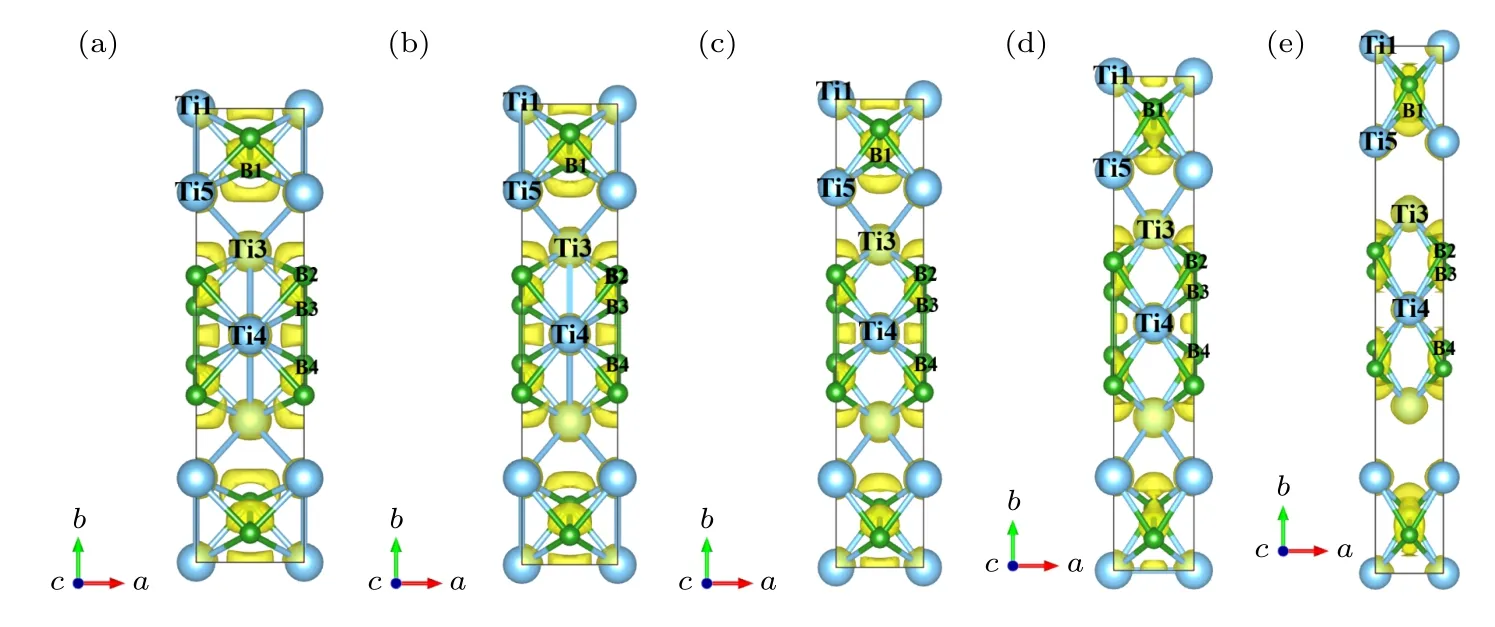
图3 a 轴压缩时不同应变下 Ti3B4晶体的结构和 ELF 分布图 (a) ε = 0.00; (b) ε = 0.10; (c) ε = 0.15; (d) ε = 0.24; (e) ε = 0.242Fig.3.The structural and ELF at various strains under a−axis uniaxial compression: (a) ε = 0.00; (b) ε = 0.10; (c) ε = 0.15; (d) ε =0.24; (e) ε = 0.242.

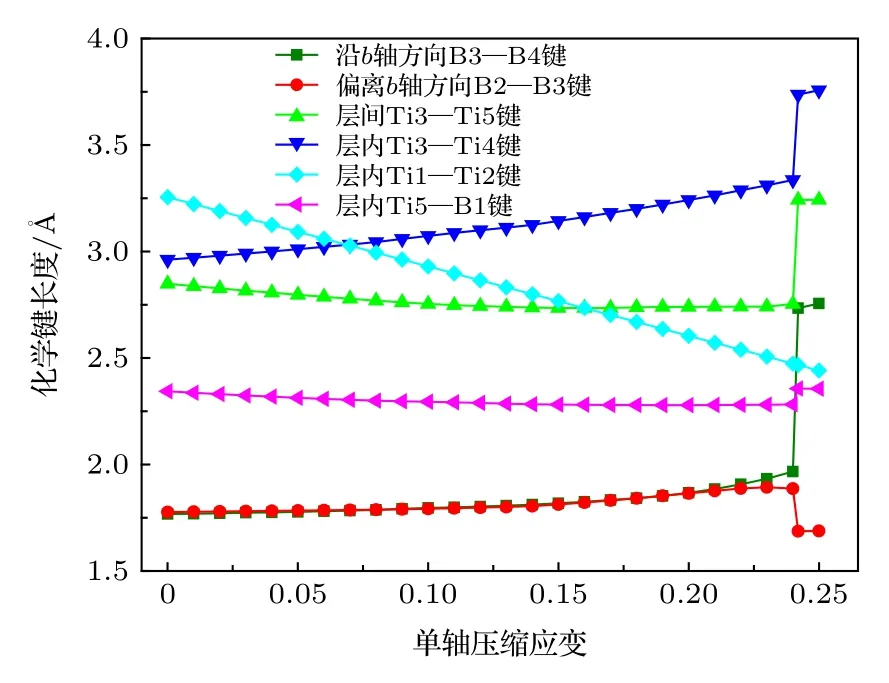
图4 Ti3B4晶体在a轴压缩下化学键长度变化Fig.4.Variation of bond lengths as a function of a−axis uni−axial compressive strain.

Ti3B4在a轴压缩下的结构和ELF分布变化情况如图3所示.图3(a)所示为Ti3B4的初始结构.随着压缩应变增加, Ti3B4发生均匀变形, 导致压缩应力几乎线性增加(见图2), 说明此时结构处于弹性变形阶段, 结构与ELF分布图变化不明显,如图3(b)所示.然而, 随着压缩应变增加, 层内Ti3—Ti4键长度也逐渐增大, 表明层内Ti3−Ti4原子间相互作用逐渐减弱甚至可以忽略(见图4).在此过程中, Ti3B4结构发生了一定程度的扭曲, 如图3(c)所示.虽然Ti3B4仍然可以继续承载, 但是承载能力降低, 导致后续压缩应力虽仍然保持单调递增但增加速率明显降低(见图2).当压缩应变增加到0.24时 (见图3(d)), 结构依然保持亚稳定状态, 此时压缩应力达到最大值77.9 GPa.当压缩应变ε = 0.242时, 如图4所示, 层间Ti—Ti键和沿b 轴方向 B—B键长度突然增大，其中层间Ti3—Ti5键长度由 2.75Å (ε = 0.24)突然增大至3.24Å, 表明 Ti3—Ti5键断裂.为了进一步说明B—B键的变化,图5给出了Ti3B4在(100)晶面上的 ELF图, 其中数值表示 ELF值, 可以发现B—B键的 ELF值由 0.79(ε = 0.24)突降为0.46(ε = 0.242), 表明沿b轴方向B—B共价键发生断裂.层间Ti—Ti键和沿b轴方向B—B键的断裂(见图3(e))使Ti3B4完全破坏, 无法继续承载, 导致压缩应力突然下降至16.61 GPa.

2) b轴单轴压缩

图5 a轴压缩时临界应变下Ti3B4晶体(100)晶面ELF 分布图 (a) ε = 0.24; (b) ε = 0.242Fig.5.The ELF at critical strains of (100) crystal plane in Ti3B4 structure under a−axis uniaxial compression: (a) ε =0.24; (b) ε = 0.242.

图6所示为Ti3B4在b轴压缩下的结构和ELF分布变化图.当压缩应变小于0.13时(见图6(a)),Ti3B4晶体结构保持完整并均匀变形, 表明其处于弹性变形阶段.接着, 随着压缩应变增加, Ti3B4结构原子间化学键发生变化, 导致结构逐步发生扭曲.如图7所示, 层间Ti2—B3键长度逐渐减小,而层内Ti1—B1键长度则逐渐增加, 表明层间Ti—B化学键逐渐增强, 而层内Ti−B原子间相互作用逐渐减弱直至可以忽略.[,,28]为了清楚说明Ti−B原子间相互作用, 本文同时考虑了 Ti−B的Mulliken布居[41].Mulliken布居可以用来表示电荷在各组成原子之间的分布情况, 正值表示为成键态, 负值表示为反键态.同时数值的大小可以表示化学键的共价性质和离子性质, 数值为0表示为纯离子键, 数值为1表示为纯共价键, 数值越大表明该化学键的共价性越强[41].当ε = 0.10时, 层内Ti1−B1键和层间Ti2—B3键的Mulliken布居值分别为0.35和—0.17.当压缩应变增加至0.26时,它们的Mulliken布居值变化为—0.10和0.08, 表明在此过程中, 层内Ti1—B1键断裂, 形成了新的层间Ti2—B3键, 如图6(b)和图6(c)所示.同时沿b轴方向B—B键的ELF值逐渐减小, 表明B−B原子间相互作用也在逐渐减弱, 如图8所示.在此过程中, 虽然Ti3B4仍然可以继续承载, 使压缩应力在ε = 0.19时达到最大值97.0 GPa.但是其承载能力逐渐降低, 导致后续压缩应力连续下降(见图2).当 ε = 0.268 时 (见图6(d)), Ti3B4结构已经完全破坏, 尤其是沿b轴方向B—B键的断裂(见图8(d))导致Ti3B4无法继续承载, 使压缩应力从78.2 GPa突降至30.5 GPa.

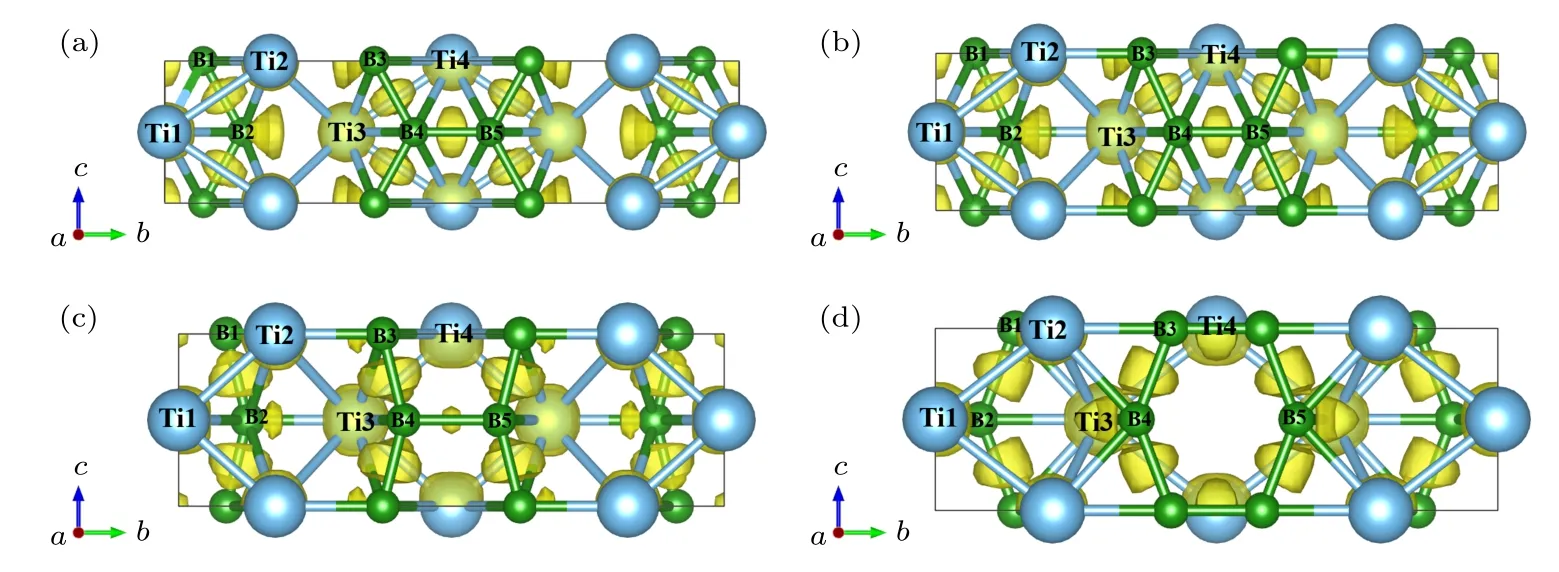
图6 b轴压缩时不同应变下Ti3B4晶体的结构和ELF分布图 (a) ε = 0.10; (b) ε = 0.14; (c)ε = 0.26; (d) ε = 0.268Fig.6.The structural and ELF at various strains under b−axis uniaxial compression: (a) ε = 0.10; (b) ε = 0.14; (c) ε = 0.26; (d) ε =0.268.

图7 Ti3B4晶体在b轴压缩下化学键长度变化Fig.7.Variation of bond lengths as a function of b−axis uni−axial compressive strain.

3) c轴单轴压缩

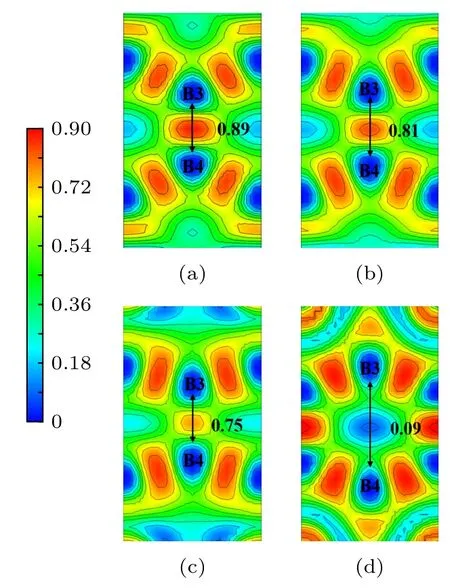
图8 b轴压缩时临界应变下Ti3B4晶体(100)晶面ELF 分布图 (a) ε = 0.14; (b) ε = 0.20; (c) ε = 0.26; (d) ε =0.268Fig.8.The ELF at critical strains of (100) crystal plane in Ti3B4 structure under b−axis uniaxial compression: (a) ε =0.14; (b) ε = 0.20; (c) ε = 0.26; (d) ε = 0.268.

图9所示为Ti3B4在c轴压缩下的结构和ELF分布变化情况.当压缩应变小于0.12时, 如图9(a)所示, Ti3B4均匀变形, 表明该结构处于弹性变形阶段, 且原子间化学键长度变化较小(见图10).然后, 随着压缩应变增加, 如图10所示, 层内Ti—B键(Ti1—B2键和Ti2—B1键)长度迅速增大, 说明层内Ti—B化学键强度急剧降低, 而层间 Ti2−B3原子间相互作用却在快速增强.Ti3B4结构中Ti−B原子间相互作用的快速改变(见图9(b)和图9(c))导致它的压缩应力出现小幅度波动, 但此时结构仍然处于相对稳定状态.接着,当压缩应变达到 0.20时, 层内 Ti1—B2键和Ti2—B1键以及层间Ti2—B3键的Mulliken布居值分别为—0.22, —0.57和 0.22, 表明层内 Ti−B 原子间相互作用可以忽略, 同时形成了新的层间Ti−B键(见图9(d)和图9(e)), 从而导致Ti3B4结构处于不稳定状态, 承载能力降低, 造成压缩应力出现较大波动并逐步减小.

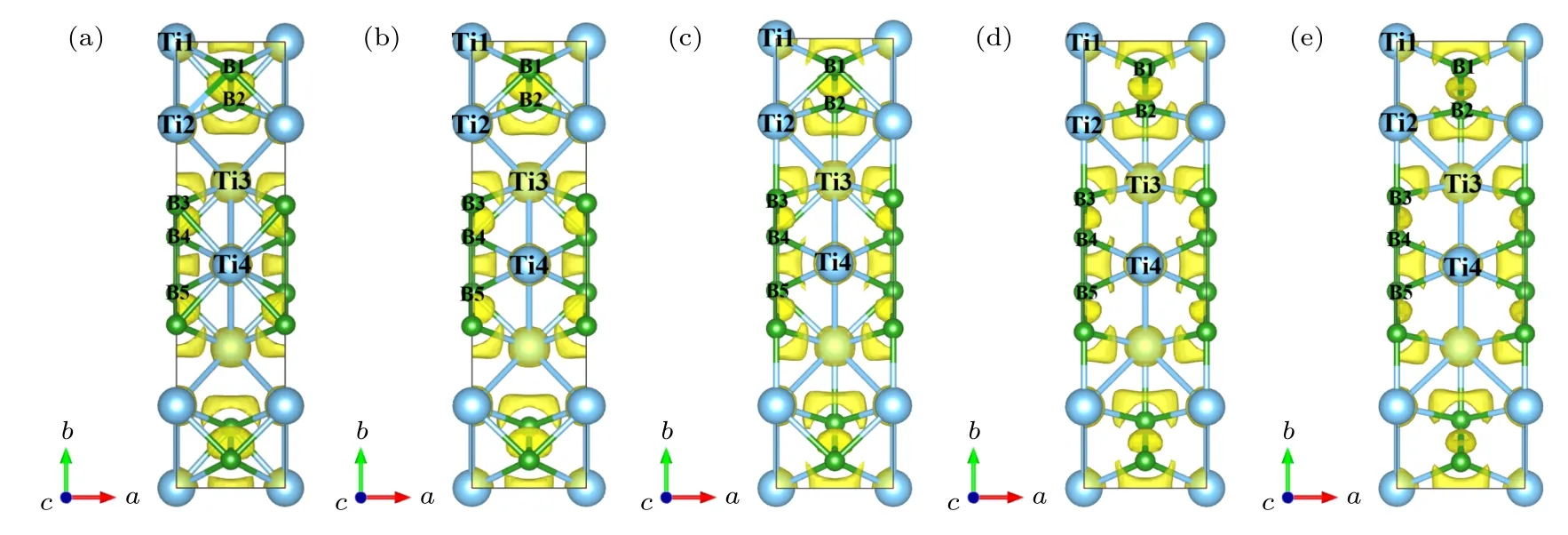
图9 c 轴压缩时不同应变下 Ti3B4晶体的结构和 ELF 分布图 (a) ε = 0.10; (b) ε = 0.13; (c) ε = 0.18; (d) ε = 0.20; (e) ε = 0.26Fig.9.The structural and ELF at various strains under c−axis uniaxial compression: (a) ε = 0.10; (b) ε = 0.13; (c) ε = 0.18; (d) ε =0.20; (e) ε = 0.26.

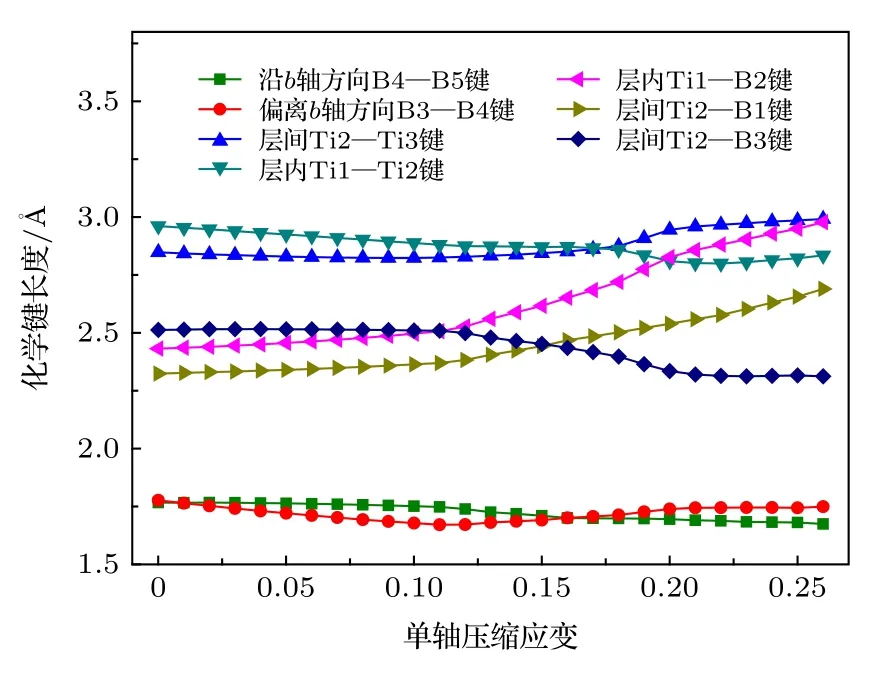
图10 Ti3B4晶体在c轴压缩下化学键长度变化Fig.10.Variation of bond lengths in Ti3B4 as a function of c−axis uniaxial compressive strain.

Ti3B4, TiB2和TiB是一类典型的类金属陶瓷化合物, 其中Ti3B4的强度和硬度介于TiB2和TiB 之间, 即: TiB2＞ Ti3B4＞ TiB.在静水压力下, TiB2, Ti3B4和TiB结构都始终保持稳定, 没有发生结构相变或者破坏[10].但是在非静水压力下, TiB2, Ti3B4和TiB都会发生破坏, 且它们的变形机制各不相同.本文重点讨论的是Ti3B4在不同方向单轴压缩下的力学行为和变形机理, 而Sun等[14]和本课题组[29]分别研究了TiB2和TiB在不同方向单轴载荷下的破坏行为.Sun等[14]将TiB2结构的破坏归因于反键态的出现.而对于TiB, 本课题组前期发现当沿着不同方向加载时,TiB的力学行为同样会表现出明显的各向异性[29].当沿着 a轴加载时, Ti—Ti键的变化, 即Ti1—Ti3键断裂同时形成新的Ti1—Ti4键, 是TiB的主要变形机制; 当沿着b轴加载时, TiB的变形行为主要与Ti−B原子间相互作用有关.首先Ti1—B1键的断裂和 Ti3—B3键的形成导致TiB结构发生扭曲, 造成应力波动.最后TiB结构中重新形成新的Ti1—B1键, 导致结构发生破坏;当沿着c轴加载时, 沿着b方向B—B键的断裂是导致结构破坏的主要原因.

3.3 电子态密度

为了进一步研究单轴压缩载荷对Ti3B4基本材料性质的影响, 本文分别分析了它在a轴、b轴和c轴压缩下的态密度(density of states,DOS)分布.DOS分布不仅可以用于研究晶体的电子结构和化学键特性, 而且也是判断结构导电性能的一个重要因素.由于原子间的成键情况主要由费米能级周围的DOS表现, 因此本文重点分析了[—13, 7]eV范围之间的DOS分布, 包括总态密度(total density of states, TDOS)和分波态密度(partial density of states, PDOS).图11所示为Ti3B4初始结构的TDOS和PDOS, 其中能量零点处的垂线代表费米能级EF.由于费米能级处的DOS值不为零且其附近没有能量间隙, 说明Ti3B4表现为金属性, 进一步说明钛硼化合物均为类金属导电陶瓷[14,29].由图11可以看出, 能量在[—12, —4]eV 范围内的 DOS主要由 B−2s和 B−2p轨道组成; 能量在[—3, 0]eV范围内, 即费米能级附近, 价带顶部的DOS主要由Ti−3d和B−2p轨道杂化形成; 而在导带底部, DOS主要由Ti−3d轨道组成.同时在费米能级右侧, 即能量为0.98 eV处存在赝能隙(DOS曲线中费米能级附近两峰之间的间距[42,43]).

图11 Ti3B4初始结构的TDOS和PDOS分布Fig.11.TDOS and PDOS for undeformed Ti3B4.

表1 峰值A和谷值B处的Ti原子和B原子的PDOS和Ti3B4的TDOS (states/eV)Table 1.The PDOS of a Ti and a B atom and TDOS of Ti3B4 at Peak A and Bottom B (states/eV).

为了定量说明每个原子对Ti3B4的TDOS的贡献, 表1列出了Ti原子和B原子的各个轨道对图11所示的峰值A和谷值B处TDOS的贡献.对于峰值 A, 显然 Ti−3d (0.561 states/eV) 和 B−2p(0.527 states/eV)为主要贡献者.由于Ti3B4单胞中有6个Ti原子和8个B原子, 因此可以得出Ti−3d轨道和 B−2p轨道对峰值 A处 TDOS的贡献分别为25.7%和 32.2%.由于Ti−3d轨道和B−2p轨道的贡献相近, 说明Ti3B4中的共价键主要是由Ti−3d轨道和B−2p轨道杂化形成的, 这与TiB2结构和TiB结构十分类似[7,26].然而, 对于谷值B, Ti−3d轨道(0.20 states/eV)为主要贡献者,所占百分比为52.9%.因此在Ti3B4中, 其赝能隙是由Ti−3d轨道独自形成的, 这与TiB结构类似[29].然而, 与Ti3B4和TiB不同, TiB2的赝能隙是由 Ti−3d轨道和 B−2p轨道杂化形成的[17,18].

如图2所示, Ti3B4的临界压缩应变分别为ε =0.242 (a轴), ε = 0.268 (b轴)和 ε = 0.19 (c轴).如上所述, Ti3B4结构在临界压缩应变处发生了很大的改变, 因此相应的TDOS和PDOS分布也会有显著变化, 如图12所示.与初始结构类似, 变形后的Ti3B4仍然呈现金属性.同时在低能区域, 变形后的Ti3B4的TDOS主要由B−2s和B−2p轨道组成.而在费米能级附近, 其TDOS主要由Ti−3d和B−2p轨道杂化形成.然而, 由图12(a)和图12(b)可以看出, 在a轴和b轴压缩下, 变形后的Ti3B4没有明显的赝能隙.但是当沿着c轴加载时, 变形后的Ti3B4中仍然存在赝能隙, 但是向低能方向移动, 从0.98 eV移动至0.58 eV.同时赝能隙宽度变窄, 表明此时Ti3B4的共价性能降低.

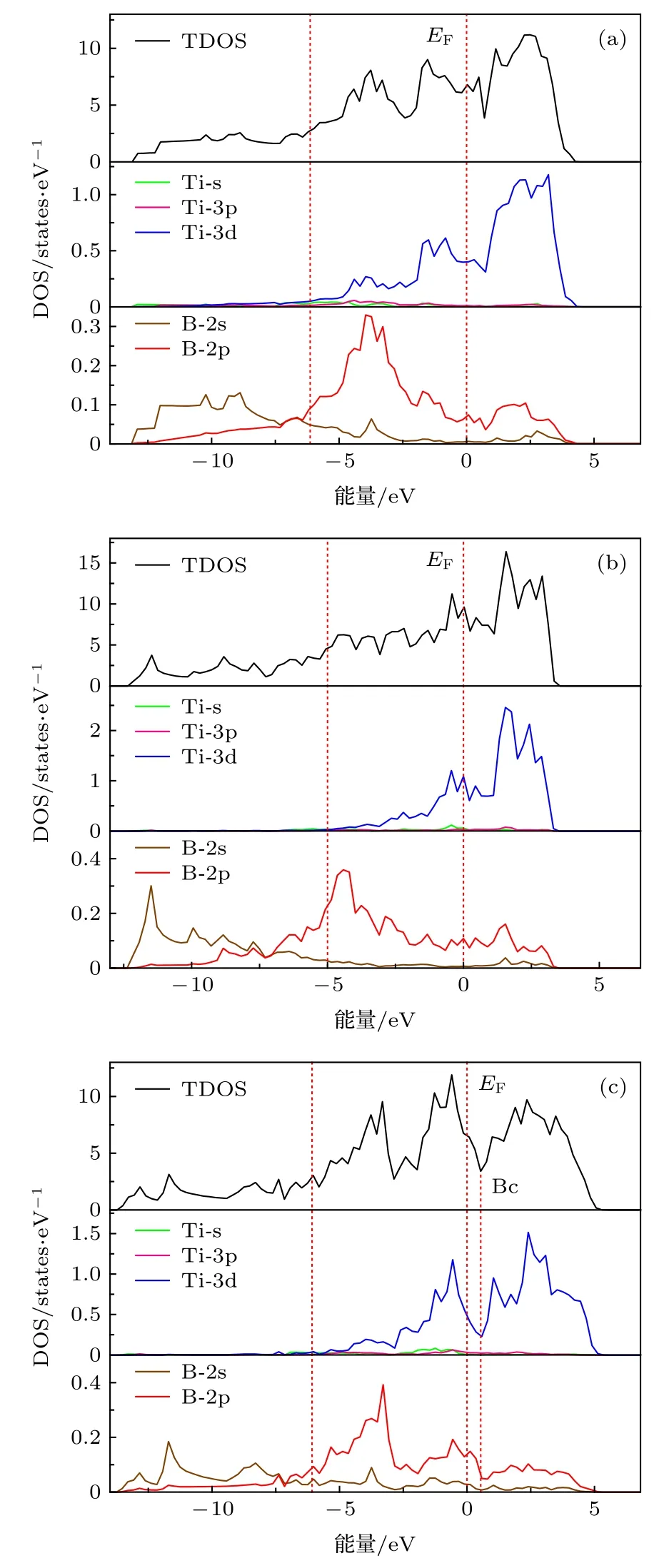
图12 在单轴压缩下Ti3B4结构在临界压缩应变处的TDOS 和 PDOS 分布 (a) ε = 0.242 (a轴); (b) ε = 0.268(b轴); (c) ε = 0.19 (c轴)Fig.12.TDOS and PDOS for Ti3B4 at critical strains un−der uniaxial compressions: (a) ε = 0.242 (a−axis); (b) ε =0.268 (b−axis); (c) ε = 0.19 (c−axis).

通过DOS分布可知, TiB2, Ti3B4和TiB的初始结构均呈现金属性[14,29], 进一步说明钛硼化合物为类金属导电陶瓷.在低能区域, 它们的DOS主要由B−2s和B−2p轨道组成; 在费米能级附近,它们的DOS主要由Ti−3d和B−2p轨道杂化形成.同时在费米能级附近, TiB2, Ti3B4和TiB均存在赝能隙, 但是Ti3B4和TiB[29]的赝能隙主要由Ti−3d轨道独自形成, 而 TiB2的赝能隙主要由Ti−3d轨道和B−2p轨道杂化形成[17,18].在单轴压缩下,变形后的钛硼化合物仍然呈现金属性[14,29], 但是部分破坏后的结构没有明显的赝能隙.即使有赝能隙存在, 其宽度也会变窄并向低能方向移动, 表明破坏后的钛硼化合物的共价性降低.

4 结 论

本文采用基于密度泛函理论的第一性原理方法研究了Ti3B4在不同方向单轴压缩载荷下的力学行为、电子结构和变形机制.结果表明,Ti3B4在a轴、b轴和c轴压缩下的最大应力分别为77.9, 97.0和82.2 GPa, 说明Ti3B4在b轴方向的抗压能力最强.

在不同方向单轴压缩下, Ti3B4的变形行为显著不同, 说明Ti3B4的力学行为和变形机制具有很强的各向异性.当沿着a轴加载时, 层内Ti−Ti相互作用减弱使Ti3B4的承载能力降低, 导致后续压缩应力虽依旧单调递增但增加速率明显降低.接着, 层间Ti−Ti键和沿着b轴方向的B−B键断裂使 Ti3B4完全破坏.当沿着 b轴加载时, 首先Ti3B4中 Ti−B 化学键的变化, 包括层内 Ti−B 化学键减弱和层间Ti−B化学键增强, 导致Ti3B4结构发生了一定程度的扭曲.接着, 当压缩应变增加到临界应变时, Ti3B4结构完全破坏, 尤其是沿b轴方向B−B键断裂导致其无法继续承载, 造成压缩应力突降.当沿着c轴加载时, 层内Ti−B键的断裂和层间Ti−B键的形成导致Ti3B4结构处于不稳定状态, 承载能力降低.

通过DOS分布可知, Ti3B4初始结构呈现金属性.在低能区域, Ti3B4的DOS主要由B−2s和B−2p轨道组成; 在费米能级附近, 其DOS主要由Ti−3d 和 B−2p 轨道杂化形成.而 Ti3B4中的赝能隙主要由Ti−3d轨道独自形成.在单轴压缩下, 变形后的Ti3B4仍然呈现金属性.但是在a轴和b轴压缩下, 变形后的Ti3B4没有明显的赝能隙.在c轴压缩下, 变形后的Ti3B4中虽然依旧存在赝能隙, 但是向低能方向移动.同时赝能隙宽度变窄,表明变形后Ti3B4的共价性能降低.

本文为Ti3B4结构在非静水压力载荷下的力学行为、电子特性和变形机制提供了新的见解, 对提高其宏观性能以及设计合成性能优良的钛硼复合材料具有一定的理论意义.