简化圆锥曲线运算方法的探究
廖应春
(重庆市求精中学校 重庆 400015)
在圆锥曲线教学中常常发现,学生知道这道题怎么做,但结果却是错误的。表面的原因,是运算量太大。但深层次原因,却是学生的数学运算能力不强!数学运算是挡在学生解决圆锥曲线问题面前的一道难以跨越的坎!那么,如何跨越这道坎?笔者对此进行了一定的探究,得出一系列简化运算、减少运算量的具体方法,在此抛砖引玉,仅作参考。
一、巧设直线方程
直线方程的形式选择恰当,可以从源头上起到减化计算的效果。本文主要指以下三种形式的直线方程:
①纵截距式:y=kx+n
若直线l过y轴上的点(0,n),则设直线l:y=kx+n;若直线l与抛物线x2=2py联解,设直线l:y=kx+n。
②横截距式:x=my+n
若直线l过x轴上的点(n,0),则设直线l:x=my+n;若直线l与抛物线y2=2px联解,设直线l:x=my+n
③已知两点A(x1,y1),B(x2,y2),求直线AB的方程
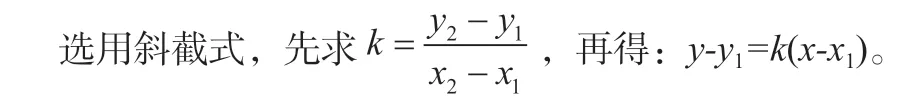
二、在分式运算中,要去分母,并注意分离常数
①去分母。分式运算,先去分母后运算。
②分离常数。在分式求和中,先分离常数,再求和。
三、多项式运算中,注意提取公因式、公倍数
多项式计算中,尽量先提取公因式、公倍数,如:
8(k+1)(k+2)+32(k2-1)=8(k+1)[(k+2)+4(k-1)]=8(k+1)(5k-2)
四、涉及多个变量或多个字母的运算
①把握主元(变量),区分常数与变量:当算式中含有多个(两个及以上)变量或字母时,认定哪个是主要变量,标记为主元,整个化简计算过程中都围绕着这个主元进行,而其它项可暂不作过多化简。

五、弦长公式和面积公式
求弦长、求三角形面积是圆锥曲线的常见题型,也是高考的重点题型。
(一)弦长公式
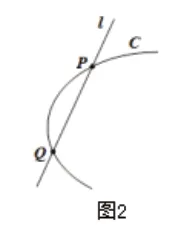
若直线l与曲线C相交于P(x1,y1),Q(x2,y2)两点(如图2),求弦长 .

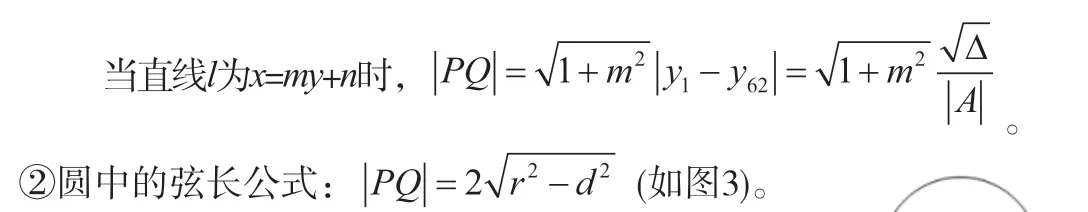
(二)面积公式
若直线l与曲线C相交于P(x1,y1),Q(x2,y2)两点(如图4),O为坐标原点,求ΔOPQ的面积。

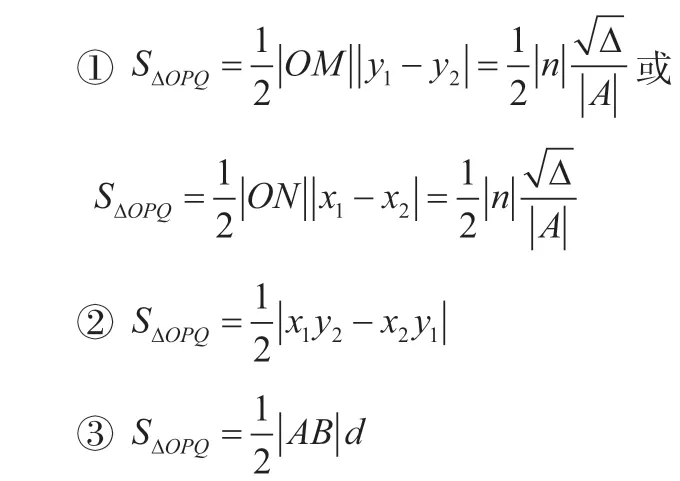
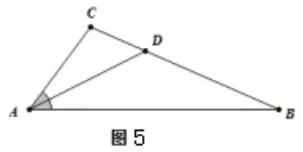
六、应用平几知识,有效转化条件

④三角形面积的转化:面积之比⇔边长之比⇔坐标之比
⑤利用相似三角形的相似比、平行线分线段成比例等转化。
教学实践表明,学生在解析几何题中往往还缺乏运用以上方法的意识,盲目运算的现象普遍存在。要改变这一现象,需要教师抓住每一次训练机会,通过例题讲解,不断有意识地加以引导,使学生逐步领悟这些方法的优点,提高运算能力,有助于培养学生的数学核心素养。