量子力学教学中Mathematica的简单应用
蒲 瑾
(西华师范大学物理与空间科学学院 四川南充 637002)
一、引言
量子力学是在20世纪初建立起来的以微观粒子运动规律为研究对象的一门重要理论。随着量子理论的深入研究,其对现代物质文明的发展发挥了举足轻重的作用。我们不仅已经见证了量子理论与麦克斯韦方程组伟大的结合,结果使得电磁场本质的研究大放异彩,而且量子理论在量子信息科学、量子化学、量子生物学、材料科学、天体物理等领域中也被广泛地应用。因此,如何让高等院校物理专业学生学好量子力学,是高校量子力学教师非常值得研究的一个重要课题[3-5]。
本文以一维谐振子和氢原子作为实例,阐述Mathematica软件在量子力学教学中的应用,复杂、抽象的公式被简单地图形化、可视化。这样,学生对量子力学物理本质的认识更加深刻,有助于增强学生的学习信心、激发学习动力。
二、在量子力学教学中Mathematica的应用实例
由于简谐运动在自然界中广泛地存在,它往往是被看做复杂运动的简单近似,因此,在理论和应用上研究谐振子运动都具有非常重要的意义[1-2]。设一维线性谐振子的势能为V(x)=mω2x2/2,则体系的薛定谔方程为:
很显然,由于束缚态的边界条件引起谐振子能量的量子化,并且其能级的分布是均匀的,即相邻能级间距为ħω。归一化的能量本征函数为:
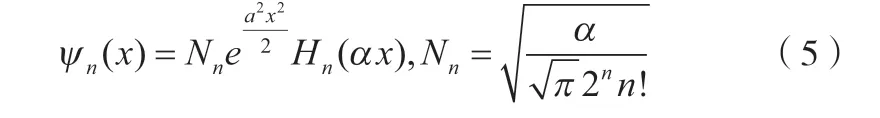
式中Hn(αx)是Hermite多项式。利用Mathematica编写程序绘制出本征函数ψn(x)和概率密度ωn(x)的分布图像,如图1所示。图中取α=1,实和虚曲线分别表示本征函数和概率密度。图中可以直观地反映出量子力学中线性谐振子的运动规律,有助于学生深刻理解这部分知识。同时,程序编写非常简单,直接调用程序中HermiteH[n,x]就可以轻松画出Hermite多项式。以n=3为例,Mathematica输入程序如下:
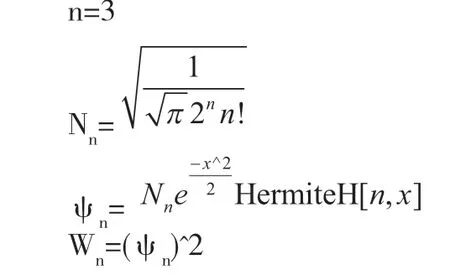

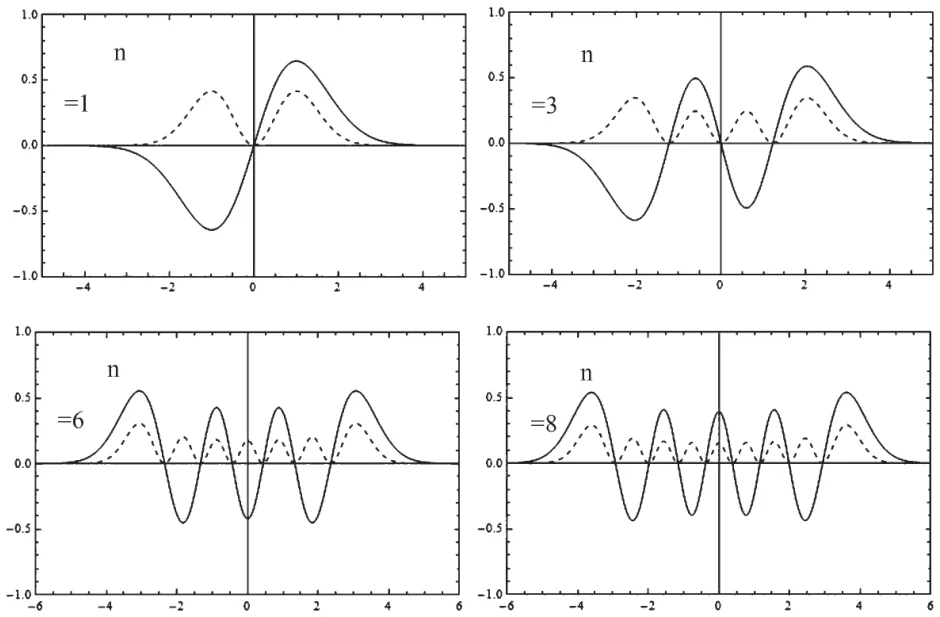
图1 能量本征函数和概率密度图
氢原子不仅可以通过薛定谔方程严格求解,而且是量子力学发展史上最突出的成就之一[1-2]。同时,氢原子是最简单的原子,是研究复杂原子和分子结构的基础[1-2]。让学生掌握通过薛定谔方程求解氢原子的能级和波函数的方法是非常重要的,但这个求解的过程比较复杂,讲解起来学生觉得非常枯燥,且结果也非常抽象。因此,让学生利用Mathematica来将结果图形化,激发学生自主探究,达到提高学习效果的目的,就显得非常重要。对于氢原子来说,原子核与电子之间的Coulomb势为V(r)=-e2/r,则在自然单位下,具有一定角动量的氢原子径向方程可表示为:
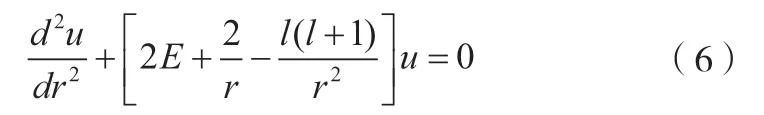
利用束缚态边界条件,方程(6)化为一个合流超几何方程。为了得到物理上的解,将无穷级数解F(-n+l+1,2l+2,2r/(na))中断为一个多项式,从而得到氢原子能级为En=-e2/(2an2),其中a为玻尔半径,主量子数n=1,2,3,…,角量子数l=0,1,2,…,n-1。径向函数为:
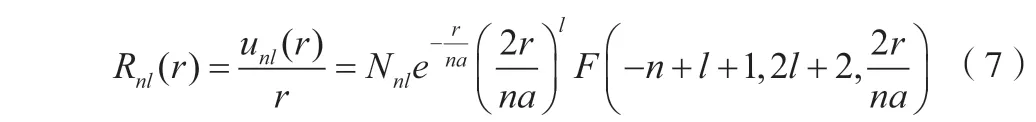
其中Nnl是归一化因子。于是,利用Mathematica可以画出氢原子中电子的径向概率分布,如图2所示。以n=3,l=1为例,采用原子单位,Mathematica输入程序如下:

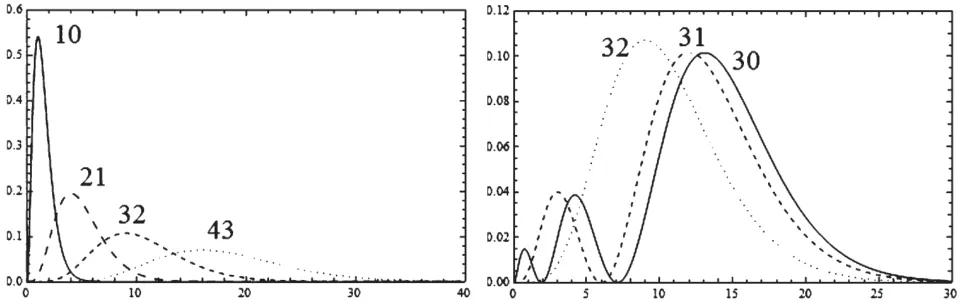
图2 氢原子中电子的径向概率分布图
通过让学生自己画图和观察图形,让学生理解量子力学中电子的位置呈概率分布,即电子并无严格轨道的概念。同时,通过观察径向概率分布曲线随量子数n和l的变化关系,进一步理解氢原子结构的特征。比如,径向波函数的节点数目在不包括无穷远点与原点时,满足nr=(n-l-1)关系[1-2]。在给定n时,l=n-1,nr=0的轨道对应的径向概率分布的最概然半径满足r=n2a[1]。
三、结束语
量子力学中存在许多的复杂计算和抽象结果,都可以利用Mathematica进行快速计算和图形化展示。本文只列举了较突出的一维谐振子和氢原子的问题,事实上,还可以利用Mathematica在量子力学教学过程中进行更多的科学计算和精准绘图。这样,量子力学的教学过程将更加有趣和生动,让教师有更充足的时间去加强量子理论本质的讲解。同时,可以通过课后练习,让学生动手去利用Mathematica进行实际操作,从而提高教学质量。

