面向空间近距离操作的机械臂与服务卫星协同控制

王兴龙，周志成，王典军，陈士明

(中国空间技术研究院通信卫星事业部，北京 100094)

0 引 言

航天器在轨服务是我国正在建设发展的重要航天系统工程之一[1-2]。目标卫星在轨捕获等空间近距离操作需要机械臂与服务卫星协同配合完成[3]。服务卫星通过导引、绕飞、逼近等轨道机动，最终悬停保持在目标卫星近距离处，为其搭载的机械臂提供稳定基座；机械臂通过轨迹规划与跟踪控制，实现目标捕获等空间操作。在此过程中，存在两个较为突出的问题：一方面，机械臂是一个典型的变结构强耦合的非线性系统，存在建模误差和外部扰动等很多不确定因素；另一方面，服务卫星与目标卫星的相对位置和姿态存在耦合，机械臂运动产生的反作用力/力矩又会对服务卫星控制产生干扰。

针对机械臂控制问题，谢箭等[4]提出了基于神经网络的自适应控制方法，对系统不确定因素具有较好的适应能力，但在线学习所需时间较长。Herman[5]和Hu等[6]采用滑模变结构方法设计机械臂控制器，具有响应快速、实时性强、鲁棒性高等特点，但控制误差容易产生抖颤现象且无法保证有限收敛时间。服务卫星相对位姿耦合控制方面，李鹏等[7]和Lu等[8]基于C-W方程和姿态四元数建立了相对位置和姿态耦合动力学模型。梁斌等[9]和郭碧波等[10]设计了基于视线的相对导航控制方法，Singla等[11]考虑参数不确定性设计了相对姿轨输出反馈控制律，但上述方法都未考虑机械臂运动对服务卫星控制的干扰。吴剑威等[12]利用遗传算法对机械臂运动轨迹进行优化，减小对卫星姿态的影响，但未涉及卫星控制器设计。史也[13]和斯祝华等[14]分别对机械臂和太阳帆板的干扰力矩进行估计补偿，并设计卫星控制律，但只考虑了其对卫星姿态控制的影响。徐文福等[15]基于微分运动学方程设计了机械臂捕获目标的协调控制方法，但同样未考虑基座卫星的位姿耦合问题。

本文提出一种面向空间近距离操作的机械臂与服务卫星协同控制方法。采用全局终端滑模控制设计机械臂轨迹跟踪控制律，采用PD控制设计服务卫星相对位姿耦合控制律，并通过前馈补偿方式实现两者的协同控制。最后通过仿真，验证控制方法的有效性。

1 系统动力学建模

1.1 机械臂和服务卫星组合体动力学模型

空间近距离操作示意如图1所示。研究服务卫星和目标卫星短时间近距离相对运动时，可将目标卫星轨道系∑to视为惯性系。除特别说明外，文中所有矢量均用其在∑to中的坐标分量表示。

基于多刚体系统建模理论，建立机械臂和服务卫星组合体动力学模型。系统基本假设定义如下：

假设1.机械臂臂杆和服务卫星均视为刚体，不考虑柔性振动和液体晃动等影响。

假设2.机械臂关节视为理想铰链，不考虑关节柔性和摩擦等非线性因素。

假设3.机械臂和服务卫星组合体处于失重环境中，不考虑重力梯度和其它环境影响。

根据上述假设，采用拉格朗日方程[16]推导得到机械臂和服务卫星组合体动力学方程为

(1)

(2)

特别地，当服务卫星在目标卫星近距离处悬停保持时，忽略控制误差，vs,ωs均可视为零，则式(2)可简化为基座固定机械臂动力学方程：

(3)

1.2 服务卫星和目标卫星相对位姿耦合模型

基于空间相对运动建模理论，建立服务卫星和目标卫星相对位姿耦合动力学模型。系统基本假设定义如下：

假设4.服务卫星和目标卫星运行在标准圆轨道，倾角和偏心率均可视为零，受到的轨道摄动均可忽略，两者相对距离远小于其轨道半径。

假设5.目标卫星视为刚体，不考虑其柔性振动和液体晃动等影响。

根据假设4，服务卫星和目标卫星之间的相对轨道运动可用C-W方程描述，推导得到两星相对位置动力学方程为

(4)

式中：rr,vr分别为服务卫星相对于目标卫星的位置和速度矢量在∑to中的分量，参数矩阵M1,C1,N1的表达式分别为

(5)

式中：ms为服务卫星的质量，Ω为目标卫星的轨道角速度标量，E为单位矩阵。

根据假设1和假设5，服务卫星和目标卫星均视为刚体，采用相对四元数建模方法推导得到两星相对姿态动力学方程为

(6)

式中：λrv为服务卫星相对于目标卫星的姿态四元数的矢量部分，sbωr为服务卫星相对于目标卫星的角速度矢量在服务卫星本体系∑sb中的分量，sbTs为服务卫星的控制力矩矢量在∑sb中的分量，参数矩阵B2,M2,C2,N2的表达式分别为

(7)

式中：λr0为服务卫星相对于目标卫星的姿态四元数的标量部分，sbIs,sbIt分别为服务卫星和目标卫星的转动惯量在∑sb中的表示，tbIt为目标卫星的转动惯量在自身本体系∑tb中的表示，sbωs为服务卫星的角速度矢量在∑sb中的分量。

定义相对位姿耦合状态变量：

(8)

联立式(4)和式(6)，整理得到服务卫星和目标卫星相对位姿耦合动力学方程为

(9)

式中：

(10)

式中：sbFs为服务卫星的控制力矢量在∑sb中的分量，Asb为∑sb到∑to的转换矩阵，体现了服务卫星与目标卫星的相对位姿耦合。

2 机械臂全局终端滑模控制

2.1 全局终端滑模控制器设计

为实现目标捕获等空间近距离操作，并考虑实际星载计算能力限制，设计采用机械臂与服务卫星协同控制策略。针对机械臂和服务卫星分别独立设计控制器。机械臂按基座固定方式控制，服务卫星控制误差产生的位姿变化作为机械臂控制器的扰动项。服务卫星进行相对位姿耦合控制，机械臂运动产生的反作用力和力矩作为前馈补偿叠加到服务卫星控制器中，实现两者的协同控制。

基于全局终端滑模控制方法设计机械臂控制器，实现机械臂在基座扰动等不确定因素影响下的精确轨迹跟踪，同时保证跟踪误差在全局范围的有限收敛时间。

在基座固定机械臂动力学模型的基础上，考虑各种不确定因素，机械臂动力学方程为

(11)

式中：ΔD为包括基座扰动等在内的不确定项。

ΔD=[Δd1,Δd2,…,Δdn]T

(12)

式(11)所示的机械臂动力学系统具有以下性质：

性质1.M(Θm)非奇异，且对称正定有界。

(13)

定义机械臂关节轨迹跟踪误差Em为

Em=Θmd-Θm=[em1,em2,…,emn]T

(14)

式中：Θmd,Θm分别为关节期望角度和实际角度。

构造全局终端滑模超平面S为

(15)

式中：

(16)

且有αi,βi>0，p,q为正奇数(p>q)。

假定ΔD有界，根据全局终端滑模控制方法，构造机械臂关节轨迹跟踪控制律为

(17)

式中：

(18)

(19)

且有φi,ηi>0，因而有γi>0，i=1,2,…,n。

2.2 控制系统稳定性分析

定理1.对于式(11)所示的机械臂动力学系统，在满足性质2条件下，全局终端滑模控制律(17)能够保证系统渐近稳定。

证.滑模面S对时间t求一阶导数，并将全局终端滑模控制律式(17)代入，整理得

(20)

由式(19)可得

(21)

将式(21)代入式(20)，并令H=diag(η1,η2,…,ηn)，整理得

(22)

选取Lyapunov函数为

(23)

将式(23)对时间t求导，并根据性质2，整理得

-STΦS-STHSq/p

(24)

将式(24)中的矩阵展开，写成元素求和形式，有

(25)

2.3 跟踪误差收敛时间分析

定理2.对于式(11)所示的机械臂动力学系统，在满足性质1条件下，全局终端滑模控制律(17)能够保证跟踪误差Em在有限时间内收敛到零。

证.根据性质1，M(Θm)非奇异，将不等式(22)两边乘以M-1(Θm)，又因为M(Θm)对称正定有界，因此存在矩阵Φ*,H*，满足

(26)

式中：

(27)

研究机械臂关节i的轨迹跟踪误差emi。定义tri为emi从初始状态si(0)≠0到滑模面si(tri)=0的收敛时间，根据式(26)可得其微分方程为

(28)

从而解得

(29)

在滑模面si=0上，定义tsi为emi从初始状态emi(tri)≠0到零点emi(tri+tsi)=0的收敛时间，根据式(15)可得其微分方程为

(30)

从而解得

(31)

定义ttotal为机械臂所有关节的轨迹跟踪误差在全局范围内从初始状态到零点的总收敛时间：

(32)

3 服务卫星相对位姿耦合控制

3.1 相对位姿耦合误差模型

为实现在目标卫星近距离处的悬停保持，服务卫星采用相对位姿耦合控制。定义相对位置、速度、姿态和角速度控制误差er,ev,eΛ,sbeω分别为

(33)

式中：rrd,vrd分别为服务卫星相对于目标卫星的期望位置和期望速度矢量在∑to中的分量，Λr,Λrd分别为服务卫星相对于目标卫星的实际和期望姿态四元数，eΛ0,eΛv分别为eΛ的标量部分和矢量部分，sbωrd为服务卫星相对于目标卫星的期望角速度矢量在∑sb中的分量。

定义相对位姿耦合控制误差：

(34)

将式(33)和式(34)代入式(9)，并考虑机械臂反作用力和力矩，整理得到相对位姿耦合误差动力学方程为

(35)

式中：urm为机械臂反作用力和力矩矢量在∑sb中的分量。

3.2 相对位姿耦合控制器设计

为实现协同控制，服务卫星采用“前馈补偿+PD控制”的方法，根据动力学模型估算机械臂反作用力和力矩，并将其作为前馈补偿叠加到相对位姿耦合PD控制器中。服务卫星相对位姿耦合控制结构如图2所示。

图2 服务卫星相对位姿耦合控制结构Fig.2 Coupled control structure for relative position andattitude of servicing satellite

(36)

(37)

采用前馈补偿+PD控制方法，构造服务卫星相对位姿耦合控制律为

(38)

式中：KP,KD分别为比例和微分系数。通过KP,KD的合理取值，可以保证式(35)所示的相对位姿耦合误差动力学系统渐进稳定。

4 仿真校验

4.1 工程算例

通过工程算例在MATLAB和ADAMS联合仿真平台上进行仿真，验证本文控制方法的有效性。机械臂设定为7自由度空间机械臂，整体构型与国际空间站遥控机械臂系统(SSRMS)相似，D-H坐标系如图3所示，D-H参数如表1所示，动力学参数如表2所示。服务卫星和目标卫星设定采用某成熟型号卫星平台，动力学参数如表3所示。

图3 空间7自由度机械臂D-H坐标系Fig.3 D-H frames of 7-dof space manipulator

表1 机械臂D-H参数
Table 1 D-H parameters of manipulator

臂杆iθmi/ (°)αi/(°)ai/mdi/m1θm19000.452θm2-9000.33θm302.70.34θm402.70.35θm59000.36θm6-9000.37θm7000.6

表2 机械臂动力学参数Table 2 Dynamic parameters of manipulator

表3 服务卫星和目标卫星动力学参数Table 3 Dynamic parameters of servicing and target satellites

机械臂全局终端滑模控制和服务卫星相对位姿耦合控制的参数分别为

(39)

4.2 仿真结果

图4 机械臂关节角度跟踪误差Fig.4 Tracking errors of manipulator joint angles

图5 机械臂关节角速度跟踪误差Fig.5 Tracking errors of manipulator joint angular velocities

图6 机械臂关节控制力矩Fig.6 Control torques of manipulator joints

服务卫星相对位姿耦合控制仿真得到的相对位置、速度、姿态和角速度误差er,ev,eΛv,sbeω分别如图7～10所示，服务卫星控制力和力矩sbFs,sbTs分别如图11～12所示。从图7～12可以看出，在捕获过程的全部时间内，er,ev,eΛv,sbeω能够被控制在期望精度，满足控制要求。sbFs,sbTs三轴分量的最大绝对值分别小于20 N和60 N·m，不超过设计限定值，工程实现可行。

图7 服务卫星相对位置误差Fig.7 Relative position errors of servicing satellite

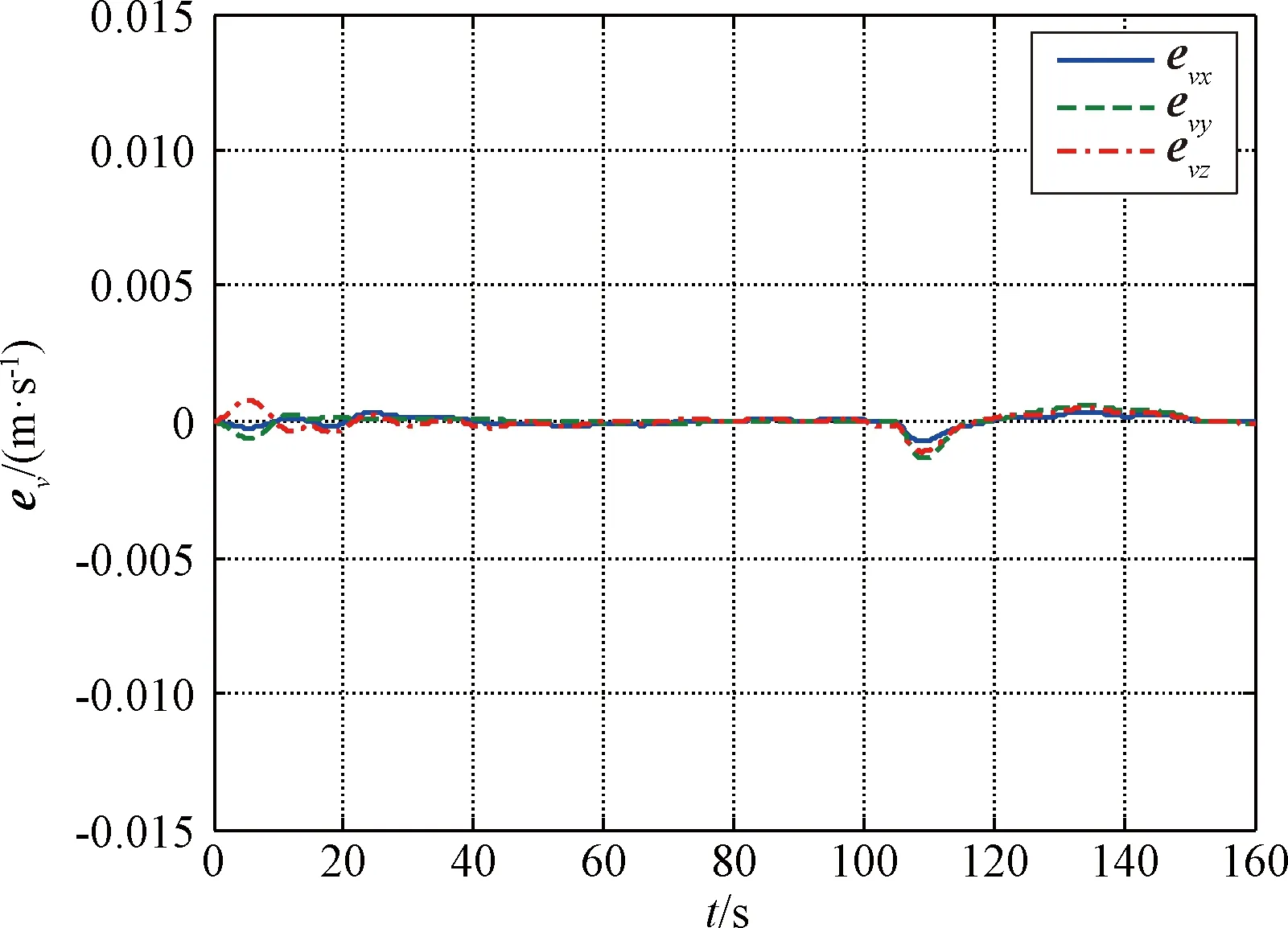
图8 服务卫星相对速度误差Fig.8 Relative velocity errors of servicing satellite

图9 服务卫星相对姿态误差Fig.9 Relative attitude errors of servicing satellite

图10 服务卫星相对角速度误差Fig.10 Relative angular velocity errors of servicing satellite

图11 服务卫星控制力Fig.11 Control forces of servicing satellite

图12 服务卫星控制力矩Fig.12 Control torques of servicing satellite

5 结 论

本文针对空间近距离操作涉及的动力学与控制问题，提出了一种机械臂与服务卫星协同控制方法，并通过数值仿真验证了方法的有效性和适用性。方法具有以下特点：1)能够有效实现机械臂的精确轨迹跟踪控制，并保证一定的控制精度、稳定性和误差收敛时间；2)能够实现服务卫星在机械臂反作用力和力矩影响下的相对位姿耦合控制，协同完成空间近距离操作任务。

应当指出，该控制方法还存在一定问题，如计算复杂，每个控制周期都需要实时解算系统动力学模型，对控制系统硬件性能要求较高。考虑工程实用性，可以预先算出服务卫星和机械臂几种典型构型的动力学参数，工程实施时根据需要直接调用相应参数生成控制力和力矩，由此带来的建模误差通过控制律鲁棒项予以补偿。