定时定点月面着陆全程轨道控制设计
李革非,刘 勇,郝大功,马传令
(1. 北京航天飞行控制中心,北京 100094;2. 航天飞行动力学技术重点实验室,北京 100094)
0 引 言
2018年12月8日“嫦娥四号”月球探测器由长征三号乙运载火箭发射,开始了人类首次月球背面软着陆之旅。根据“嫦娥四号”月球背面软着陆任务设计方案,探测器经历地月转移、近月制动、环月飞行,择机实施动力下降,在月球背面冯·卡门撞击坑实现人类首次月球背面软着陆[1]。
月面定点软着陆对进行月面勘测或载人登月都有着重要的意义[2]。“阿波罗”工程后期的飞行实践表明,探测器完全可以在月球表面预定位置准确降落,实现定点着陆[3]。众多文献对在地外天体探测中实现定点着陆的轨道设计问题进行了研究,常用的变轨策略有圈次调整、调相轨道和轨道面调整等[4-9]。文献[4]在讨论不同地月转移轨道方案的基础上,考虑了调整地月转移时间、环月轨道倾角、月面下降圈次和调相轨道等月面定点着陆方案。文献[5-6]的研究表明,除了变轨策略设计,定点着陆动力下降过程中制导、导航与控制系统(GNC)精确调整纵向和横向航程的能力,也是成功实现地外天体定点着陆的关键因素。文献[7-8]重点对采用调相轨道和调整轨道平面的定点着陆策略进行了初步比较分析。文献[9]提出了在近月制动期间通过轨道面修正调整着月点经度。文献[10]设计了环月非对称降轨控制策略。文献[11]通过对不同定点着陆变轨策略进行比较分析,推荐月面定点着陆的变轨策略为降轨变轨2对2的瞄准策略和轨道平面调整机动策略。另外,文献[12-19]对月球软着陆动力下降轨道优化控制进行了研究。文献[20]针对小天体环境存在参数不确定性及初始状态偏差的特点,提出了一种考虑跟踪制导的着陆轨迹闭环优化方法,提高着陆位置和速度精度。上述文献主要解决的是月面定点着陆的轨道控制问题。
探测器月面着陆及后续月面巡视工作受着陆区位置和范围、测控支持、光照及能源等多项约束条件的限制,提出了探测器定时着陆于预定着陆区的严格要求。如文献[21]指出,相对于月球正面大面积平坦的月海区域,月球背面地形整体崎岖复杂,地形地貌的变化会对探测器的软着陆探测产生一定的影响。对照“嫦娥三号”和“嫦娥四号”的月面着陆区域,“嫦娥三号”着陆区经度范围约16.4°、纬度范围约3°,而“嫦娥四号”着陆区范围减小到经度范围约4°、纬度范围约2°。因此,相比“嫦娥三号”实现月面软着陆的要求,“嫦娥四号”提出了定时定点月面软着陆的更加严格的要求。
因此,本文提出了一种定时定点月面着陆全程轨道控制设计方法。针对定时定点月面着陆的目标要求,进行了包括地月转移、近月制动、环月降轨和动力下降的全程轨道控制的分段设计和联合规划,在入轨轨道偏差条件下,通过重新设计分段轨道控制目标,实现了接近标称飞行条件下的定时定点月面着陆。
1 月面着陆飞行过程
以“嫦娥四号”月球探测器为例。月面软着陆探测飞行过程分为发射段、地月转移段、环月段、动力下降段和月面工作段[2],如图1所示。
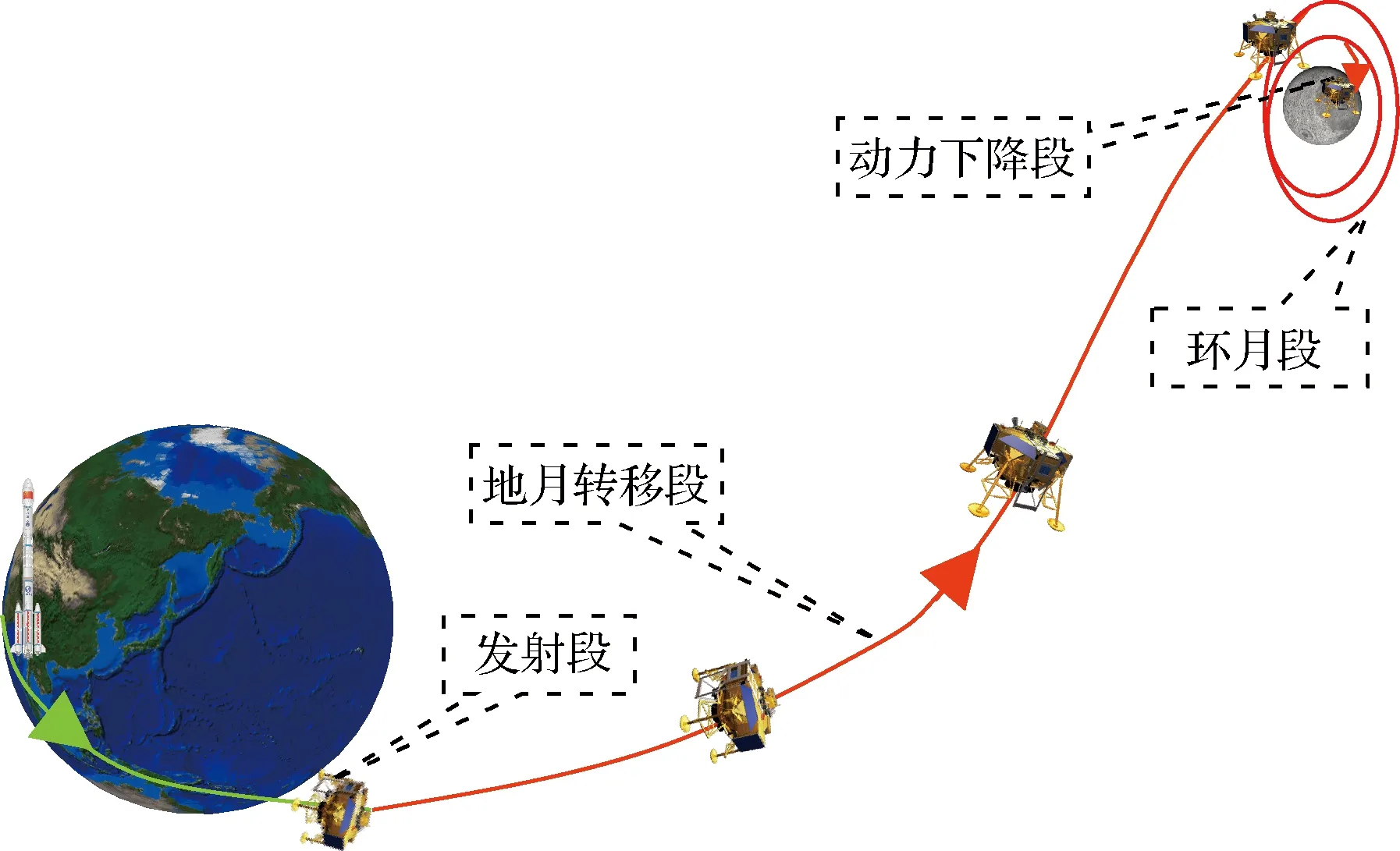
图1 探测器月面软着陆飞行过程示意图Fig.1 Sketch of lunar probe’s soft landing flight process
1)发射段:从运载火箭发射至器箭分离。探测器由运载火箭提供进入地月转移轨道的速度,探测器直接进入倾角28.5°、近地点约200 km,远地点约380000 km的大椭圆地月转移轨道。
2)地月转移轨道段:探测器与运载火箭分离到探测器执行近月制动前的飞行过程,地月转移时间约4~5天,期间进行2~3次中途修正,最终到达高度约100 km的近月点。
3)环月段:从近月制动开始到动力下降开始前的飞行过程。近月制动后,探测器首先进入约100 km高的环月近极轨圆轨道;在100 km环月近圆轨道上运行若干天,根据实际轨道与目标着陆区的匹配性,择机进行环月轨道修正,微调轨道周期和轨道倾角,以实现着陆于目标着陆区内;在100 km环月近圆轨道运行若干天后,变轨进入100 km×15 km环月椭圆轨道。在100 km×15 km环月椭圆轨道运行若干天,以满足精确测定轨和探测器下降着陆前的要求,随后从高度约15 km的近月点开始动力下降过程。
4)动力下降段:从高度15 km开始至抵达月面的着陆过程。探测器动力下降过程分为7个阶段,包括着陆准备段,主减速段,快速调整段,接近段,悬停段,避障段,缓速下降段,最后软着陆于目标着陆区。
2 定时定点月面着陆轨道控制设计
2.1 探测器动力学方程
月球探测器的动力学方程可以建立在地心天球坐标系中,也可建立在月球天球坐标系中。
地心天球坐标系的动力学方程如下:
(1)

2.2 飞行目标和设计约束
月球探测器定时定点着陆月面的飞行轨道控制要求为:对应确定的发射入轨时刻,探测器在预定的着陆时刻着陆于预定的月面着陆点。按照探测器着陆月面的飞行过程,通过中途修正、近月制动、环月修正、环月降轨和动力下降的五段轨道控制实现探测器在月面定时定点着陆。
环月修正是在环月轨道出现偏差情况下,对月面着陆进行精确修正的补充控制。因此,探测器定时定点月面着陆的全程轨道控制针对中途修正、近月制动、环月降轨和动力下降进行分段设计和联合规划。
全程轨道控制设计的思路是:当入轨轨道存在偏差时,在全程飞行时间和分段飞行时间不变的条件下,重新设计中途修正、近月制动、环月降轨的飞行轨道和控制参数,使得探测器仍按照标称着陆时间着陆于标称着陆点。
按照飞行阶段相对独立,每一阶段飞行轨道与标称轨道基本相符合的思路,针对确定的发射窗口,定时定点月面着陆全程轨道控制的设计约束包括:1)地月转移轨道到达近月点的时刻不变;2)近月制动到环月降轨的飞行时间基本不变;3)环月降轨到动力下降的飞行时间基本不变。定时定点月面着陆全程轨道控制设计参数包括:1)中途修正控制参数和瞄准目标参数;2)近月制动控制参数和瞄准目标参数;3)环月降轨控制参数和瞄准目标参数。
2.3 中途修正控制
2.3.1中途修正控制变量和目标参数设计
中途修正的目标是使探测器到达近月点的近月点高度和轨道倾角满足预定目标。
中途修正控制时刻是结合探测器测控约束人为确定的。地月转移轨道飞行时间遵循标称轨道设计的飞行时间。
中途修正的控制模型如下:
初始状态:入轨轨道。
约束参数:中途修正控制时刻人为确定。
控制变量:中途修正控制速度增量ΔvM=[ΔvMx,ΔvMy,ΔvMz],即控制变量为XM=ΔvM,其中,ΔvMx,ΔvMy,ΔvMz为中途修正速度增量在惯性系的三方向分量。
2.3.2中途修正求解算法
中途修正求解采用摄动制导方法。探测器转移轨道的终端状态为初始状态的函数,初始状态P为当前时刻探测器轨道参数的位置和速度,终端状态Q根据目标轨道的不同要求而选择不同参数,则函数形式为Q=f(P)。
摄动制导方法的基本思想为,探测器实际轨道与标称轨道的偏差为小量,从而将实际轨道在标称轨道附近泰勒展开,保留线性项,得到如下线性控制方程:
(2)
式中:ΔQ为终端时刻探测器实际状态Q与标称状态QN的偏差,即ΔQ=Q-QN;ΔP为控制矩阵;K为状态变量对控制参数的敏感矩阵,也称雅可比矩阵。
若初始参数P0对应的初始终端参数Q0与要求的目标终端参数QT存在一定偏差,利用式(2),通过迭代计算修正终端参数偏差Q0-QT所需的初始参数修正量ΔP为:
ΔP=K-1·ΔQ
(3)
如果控制变量个数与目标参数个数不相等,则可利用最小范数广义逆计算控制变量ΔP为:
ΔP=KT(K·KT)-1·ΔQ
(4)
式中:ΔP=XM,ΔQ=YM。

中途修正速度增量按照先脉冲推力、后有限推力进行迭代精细求解。
2.4 近月制动控制
2.4.1近月制动控制变量和目标参数设计
在地月转移轨道终点,探测器相对于月球的轨道为双曲线轨道,为了使其变为环月轨道,必须做减速机动。近月制动必须在探测器到达近月点附近实施,通过一次近月制动实现环月轨道。
近月制动的控制模型如下:
初始状态:中途修正后轨道。
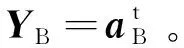
约束参数:控制时刻脉冲点位于近月点,控制采用横向脉冲。
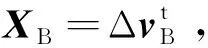
2.4.2近月制动求解算法
利用活力公式计算近月制动控前轨道和控后轨道的速度,其速度差值即为近月制动的脉冲推力速度增量:
(5)
式中:μ为月球引力常数,r为月心距,a为半长轴,v为探测器速度。
在进行有限推力计算时,推力方向为近月点的横向方向、迭代计算过程中保持惯性空间不变。速度增量仍采用式(5)修正,开机点按照发动机开机长度以近月点为中点平分。迭代计算过程如下:
(1)计算脉冲推力速度增量vBt,作为有限推力速度增量的初值。
(2)有限推力积分到速度增量等于vBt。
(3)计算关机点的速度voff和月心距roff。

(5)如果|vBt-voff|<ε则结束;否则修正有限推力速度增量v′Bt=vBt+(vBt-voff),返回(2)。
2.5 环月降轨控制
2.5.1环月降轨控制变量和目标参数设计
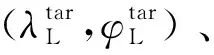
对于环月圆轨道,其水平方向与横向方向重合,水平脉冲控制点对面是近月点或远月点。但实际轨道不是理想的圆轨道,近月点对面的水平脉冲不能使控后轨道同时满足近月点高度和近月点真近点角的要求。因此,若使得环月降轨只用一次控制实现近月点的高度和真近点角满足要求,必须调整控制姿态或者控制点。本文采用调整控制点的方式。
环月降轨的控制模型如下:
初始状态:近月制动后轨道。
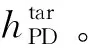
约束参数:动力下降点时刻与着陆点时刻按照动力下降段时间相匹配,TL=TPD+ΔTPD;动力下降点位置与着陆点位置按照动力下降段航程相匹配;环月降轨与动力下降之间的轨道飞行圈数固定。
控制变量:环月降轨控制时刻tHD,速度增量ΔvHD=[ΔvHDr,ΔvHDt,ΔvHDn]=[0,ΔvHDt,0],即控制变量为XHD=[tHD,ΔvHDt]。
2.5.2环月降轨求解算法
根据高斯摄动方程,只有横向速度增量Δvt,近月距rp的控制方程为:
Δvt=
(6)
近月点幅角控制方程为:
(7)
根据方程(6)~(7),以控制近月距和近月点幅角的脉冲控制参数作为初值,用广义牛顿迭代法精确计算有限推力的控制点和速度增量,使控后轨道满足动力下降点的近月点高度和近月点幅角的要求。
2.6 着陆点与动力下降点的匹配转换
探测器环月降轨后,经过动力下降控制,降落到月面着陆。动力下降段为探测器自主控制。对于标称轨道而言,动力下降段的飞行过程是固定的,飞行时间和下降航程保持不变,因此,着陆点位置和动力下降点位置是相互匹配的,同时,着陆点时间与动力下降点时间也满足固定的时序。
设动力下降段航程ΔLPD为惯性坐标系的航程,动力下降段飞行时间为ΔTPD,根据轨道倾角i,着陆点位置(λL,φL)和动力下降点位置(λPD,φPD)可进行相互转换。
2.6.1根据动力下降点位置计算着陆点位置
已知:轨道倾角i,动力下降点经纬度(λPD,φPD),动力下降航程ΔLPD,动力下降飞行时间ΔTPD。

图2 动力下降点与着陆点Fig.2 Power descent point and landing point
1)由倾角和动力下降点纬度计算着陆点纬度
如图2所示,设C为动力下降点,B为着陆点,根据倾角和动力下降点纬度,采用正弦定理可得:
升轨着陆:
降轨着陆:
则着陆点纬度为:
2)由倾角和动力下降点纬度计算着陆点经度
升轨着陆点经度:

ωmΔTPD
降轨着陆点经度:
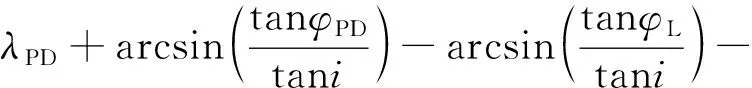
ωmΔTPD
式中:Rm,ωm分别为月球平均半径和月球自转角速度。
2.6.2根据着陆点位置计算动力下降点位置
动力下降点纬度为:
升轨着陆动力学下降点经度:
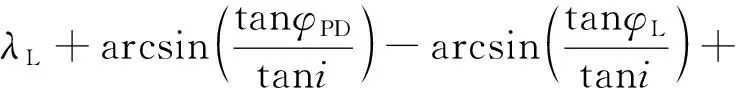
ωmΔTPD
降轨着陆动力下降点经度:
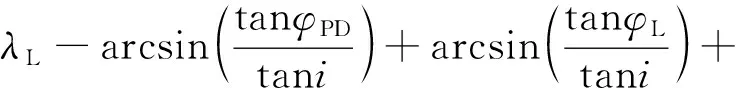
ωmΔTPD
2.7 定时定点着陆偏差修正
环月降轨后实际轨道与标称轨道的周期偏差和轨道平面偏差均会影响探测器无法在标称着陆时刻着陆在标称着陆点。为实现定时定点着陆,必须对轨道平面偏差和轨道周期偏差进行修正。
2.7.1着陆位置偏差与轨道倾角修正
在实际动力下降点时刻建立瞬时惯性系。在动力下降过程中,探测器星下点固联在月球上随月球运动,在该瞬时惯性系中,探测器标称着陆点在标称着陆时刻的赤经,需考虑标称着陆时刻与实际着陆时刻的时间偏差和动力下降过程中由于月球自转引起的着陆点经度变化。实际动力下降点时刻瞬时惯性系如图3所示。
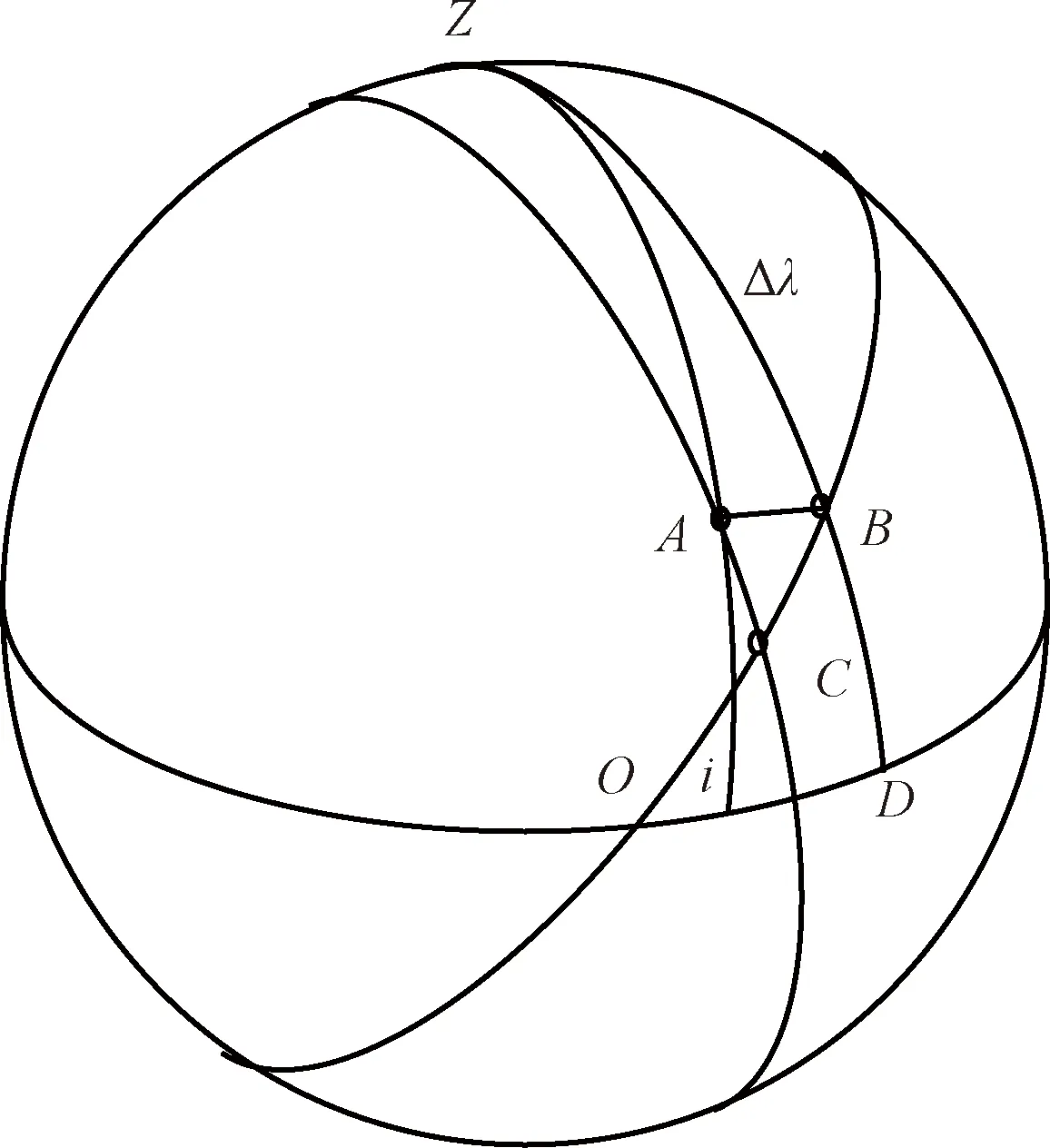
图3 着陆点偏差与轨道平面偏差Fig.3 Landing point deviation and orbit plane deviation
标称着陆时刻的着陆点A赤经为:
着陆点A纬度为:
着陆点A位置矢量为:
RLA=[RLAx,RLAy,RLAz]
式中:RLAx=cosφLAcosλLA,RLAy=cosφLAsinλLA,RLAz=sinφLA。
在实际动力下降点时刻瞬时惯性系中,根据实际轨道倾角i,实际动力下降点位置(λPD,φPD),动力下降段航程ΔLPD,计算实际着陆点B的位置(λLB,φLB)。由于动力下降段航程ΔLPD为惯性系航程,计算着陆点B赤经时不需要再考虑动力下降段飞行时间ΔTPD的影响。
实际着陆时刻的着陆点B位置矢量为:
RLB=[RLBx,RLBy,RLBz]
式中:RLBx=cosφLBcosλLB,RLBy=cosφLBsinλLB,RLBz=sinφLB。
由于实际着陆点与标称着陆点不在同一轨道面内,通过轨道平面控制,可将实际着陆点修正到标称着陆点,而轨道控制点即为这两个轨道平面的交点。根据轨道控制点的位置矢量,可计算控前轨道平面与控后轨道平面之间的夹角。
设轨道平面修正控制点C的纬度幅角为uC,实际动力下降点时刻的轨道升交点赤经为Ω。在实际动力下降点时刻的瞬时惯性系中,根据球面三角公式,轨控点的位置为:
λC=Ω+ΔλC, ΔλC=tanuC·cosi
φC=arcsin(sini·sinuC)
轨控点的位置矢量为:
RC=[RCx,RCy,RCz]
式中:RCx=cosφCcosλC,RCy=cosφCsinλC,RCz=sinφC。
分别计算标称着陆点和实际着陆点的轨道平面法向方向,NAC=RA×RC,NBC=RB×RC。
轨道平面偏差由轨道倾角偏差和升交点赤经偏差组成。考虑到轨道倾角偏差主要引起着陆位置偏差,而升交点赤经偏差主要引起着陆时间偏差,因此,轨道平面偏差α即为轨道倾角偏差。
2.7.2着陆时间偏差与环月轨道周期修正
将实际动力下降点时间与标称动力下降点时间的偏差归算为从近月制动到动力下降的飞行轨道的周期差:
其中,QB_HD为近月制动到环月降轨的飞行圈数,QHD_PD为环月降轨到动力下降的飞行圈数。
轨道周期修正为:
修正后的近月制动瞄准目标半长轴为:
3 仿真算例
以嫦娥四号为例,设探测器定时定点着陆月面任务要求如下:探测器发射入轨时间为2018- 12- 08T02:42:30,动力下降时间为2019- 01- 03T10:15:00。地月转移轨道飞行110 h;近月制动到环月降轨轨道飞行217圈;环月降轨到动力下降轨道飞行52圈;动力下降圈为环月轨道268圈,动力下降航程450 km,动力下降时间600 s,动力下降点高度15 km;着陆点月面经度177.5°,月面纬度-45.5°。
1)标称入轨轨道
轨道历元:T=2018- 12- 08T02:42:30;
轨道根数:a=213417 km,e=0.969,i=28.5°,Ω=354.36°,ω=145.44°,M=0.73°。
地球引力场模型采用JGM-3,月球引力场模型采用GL0420A;在地月转移段,采用地心J2000惯性系,摄动考虑地球引力场阶次32×32,太阳、月球质点引力和光压,月球引力场阶次8×8;在月球捕获段和环绕段,采用月心J2000惯性系,摄动考虑月球引力场阶次64×64,太阳、地球质点引力和光压,地球引力场阶次8×8。
在推力作用段,采用4阶RK (Runge-Kutta)单步法积分器,积分步长为1 s。在自由飞行段,采用10阶KSG(Krogh-Shampine-Gardon)多步法积分器,积分步长为30 s。
中途修正轨道控制在入轨后24 h,即2018- 12- 09T02:42:30,近月制动控制时刻为2018- 12- 12T16:39:30,环月降轨在2018- 12- 30,具体控制时刻迭代计算得到。
中途修正初始瞄准目标为:近月点高度100 km,月球轨道倾角90°;近月制动初始瞄准目标为:环月轨道半长轴1837.4 km,即100 km环月圆轨道;环月降轨控制点初始位置与动力下降点位置的相位相差180°。表1为迭代计算结果,TCM表示中途修正,LOI表示近月制动,DHP表示环月降轨,iaim表示中途修正瞄准目标倾角,aaim表示近月制动瞄准目标半长轴,Δv表示速度增量,ton表示控制时刻。
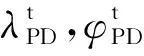
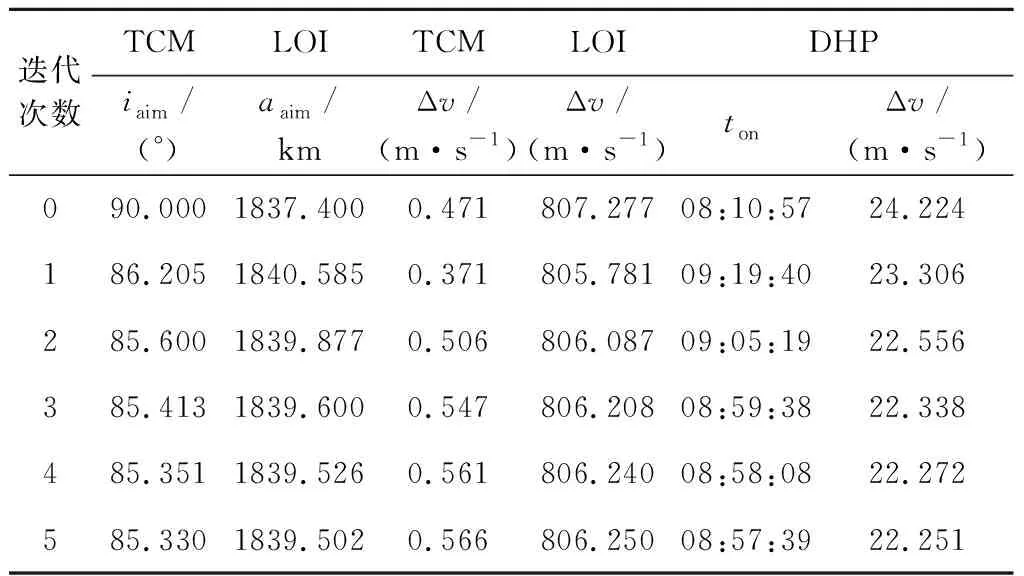
表1 标称入轨轨道的瞄准目标和速度增量Table 1 Aiming target and velocity increment for nominal injection orbit
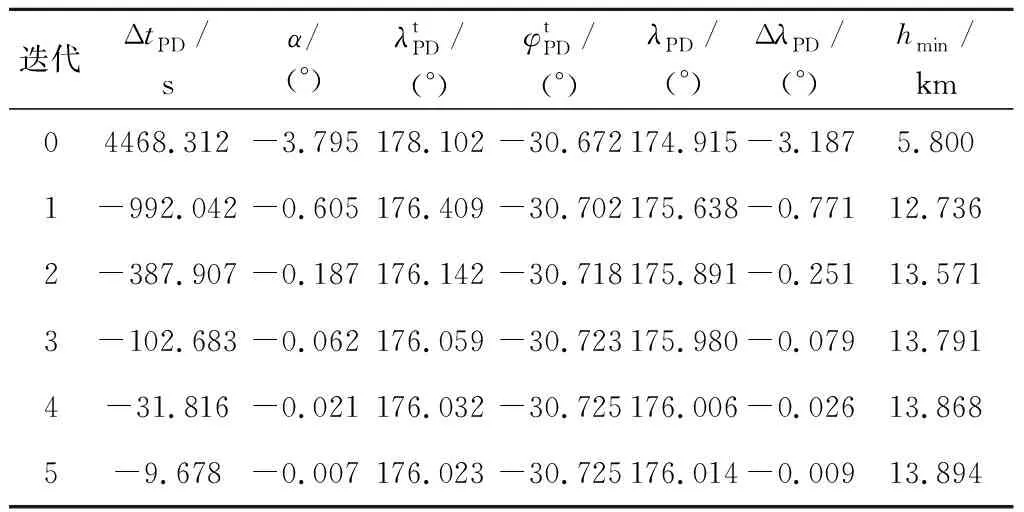
表2 标称入轨轨道的动力下降点参数Table 2 Power descent parameters for nominal injection orbit
在5次迭代计算中,瞄准目标倾角从初值90°逐渐迭代至85.330°,瞄准目标半长轴从初值1837.4 km逐渐迭代至1835.502 km。动力下降时间差从初始的4468 s收敛至10 s内,轨道平面差从初始的-3.795°收敛至-0.007°。迭代过程中,动力下降点目标位置经度和纬度是依据实际轨道倾角和标称着陆点位置匹配转换计算得到的,在迭代计算中是变化的。计算中以目标纬度为参照量计算动力下降时刻,因此,实际纬度与目标纬度一致。动力下降点经度差从初始的-3.187°收敛至-0.009°。环月降轨后,轨道最低月面高度从初始的5.8 km变为最终的13.894 km,很好地保证环月降轨后到动力下降前的飞行安全性,避免了撞月的风险。
2)偏差入轨轨道
正偏差入轨轨道:Δhp=-30 km,Δha=+7000 km,Δi=+0.1°,ΔΩ=-0.3°,Δω=+0.3°。
负偏差入轨轨道: Δhp=+30 km,Δha=-7000 km,Δi=-0.1°,ΔΩ=+0.3°,Δω=-0.3°。
表3列出了标称轨道与偏差轨道关键参数的比较。
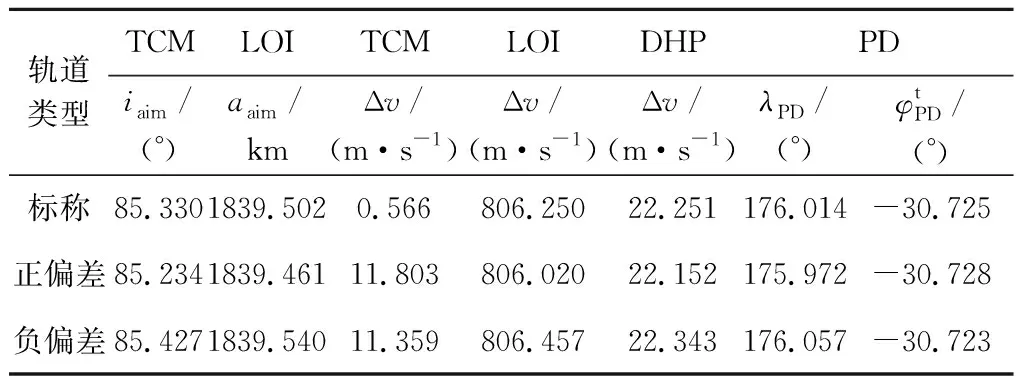
表3 标称轨道与偏差轨道的比较Table 3 Comparison of nominal orbit and deviation orbit
表3表明,正偏差轨道和负偏差轨道算例关于动力下降点时间差、轨道平面差的迭代计算收敛过程与标称入轨轨道基本一致,动力下降点目标位置和实际位置的迭代计算收敛过程也与标称入轨轨道基本一致。偏差轨道与标称轨道相比较,偏差轨道中途修正控制量约11.3~11.8 m/s,近月制动控制量相差约0.23 m/s,环月降轨控制量相差约0.1 m/s,制动和降轨控制量相差较小;瞄准目标倾角相差0.1°,瞄准目标半长轴相差约40 m,瞄准目标参数相差较小。表明,偏差轨道情况下,中途修正的控制量主要用于消除入轨轨道偏差,偏差轨道经过中途修正后,轨道与标称轨道飞行基本一致,很好地保证了近月制动、环月降轨和动力下降的飞行控制和飞行时序基本不变。
4 结 论
本文针对月球探测器入轨偏差轨道,通过对中途修正、近月制动、环月降轨和动力下降的全程四个飞行阶段轨道控制的联合规划,实现探测器按照预先设计时间着陆于预定着陆点,实现定时定点的月面着陆。提出了着陆位置偏差通过轨道倾角修正和着陆时间偏差通过环月轨道周期修正,在全程轨道控制设计时,分别对月球轨道目标倾角和环月轨道目标半长轴进行了修正设计。全程轨道控制的分段设计和联合规划,优化设计了分段控制的瞄准目标,重构了地月转移轨道和环月轨道,实现了与标称状态基本一致的定时定点月面着陆。
本文提出的定时定点全程轨道控制设计方法,既构建了全程轨道设计,又完成了各段轨道控制参数计算,可应用于月球着陆、月球采样返回以及载人登月等要求月面定时定点着陆任务的轨道设计和控制实施。

