自然形高空气球上升过程形状预测
杨泽川,罗汝斌,廖 俊,蒋 祎,袁俊杰,王 宁,李 珺
(1. 中南大学航空航天学院,长沙 410083;2. 北京宇航系统工程研究所,北京 100076)
0 引 言
高空气球是一种可在临近空间高度范围工作、搭载多种任务载荷系统的多用途浮空平台,具有驻空时间长、效费比高、安全性好等优点,在预警探测、侦察监视、导航通信等领域有广泛的应用前景[1-2]。
高空气球作为一种无动力浮空器,其动力学特性对于高空浮空器的快速部署至关重要。因此,很多学者针对高空气球上升段动力学特性进行了研究。文献[3]建立了气球上升过程的运动模型和热模型,计算了气球上升的轨迹,并与飞行数据相比较,有较好的吻合。文献[4]通过建立气球上升过程中温度微分方程和运动微分方程,运用两节点模型计算了标准大气模型下高空气球的上升轨迹、上下表面及球内温度变化等情况。文献[5]采用大涡模拟的方法研究了不同球体间距对“球形囊体型”浮空器气动特性的影响。文献[6-7]精确模拟了高空超压气球的运动特性和热力学特性,并分析了蒙皮膜的辐射特性和云对气球热力学的影响,研究不同大气模型对高空气球升空过程中的高度、氦气温度的变化曲线,分析了不同大气模型对气球热动力学性能的影响。上述研究表明,在上升过程中,高空气球的体积、速度等特性受到多因素的影响,进而影响浮空器的部署时间,因此,有必要针对浮空器上升过程中的体积以及速度等进行详细研究。
文献[8]对高空气球上升阶段与驻空过程中的动力学进行了仿真,上升速度曲线由于氦气“超冷”现象呈现双“V”形变化。文献[9]仿真了零压气球的飞行轨迹,通过真实飞行数据验证了仿真的正确,研究了影响气球在漂浮区域高度稳定性的有效参数,对充气量进行预测估计,使气球在不需要压舱物的情况下保持爬升的稳定性。文献[10]建立了一种新的描述气球热力学和动力学特性的动态模型,分析了初始放飞条件对气球飞行性能的影响,其中气球的充气量是影响上升速率最主要的因素。文献[11]通过采用零压气球受力平衡方程分析了平流层高空气球在升空过程中体积变化情况,并通过有限元方法验证了数值计算的准确性,研究结果表明体积和充氦量是高空气球的重要设计指标,其直接决定着高空气球的升空高度与载荷携带能力。
研究高空气球升空过程中的体积变化情况,对于高空气球的总体设计具有重要的实用价值。气球在上升过程中体积的增大会造成蒙皮应力的增大,不合理的气球体积以及充氦量设计可能会导致气球在上升阶段就由于蒙皮的应力过大而撕裂[12]。针对自然形高空气球,国内外诸多学者进行了气球的形状预测以及蒙皮应力情况的研究。明尼苏达大学的研究者将气球的形状建模成一个非线性微分方程系统,这个非线性方程系统的解被称为Σ形状。文献[12]使用该模型做了大量的数值计算,这些方程的边界条件是基于有效载荷、气球膜重量、体积和漂浮高度等。文献[13]使用“平行打靶法”求解上升阶段中对称的自然形气球非线性几何方程,该方法假设气球由圆锥体和一个固定角组合而成,并且气球蒙皮上没有周向应力,证明了“平行打靶法”可以很好地求解Σ形状等式。文献[14]构造了“切向增量法”,将气球的加强头部层考虑进模型,忽略蒙皮的弹性形变和褶皱,成功地预测了不对称气球在漂浮阶段的形状,与“平行打靶法”的结果很好地吻合。
对于气球形状的研究,Frank baginski提出气球系统的能量最小并且满足材料的约束,通过这种方法得到的气球形状叫做EM形状(Energy Minimizing Shape)[15]。文献[15-16]根据气球系统的能量最小化原理,将气球实际观察中的特征(如褶皱等)考虑进模型,对上升阶段高空气球的轴对称形状、非对称形状进行建模,模型的计算结果能够很好地反映气球形状,并且还利用“差分原理”计算气球形状,发现该方法计算的对称EM形状与求解标准Σ形状能很好地吻合;而对于不对称形状气球,该方法计算出的气球形状与实际观察中出现的气球形状特征很接近。文献[17]基于壳体有限元法对科学气球进行结构分析,分析了科学气球不同飞行高度下外形和蒙皮应力分布情况。
国内方面,文献[18]通过推导考虑多种因素的一般球形理论得到了地面不同充气体积下球体的二维形状,对不同因素在球形设计过程中的影响进行了详细的分析,并设计了地面试验验证气球形变和应力分析数值结果。文献[19]采用有限元方法,通过选择适当的单元算法、接触算法和流固耦合参数,初步给出了半充气自然形球体形状。文献[20]通过考虑大气环境因素和浮升气体温度的影响,简单预测了气球在地面和漂浮高度的几何外形和蒙皮张力。文献[21]利用肥皂泡理论分析气球膨胀的全过程,通过最小能量理论进行应力分析和剪裁设计,对气球不断上升过程中体积扩大、增加内压过程进行研究,分析其形状变化和膜应力变化特征。
自然形高空气球在上升过程中体积随上升高度的增加而变化,这是由于外界大气温度、密度和压力随上升高度的增加而变化,气球受到的热辐射影响气球内浮升气体的温度,导致气球内浮升气体压力的变化和气球膜内外压差的变化,气球的几何外形随压差的变化而改变。实际上,气球的蒙皮应力由气球的曲率半径决定,因此需要准确且可靠的理论方法来预测气球上升过程的蒙皮应力,本文考虑气球在上升过程中的热辐射,利用最小势能法通过数值迭代计算了自然形气球在上升过程中的形状和应力情况,研究了浮升气体充气量、气球内外温差对气球形状和应力分布的影响。该方法简洁方便,且可获得较为精确的预测结果,为高空气球的工程应用及概念设计等问题奠定基础。
1 理论模型
1.1 气球热力学模型
根据热力学方程,气球内部浮升气体的体积及压力都受到气体温度的影响。为了研究高空气球形状以及蒙皮应力状况,有必要针对高空气球的热特性进行分析。高空气球在升空过程中,外部受气体对流、太阳辐照、地面红外辐射等多种环境热流因素的影响,内部受蒙皮内表面间的辐射换热、表面自然对流换热等因素影响[22],内、外热环境通过蒙皮进行耦合换热,引起气球温度场的瞬态非均匀变化。本文在分析平流层热环境的基础上,考虑高空气球内部浮升气体温度受多种辐射热源以及表面对流等复杂因素影响[23],建立了高空气球的热力学模型,研究了浮升气体的热性能。
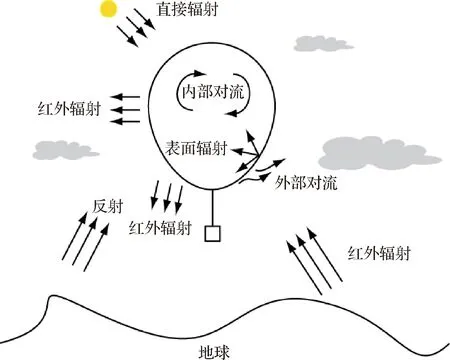
图1 高空气球热环境因素Fig.1 Thermal environment of the high altitude balloon
高空气球的各个部分受到不均匀的太阳辐射,将气球蒙皮划分成小网格,由N个灰体表面组成封闭系统,则蒙皮单元的稳态平衡方程为:
qout,ab-qout,em+qin,ab-qin,em+qcv,ex+qcv,in=0
(1)
式中:qout,ab为蒙皮单元外表面吸收的辐射热流,qout,em为蒙皮单元外表面发射的辐射热流,qin,ab为蒙皮单元内表面吸收的辐射热流,qin,em为蒙皮单元内表面发射的辐射热流,qcv,ex为蒙皮单元外部对流,qcv,in为蒙皮单元内部对流。
蒙皮单元外表面吸收的辐射热流qout,ab=qs+qAlb+qAms+qIR,e。其中,太阳直接辐射热流qs为:
qs=αsτsEscosβ
(2)
式中:αs为蒙皮外表面对太阳光的吸收率,τs为大气对太阳辐射的透射率,Es为太阳常数,取值1358 W/m2[8],β为蒙皮单元外法线与太阳光线的夹角[24]。
大气对太阳辐射的透射率τs为:
τs=(e-0.65ν+e-0.95ν)/2
(3)
式中:ν为空气质量比。
反照辐射热流qAlb为:
qAlb=σfρeIAlbsinθ
(4)
式中:σf为指示因子,白天取值为1,夜晚取值为0,ρe是地球反照率,IAlb为地面反射辐射强度,具体计算见文献[25],θ为光线与地平线的夹角。
大气散射辐射热流qAms为:
(5)
式中:α为太阳高度角,φ为蒙皮面单元法向量与重力方向的夹角[25]。
地球红外辐射热流qIR,e为:
qIR,e=αexτairqeFw,e
(6)
式中:αex为蒙皮外表面红外辐射吸收率,与蒙皮外表面的发射率相等,τair为空气红外透射率,qe为地球红外辐射热流,取值为220 W/m2[24],Fw,e为蒙皮表面对地球的角系数。
蒙皮单元外表面发射的辐射热流qout,em为:
(7)
式中:εex为蒙皮外表面发射率,σ为波尔茨曼常数[25],Tair为外界大气温度,εsky为天空发射率,具体计算见文献[22]。
对于蒙皮内表面单元i,其发射的辐射热流qin,em为:
(8)
式中:εin为蒙皮内表面发射率,Xi,j为微元面i对微元面j的角系数,见参考文献[26],qin-j,em为蒙皮内表面单元j发射的辐射热流。
蒙皮单元内表面吸收的辐射热流qin,ab为:
(9)
蒙皮单元外部对流qcv,ex为:
qcv,ex=hex(Tair-Tfilm)
(10)
蒙皮单元内部对流qcv,in为:
qcv,in=hin(Tgas-Tfilm)
(11)
式中:hex为该蒙皮单元外表面与气流的对流换热系数,hin为该蒙皮单元内表面与高空气球内部浮升气体的自然对流换热系数,Tgas为高空气球内部浮升气体温度。
蒙皮单元外表面与气流的对流换热系数hex为[24]:
(12)
式中:Re为雷诺数,Prair为空气普朗特数,λair为空气导热系数,L为高空气球特征长度。
蒙皮单元内表面与高空气球内部浮升气体的自然对流换热系数hin为[25]:
hin=C(Gr·Prgas)nλgas/L
(13)
式中:C,n为常数[25],Gr为格拉晓夫数,Prgas为浮升气体普朗特数,λgas为浮升气体导热系数。
(14)
式中:ρgas为浮升气体密度,g为重力加速度,μgas为浮升气体动力黏度,R0为气球半径。
高空气球内部浮升气体平均温度Tgas的控制方程为:
(15)
式中:cgas是浮升气体的比热容,Mgas是浮升气体的质量,S为气球整个表面,dA是高空气球蒙皮单元面积。
1.2 气球几何外形
由于气球囊体材料具有非线性、黏弹性、各向异性和不能抗压等特点[27],当气球部分填充浮升气体时,气球的底部形成复杂的非轴对称的褶皱部分,而对于气球上部分,基本呈轴对称形式[14]。在之前的气球研究中,自然形气球研究普遍采用的优化方案是基于以下假设[18]:(1)关于中心轴轴对称;(2)圆周应力为零;(3)蒙皮材料不能伸长。本文对于自然形气球采取上述假设(1)和(3),对于在没有携带载荷情况下的轴对称气球,它的几何形状可以看成一个半径为R0,球心为C0的球体;而当气球在携带载荷的情况下,气球趋于一个球-圆锥体,由球体与圆锥体相切组成[20],如图2所示。
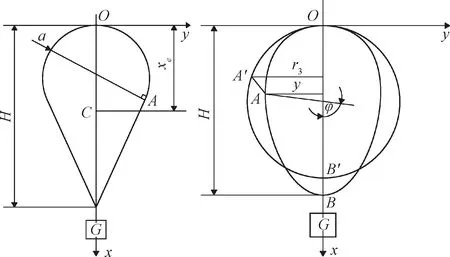
图2 气球坐标示意图[23]Fig.2 Balloon coordinate diagram
可以将气球的剖面曲线写为:

(16)
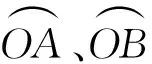
因此,在经向方向材料约束方程写为:
(17)
(18)
同时还有几何关系:
(19)
将气球剖面曲线代入到材料的约束方程(17)、(18),就能得出切点A的位置yA,xA,气球质心的位置xC,气球的竖直方向的总长度H,以及上半部分球的半径a,从而得到气球的体积为:
(20)
1.3 最小势能法
最小势能原理是指在所有可能的变形中,其实际存在的变形使得物体的总势能取最小值[28]。气球系统的总势能由两部分组成,一部分是气球系统的重力势能,另一部分是浮升气体的压力势能。
通过简化模型,气球系统的重力势能由浮升气体的质量,气球蒙皮的质量以及携带载荷的质量产生,表达式为:
E=-(Mgas+m0)gxC-mGgH
(21)
式中:m0为气球蒙皮的质量,mG为气球携带载荷的质量;xC为气球系统的质心的坐标。
根据气球系统的受力平衡,就能得到浮升气体的质量:
Mgas=Vρ-(m0+mG)
(22)
式中:ρ为外界大气的密度。
浮升气体的压力势能表达式为:
W=Δp·V·lnV
(23)
其中,Δp为球内外的压差,根据理想气体状态方程,可以得到Δp为
(24)
式中:Rmix为浮升气体常数,p2为气球外部大气压强。
气球系统的总势能为:
Π=W+E=Δp·V·lnV-
((Mgas+m0)gxC+mGgH)
(25)
将气球的几何外形方程求得的参数代入到总势能方程中,这样式(25)就是关于参数c的表达式,通过求得总势能的最小值,就能解得参数c,求得相应的气球剖面曲线,就能得到不同高度的气球形状。
1.4 蒙皮应力
通过简化模型,不考虑气球在上升过程中出现的褶皱、多余材料等造成气球水平剖面半径变化,气球需要满足材料在圆周方向的约束。应力分布情况如图3所示。
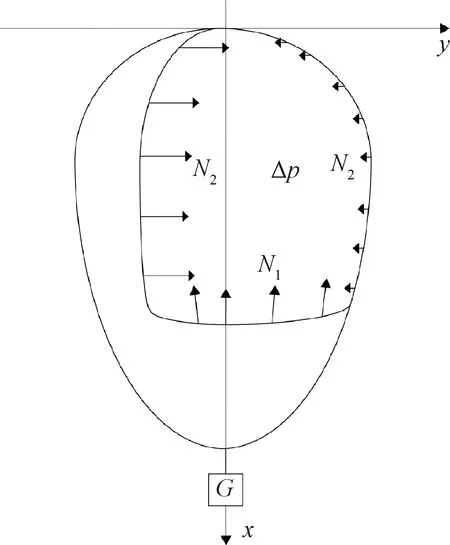
图3 气球应力示意图Fig.3 Balloon stress schematic
因此,经向应力N1的平衡方程为:
2πr3N1sinφ=Δpπy2+G
(26)
2πr3是气球在没有承受载荷时水平剖面周长,G为气球竖直方向的重力。简化方程(26),得到:
(27)
同理,分析气球竖直剖面,气球的纬向应力N2为:
(28)
故经向应力N1、纬向应力N2为关于y,r3和φ的表达式,y和r3的关系由材料的经向约束方程(17)、(18)得到,因此,只要求得气球的形状就能得到气球的经向应力和纬向应力。
2 算例结果与分析
2.1 计算实例
由上述所建立的模型,编写高空气球上升过程的数值仿真程序,整个仿真程序的结构如图4所示。本文所用的高空气球规格参数,基本参数见表1[20]。
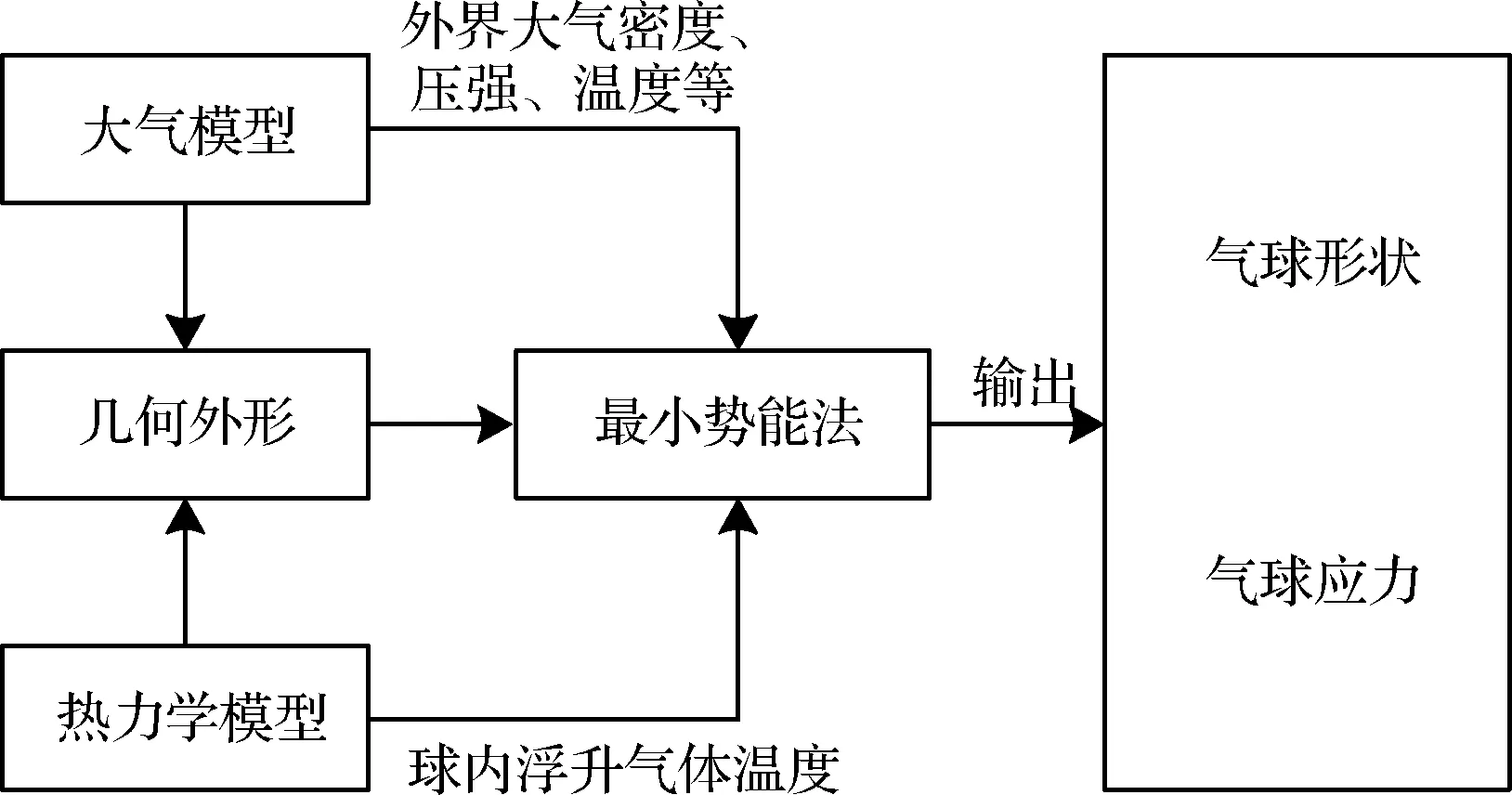
图4 仿真程序结构图Fig.4 Simulation program structure
表1 气球系统参数[20]
Table 1 Balloon system parameters

参数值气球初始半径R0/m17.5氦气气体常数Rmix/(J·kg-1·K-1)1511.4载荷重量G/N10520气球蒙皮重量m0g/N4618 气球蒙皮厚度/mm0.12 蒙皮面密度/(g·m-2)120
2.2 仿真结果
2.2.1模型校验
为了校验以上提出的高空气球热力学模型,将仿真结果与文献[25]中的结果进行对比,采用文献[25]中的超压气球物性参数,分析气球在抵达31.5 km左右高度时的内部浮升气体温度变化,可以得到图5。上午6时之前氦气温度维持在240 K左右,随后开始上升,中午12时达到最大,随即下降,该模型计算结果与对比值最大相差0.5 %,与文献[25]中结果吻合较好。
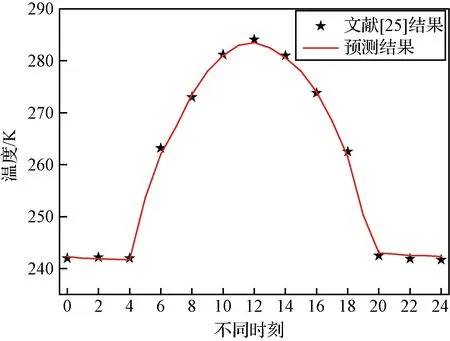
图5 不同时刻氦气平均温度Fig.5 Average temperature of the helium at different times
选用Wen等[14]所设计的气球的参数,利用最小势能法和文献中所计算的应力情况进行对比,验证简化几何模型下的最小势能法结果的准确性。

表2 气球参数[14]Table 2 Balloon parameters
图6展示了利用表2气球参数经过最小势能法计算气球的应力情况与文献[14]的结果进行对比,文献[14]选取浮力系数为0.06,利用最小势能法得到的气球经向应力N1可以吻合文献[14]的计算结果。
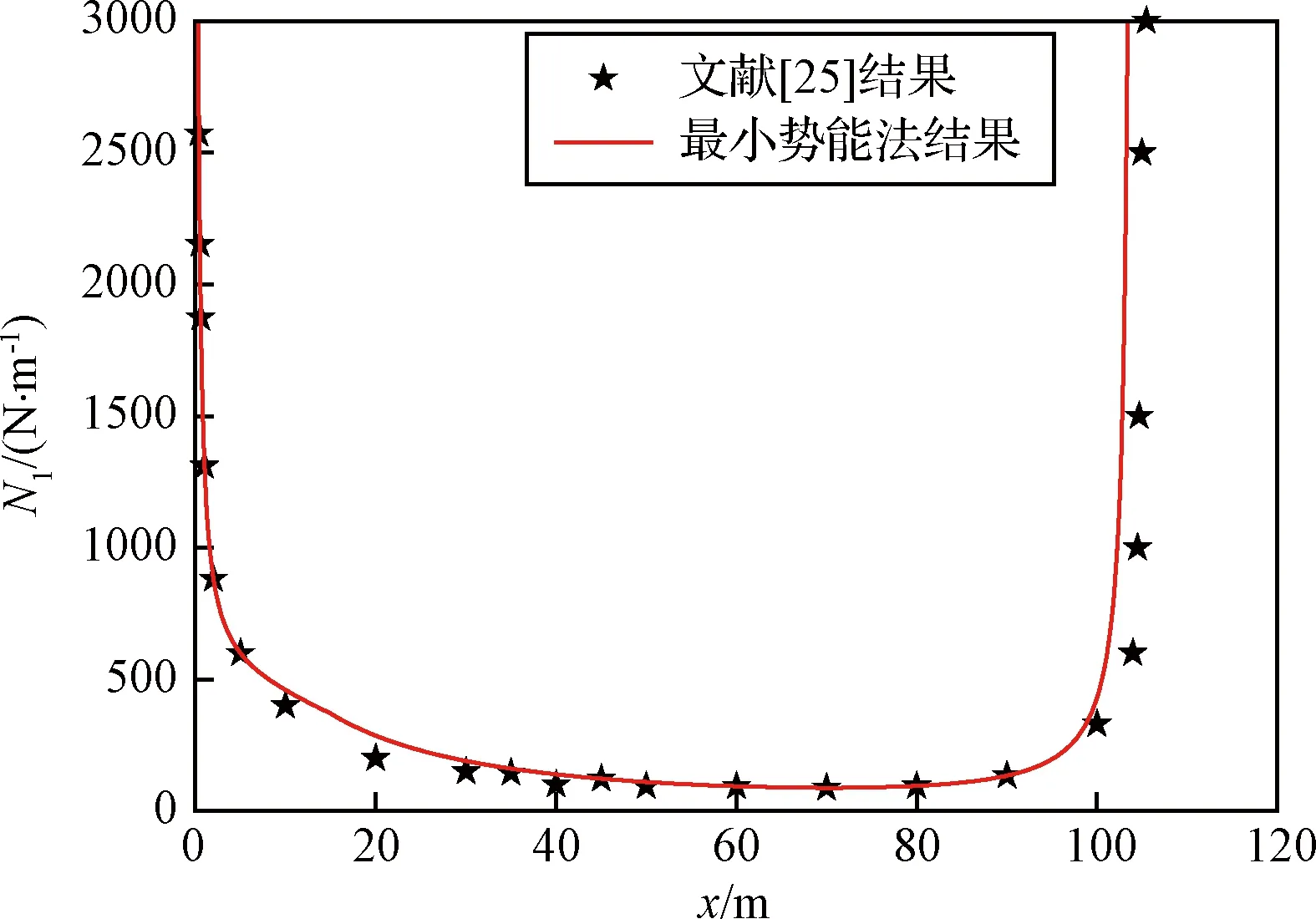
图6 蒙皮应力对比图Fig.6 Comparison of film stress
2.2.2上升过程气球形状及应力
将气球参数代入到气球热力学模型中,可得到气球在上升过程中不同高度的内部氦气温度Tgas,再将气球系统的各项参数代入到气球总势能表达式(25)中,通过求气球总势能的最小值,得到气球上升过程中不同的c值,确定气球上升过程中的形状及应力。图7是气球在上升过程中的形状,随着高度的增加,c值逐渐增大,气球下部分的圆锥体的母线越来越平缓,气球由开始的水滴形逐渐变化成球形。
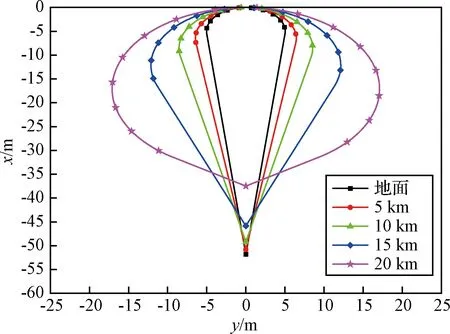
图7 不同高度气球形状图Fig.7 The balloon shape at different height
图8是上升过程中蒙皮的经向应力N1的变化曲线。图9是上升过程中蒙皮的纬向应力N2的变化曲线。经向应力N1比纬向应力N2的数量级大,因此,很多自然形气球的应力分析时忽略纬向应力。经向应力N1呈现“马鞍”形,气球的顶部和气球的底部经向应力与气球中间部分的经向应力相差很大,在现在的气球设计过程中,气球顶部和气球底部都加多层蒙皮材料来承受气球的经向应力;气球的纬向应力N2与经向应力N1分布不同,气球的纬向应力N2的极值在气球的半径最大处,并且数值很小,在上升过程中随高度的增加,纬向应力N2逐渐减小。
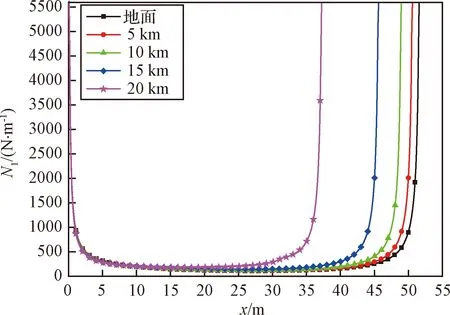
图8 上升过程气球经向应力图Fig.8 Balloon meridional direction stress curves duringthe ascent
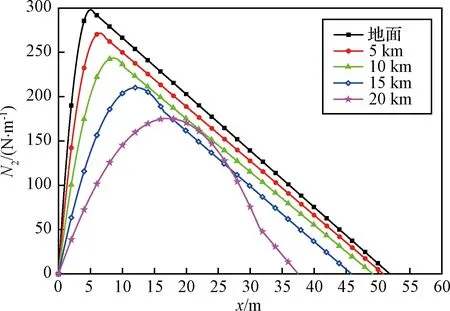
图9 上升过程气球纬向应力图Fig.9 Balloon circumferential direction stress curvesduring the ascent
2.2.3不同充气量的气球形状及应力分布
选取气球在03:00时的准稳态计算气球在不同充气量下气球形状和经向应力N1的分布情况,气球的充气量由气球所携带的载荷决定,本文选取相差200 kg的5个载荷量,为252~1052 kg之间,分析在20 km漂浮下气球的形状及经向应力N1分布情况,如图10、图11所示。
图10是气球在不同充气量下20 km气球的形状,随着气球携带载荷量的增加,气球上半部分圆球体的半径a变大,而气球整个竖直长度H变小,而出现变化的位置位于圆球体与圆锥体相切点,携带载荷量大的气球下部分的圆锥母线斜率较小,导致气球竖直长度H变小,携带载荷量小的气球下部分的圆锥母线斜率较大,导致气球竖直长度H变大。
图11是气球在不同充气量下20 km的经向应力N1分布情况,在不同的充气量下,经向应力N1服从“马鞍”形分布,在气球的顶部和气球的底部较大,气球中间部分数值较小,在本文选取的充气量中,气球的顶部部分应力大小基本相同,而区别出现在气球的底部,气球的经向应力N1急剧上升到最大,且底部的最大值与气球携带的载荷量的大小有关,载荷越大,气球底部的应力值越大,气球膨胀得越厉害,气球容易破裂。
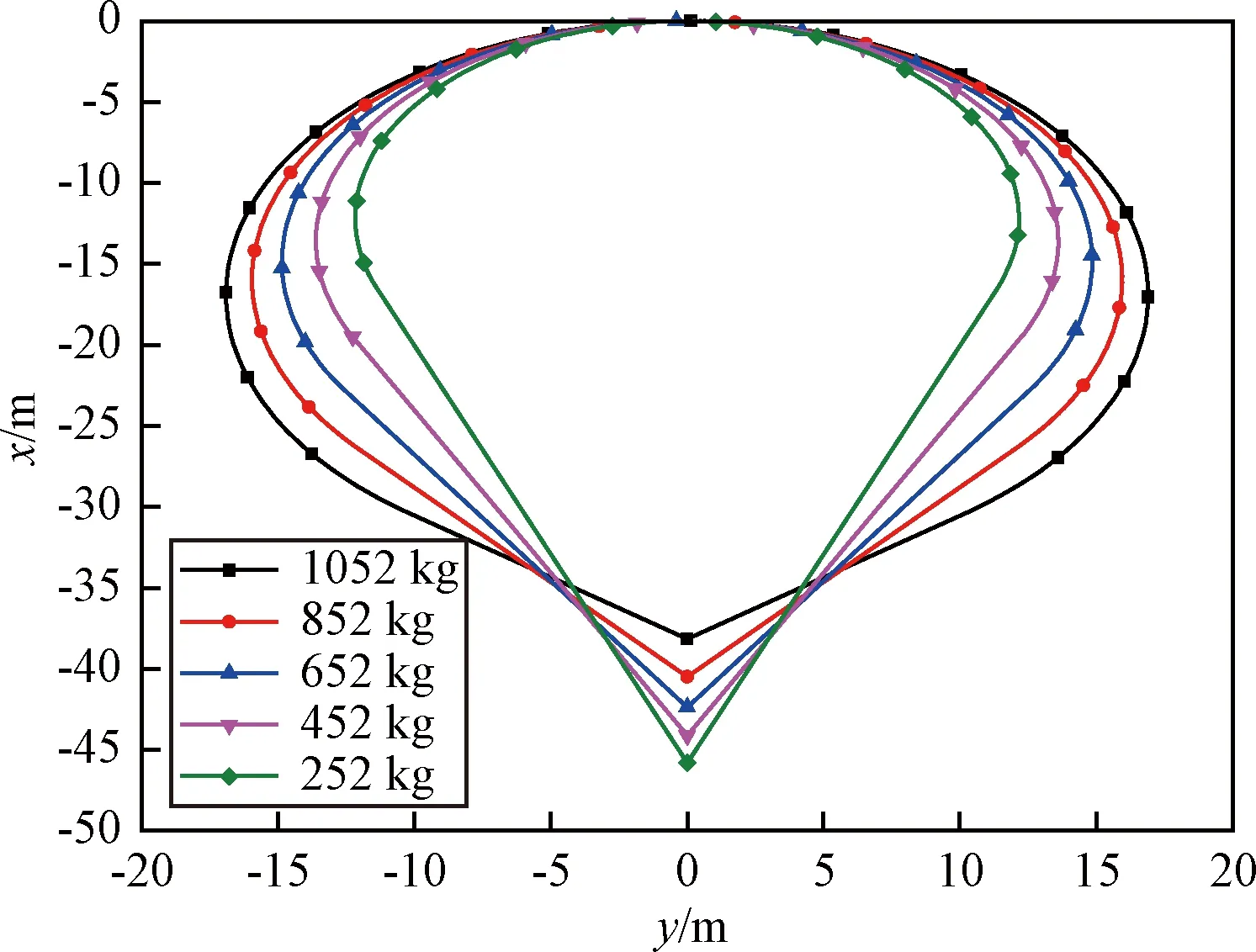
图10 不同载荷量下气球形状图(20 km)Fig.10 Balloon shape under different load (20 km)
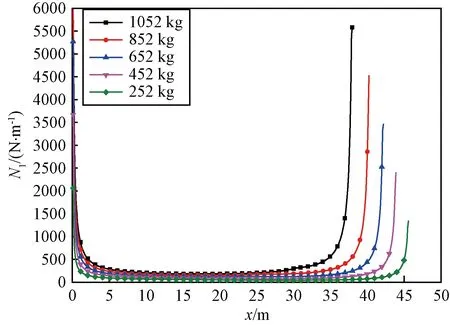
图11 不同载荷量下气球经向应力图(20 km)Fig.11 Balloon meridional direction stress curves underdifferent load (20 km)
2.2.4不同时刻的气球形状及应力分布
选取气球携载1052 kg在不同的时刻下计算气球在20 km的形状及应力分布,在不同的时刻下根据热力学模型计算得到球内外温差,球内外温差的不同导致球内外压差的不同,压差使得气球的形状及应力分布规律不同。
图12是不同时刻下20 km气球形状图,在20 km高度时,气球内外温差受太阳辐射影响随时刻变化,气球形状也随温差发生变化,温差越小,气球越圆,呈球形;图13是不同时刻下20 km气球经向应力N1分布情况,在20 km不同时刻下,气球顶部和中部经向应力N1大致重合,在气球的底部经向应力N1出现不同。

图12 不同时刻下气球形状图(20 km)Fig.12 Balloon shape at different times(20 km)
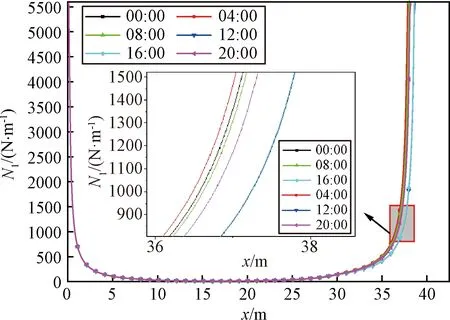
图13 不同时刻下气球经向应力图(20 km)Fig.13 Balloon meridional direction stress curves atdifferent times(20 km)
3 结 论
本文建立了自然形高空气球的热力学模型和几何模型,采用最小势能法对自然形高空气球上升过程的形状和应力进行仿真研究,还比较了不同充气量、不同时刻下气球形状及应力分布情况,得出相关结论,为气球设计及工程应用中初步判断气球的形状及应力情况提供了一种较为有效的计算方法。
1)自然形高空气球在上升过程中由于外界环境的变化导致气球内外压差的变化,气球的体积不断变大,气球的竖直长度逐渐减小,气球的形状也逐渐变成“圆球”形;气球的经向应力不断增大,纬向应力逐渐减小。
2)自然形气球的经向应力分布呈“马鞍”形,极值分布在气球顶部和气球底部,并且数量级较大;而纬向应力极值分布在气球半径最大处,数值较小,因此纬向应力对自然形高空气球的影响较小,可以忽略。 3)不同充气量下,在气球的顶部和气球的底部较大,气球中间部分数值较小,而区别出现在气球的底部,载荷越大,气球底部的极值越大,气球容易破裂;而不同时刻工况下,气球在20 km处形状及应力受不同时刻的影响较小。

