组合动力运载器上升段轨迹智能优化方法

周宏宇，王小刚，赵亚丽，崔乃刚

(1. 哈尔滨工业大学航天学院，哈尔滨 150001；2. 北京航天晨信科技有限公司，北京 102308)

0 引 言

现代航天活动正朝着多元化、频繁化的方向发展；在这种背景下，传统的一次性航天运载工具面临着发射成本高、安全性低、准备时间长等问题，制约了航天事业的发展。因此，世界各航天强国始终在研究更先进、更便捷的航天运载器，其中最具代表性的便是基于吸气式组合动力的水平起降可重复使用运载器[1-3]。20世纪末，日本率先提出了一种将变循环涡扇发动机和冲压发动机组合的方案，证明了其用于天地往返运输的可行性。2016年，美国公布了基于“协同吸气式火箭发动机”的两级入轨方案；同年，中国披露了正在研制的组合动力运载器项目，计划在2030年实现亚轨道应用；在2017全球航天探索大会上，中国宣布正在研发水平起降天地往返运载器，现已完成多项关键技术的地面试验。世界各国的诸多举动表明，基于吸气式组合动力的水平起飞两级入轨方案已成为发展可重复使用运载器的重要方向[4-6]。

设计上升段轨迹是可重复使用运载器执行任务的首要步骤。但对于采用组合动力完成水平起飞、爬升加速的运载器来说，其动力、气动、轨迹和指标间有着很强的相互制约关系，并且不同动力模态对飞行状态和环境约束有着不同的需求[7]。因此，上升段轨迹优化面临着约束条件严苛、动力切换频繁、性能指标与设计变量间映射关系复杂等问题，求解上升段轨迹优化问题面临着极大的挑战。多年来，许多学者针对水平起飞运载器的上升段轨迹优化问题展开了研究。早期主要是借助简化数学模型解决这类优化问题，例如Corban等[8]利用近似线性模型简化了高度和速度的微分方程，降低了轨迹设计的难度。随着最优控制理论的发展，开始考虑更符合客观规律的数学模型。Lu等[9]指出，吸气式动力运载器的爬升轨迹优化问题可转化为典型两点边值问题求解。Murillo等[10]将优化问题转化为一个多项式方程求根问题，进而提出了一种上升段轨迹快速优化方法。Pan等[11]通过简化协态方程降低了间接法的求解难度，同时借助多重打靶法实现了初值的快速生成。陶超[12]用Gauss伪谱法求解了高超声速飞行器最优上升段轨迹。龚春林等[13]针对吸气式动力工作模态多、冲压模态约束条件复杂的问题，利用Radau伪谱法建立了基于混合积分变量的轨迹优化模型，有效处理了运载器多段飞行约束条件。窦立谦等[14]将Gauss伪谱法和(Sequence quadratic program)SQP相结合，求解了考虑密度、声速和发动机推力变化及地球引力等因素的燃料最优爬升轨迹。李惠峰等[15]基于有限差分方法和改进牛顿法，设计了一种以参考面积为同伦参数的迭代方法，同时以近似解析解为初值，实现了吸气式运载器上升轨迹的快速优化。

现有文献有效解决了组合动力运载器的上升段轨迹优化问题，但这些研究通常只关注临近空间中的高超声速爬升/巡航段，鲜有关注从起飞至进入稀薄大气的完整爬升轨迹。当针对跨大空域/速域的完整上升段轨迹进行设计时，必须考虑整合多种动力模态的多组合动力系统(如涡轮基冲压发动机(TBCC)+火箭基冲压发动机(RBCC))，涉及更多的轨迹分段、约束条件、耦合因素和优化变量，优化问题的非线性将更强；而现有文献难以在满足诸多约束条件下获得最佳的多组合动力使用方式和上升段轨迹。

为解决上述问题，针对上升段中动力、状态和指标间的复杂耦合关系以及动力系统对飞行环境提出的复杂约束条件，设计了一种全新的考虑多重动力切换的攻角剖面，并将上升段轨迹优化问题转化为多参数寻优问题。基于该剖面进行推导，得到了攻角及其变化率的极值与优化参数间的解析映射关系，大幅简化了优化算法需要处理的约束条件，同时自然满足轨迹的平滑性要求。然后，提出了一种改进的PSO算法用于求解最优轨迹：以粒子收敛性分析为基础，以粒子空间散布状态和收敛时间为参考，以燃料最优为指标，引入DDPG(Deep deterministic policy gradient)强化学习方法对影响PSO计算效率的关键参数进行动态调整；随着PSO迭代信息的积累和粒子群向最优解的逐渐聚集，DDPG能够智能、准确、快速地输出PSO算法控制参数，进而提高算法计算性能。仿真结果表明，本文提出的优化方法能够有效解决运载器上升段轨迹优化问题；相对其它PSO算法，结合强化学习的改进PSO算法在计算效率上有明显提升。

1 组合动力运载器运动数学模型

1.1 总体参数模型

借鉴日本“HYPR”计划中提出的“将变循环涡扇发动机和冲压发动机组合”方案，本文研究的运载器先后在TBCC和RBCC的作用下飞行。通过分析TBCC和RBCC的固有特点和工作模态，可根据热力学原理建立组合动力发动机性能计算模型。

1)TBCC性能计算

TBCC动力包含涡轮和冲压两种模态。采用涡轮风扇发动机作为TBCC的涡轮部分，同时采用“设计点分段定比热气动热力计算”方式，建立涡轮发动机性能计算模型；结合气流路径和部件间能量守恒关系，可得涡轮发动机的推力和比冲为[16]：

(1)

式中：Wa,tb为进入涡轮发动机的空气质量流量，Fs,tb为推力/流量比，msfs为发动机耗油率，g为重力加速度。Wa,tb=ρc0Stb，其中ρ为环境大气密度，Stb为涡轮发动机进气道入口面积，c0为进气道入口气流速度；Fs,tb和msfs的计算方式见文献[16]。

考虑压缩、加热、绝热膨胀和放热四个过程，TBCC冲压发动机的推力和比冲分别为[16]：

(2)

式中：ηf为冲压发动机总效率，Hu为燃油热值，fsc为油气比，Wa,sc为进入冲压发动机的空气质量流量。类似的，有Wa,sc=ρc0Ssc，其中Ssc为冲压发动机进气道入口面积。

2)RBCC性能计算

设计RBCC发动机的性能为马赫数的函数。一般来说，当切换至RBCC时马赫数已超过3.0，因此仅关注RBCC亚燃冲压及以后的工作模态。

亚燃/超燃冲压模态下的推力和比冲分别为：

(3)

(4)

式中：m0为运载器起始质量，Ma为马赫数。

纯火箭模态下的推力和比冲分别为[16]：

(5)

综上，动力系统的待优化参数如表1所示[16]。

3)气动模型

认为气动系数受攻角和马赫数的影响，通过相关气动参数拟合，同时参考类似高超声速飞行器的气动特性，给出如下运载器的气动参数模型：

(6)

式中：cD为阻力系数，cL为升力系数，α为攻角。

表1 组合动力发动机待优化参数Table 1 Optimization parameters for combined-cycle-basedengine

1.2 运载器上升段运动模型

纵向剖面内的运载器上升段运动模型为[14]：

(7)

式中：V为飞行速度，γ为飞行路径角，r为运载器质心到地心的距离，m为运载器质量，Tm为推力，Isp为比冲，D为气动阻力，L为气动升力，g为重力加速度。

气动力的计算方式如下：

(8)

式中：q=ρV2/2为飞行动压，Sm为特征面积。

1.3 上升段轨迹优化模型

首先，设置终端约束条件如下：

(9)

考虑结构强度和防热等因素，取过程约束为：

(10)

式中：qmax为允许的最大动压，Nm为法向过载，Nm,max为允许的最大法向过载。

另外，不同于采用火箭发动机，吸气式发动机对飞行攻角有着很严格的约束需求，并且组合动力中不同模态对飞行攻角的约束也各不相同。因此，针对各动力模态，分别建立不同的攻角约束：

(11)

式中：αmax,1和αmin,1分别为TBCC涡轮工作状态下的攻角上/下限，αmax,2和αmin,2分别为TBCC冲压工作状态下的攻角上/下限，αmax,3和αmin,3分别为RBCC亚/超燃冲压状态下的攻角上/下限，αmax,4和αmin,4分别为RBCC火箭模态下的攻角上/下限；Maq3为RBCC进入火箭模态时的马赫数，|dα/dt|max为允许的最大攻角变化率。

最后，将上升段轨迹优化问题的性能指标取为燃料最省，即minJ=(m0-mf)/m0。

2 上升段攻角剖面设计

通过设计攻角—速度剖面完成上升段轨迹设计；根据动力形式(TBCC涡轮、TBCC冲压和RBCC)将攻角剖面分为三段，即将攻角设计为速度的分段多项式函数：

α(V)=

(12)

式中：V0为初始速度，Vq1和Vq2分别对应Maq1和Maq2；ai(i=0,1,…,n1)，bi(i=0,1,…,n2)和ci(i=0,1,…,n3)为待定系数，共(n1+n2+n3+3)个。

取n1=n2=n3=3，即用三次多项式描述各动力段的攻角，因此共12个未知系数。相应的攻角剖面示意图见如图1，其中V1,0=V0，V2,0=Vq1，V3,0=Vq2，V4,0=VE=Vf。

为求解这12个未知系数，需要建立12个方程。首先，为保证攻角及其变化率在Vq1和Vq2处的连续性，需满足以下条件：

(13)

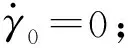
(14)

(15)

(16)

式中：V1,1=V1,0+(Vq1-V1,0)/3，V1,2=Vq1-(Vq1-V1,0)/3，V2,1=(Vq1+Vq2)/2，V3,1=(Vf+Vq2)/2。

图1 攻角-速度剖面Fig.1 Ascent profile of angle-of-attack (AOA) and velocity

因此，上升段剖面的设计变量为：

U1=[α1,1,α1,2,α2,0,α2,1,α3,0,α3,1,α3,3]T

(17)

同时，发动机待优化参数为：

U2=[πCL,πCH,T3,Maq1,Maq2]T

(18)

由优化约束模型可知，上升段对攻角提出的约束最为复杂，若能将攻角约束在优化计算前解决，则能够大大减少优化算法的计算量。

对于三阶多项式，以区间[V0,Vq1]为例，攻角的表达式为：

(19)

对式(19)求导可得：

(20)

因此：

(21)

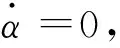
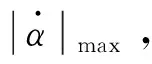
(22)

由式(21)可得：

(23)

(24)

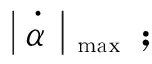
(25)

式中：εh是相对hE而言很小的量。

3 上升段攻角剖面优化算法

3.1 PSO算法收敛性分析

PSO算法中每个粒子都代表优化问题的一个潜在解，对应的性能指标称为“适应度”。设Mpso个粒子在空间中搜索Dpso个参数，则第i(i=1,2,…,Mpso)个粒子在Dpso维搜索空间中的位置矢量和速度矢量分别为：

(26)

记第i个粒子迄今找到的最佳位置为Pi，Pi对应的适应度为pbest；同时记所有粒子搜索到的最佳位置为Pg，Pg对应的适应度为gbest。

(27)

PSO算法中，整个群体按照如下方式进化[17]：

(28)

(29)

定义φ1=c1r1+c2r2，φ2=c1r1pi,j+c2r2pg,j，由PSO算法进化公式可得：

(30)

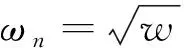
设pi,j和pg,j为常值，分别记为p和g。用符号E表示某变量的期望，则根据式(30)可得：

(31)

(32)

当φ1-w-1>0时，粒子在第j维空间中将渐进收敛于(p+g)/2。设算法在相对误差小于2%时收敛，记收敛时间为ts，则有：

1)当0<ξn<1时，式(30)是一个欠阻尼系统，收敛时间为：

(33)

2)由于φ1具有随机性，故ξn=1一般不会出现。

3)当ξn>1时，式(30)是一个过阻尼系统，收敛时间为：

(34)

PSO算法中通常取c1=c2=2.0，因此ћE(φ1)=2，其中ћE(·)表示某变量的期望；取φ1=2，结合式(33)～(34)并用w取代ξn和ωn，得到收敛时间与惯性权重的关系如图2所示。在此指出，粒子运动是以迭代次数来描述的，故图2中显示的并非实际时间，仅为收敛性分析提供参考。

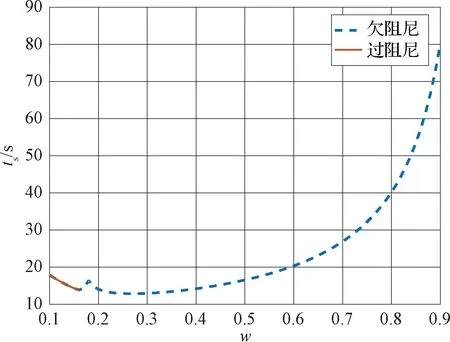
图2 收敛时间与惯性权重的关系Fig.2 The relation between convergence time and weight

3.2 基于强化学习的改进PSO算法

由图2和式(33)可知，粒子的收敛过程主要由频率和阻尼决定，而频率和阻尼又由惯性权重、随机数r1和r2以及学习因子决定。因此，只需根据r1和r2动态调整w，c1和c2，即可实现对PSO收敛过程进行控制。然而，以线性权重、随机权重、指数权重和固定权重为代表的诸多现有研究成果表明，依靠惯性权重对PSO算法的搜索过程进行准确控制是很难实现的，这不仅需要设计者对研究问题的深入了解，还依赖于大量的仿真实验分析[18]。

设Ulearn=[w,c1,c2]T，为了获得最佳Ulearn，借助强化学习方法[19]，通过构建策略网络对PSO进化过程的智能控制，即在每一代进化中输出最优Ulearn值，进而实现对PSO算法收敛过程的动态智能控制，提高PSO算法性能。

强化学习的基本过程如下：

1)环境给智能体一个观测值。

2)智能体收到观测值后做出一个动作。

3)环境收到动作后做出一系列反应，如对智能体的动作给予一个奖励或给出新的观测值。

在PSO算法中，观测值定义为表征粒子空间散布状态的向量；动作空间为3维，分别对应对w，c1和c2的更新，且动作为连续值。

(35)

式中：n1，n2和n3为事先设定的超参数。

2)奖励(记为r)：奖励为一个反馈信号，表明当前动作的优劣；取gbest作为奖励值。

3)状态(记为s)：环境状态转移根据式(30)完成，每次进化后重新计算粒子的空间散布状态信息。

基于DDPG强化学习算法调整Ulearn。DDPG框架如下：

1)值函数网络Qnet：表征某环境状态下某一动作对应的价值函数，输入为[s,d]。

2)策略函数网络Pnet：输入为s，输出为d，此网络即Ulearn优化求解器。

3)片段：PSO从开始到终止的全过程。

基于DDPG的改进PSO算法设计流程如下：

1)使用权重θQ和θP随机初始化值函数网络Qnet和策略函数网络Pnet。

3)对于PSO算法全过程：

(2)随机初始化粒子位置和Ulearn，获取初始状态空间的观测量。

(3)对于PSO算法中的每一步迭代：

①根据当前策略网络选择动作d=P(s|θP)+。

②执行动作d，得到奖励r和新的状态s。

③将状态组(s,d,r,s)保存到经验回放池。

④从经验回放池中NR次随机取样状态组。

⑤计算取样值：

(36)

式中：i=1,2,…,NR，kQ为预先设定的系数。

⑥通过最小化损失函数来更新值函数网络，得到新的θQ：

(37)

⑦使用采样策略梯度更新策略网络：

(38)

⑧定义常系数τθ，更新目标网络：

(39)

图3 强化学习在PSO中的应用Fig.3 The application of reinforcement learning into PSO

经过DDPG大量离线训练后，可得到包含问题模型信息的策略网络，将其作为PSO算法的Ulearn求解器，即可实现基于DDPG的改进PSO算法，如图3所示。PSO算法终止的标准是：达到最大迭代次数或gbest的值在过去3代中变化不超过5%；另外，约束条件借助罚函数法处理[21]。

4 数值仿真及结果分析

首先，设置上升段过程约束为：qmax=400 kPa，Nm,max=6，αmin,1=-5°，αmax,1=15°，αmin,2=-8°，αmax,2=8°，αmin,3=-10°，αmax,3=10°，αmin,4=-10°，αmax,4=10°，|dα/dt|max=8°/s。同时，设运载器起飞质量为60000 kg，其中燃料质量为50000 kg；特征面积为15 m2，TBCC涡轮和冲压发动机的进气道入口面积分别为7.0 m2和6.0 m2；采用液氧/液氢燃料，热值为120.8 MJ/kg。另外，设置PSO算法采用40个粒子，最大迭代次数为20。

建立四个仿真场景从而验证算法的适应性和有效性，相应的上升段初始运动状态和终端状态约束如表2所示。最终，PSO算法在迭代13次后终止，参数优化结果见表3，相应仿真结果见图4～9。

表2 初始状态和终端约束Table 2 The initial states and the terminal constraints

表3 参数优化结果Table 3 The results of parameter optimization

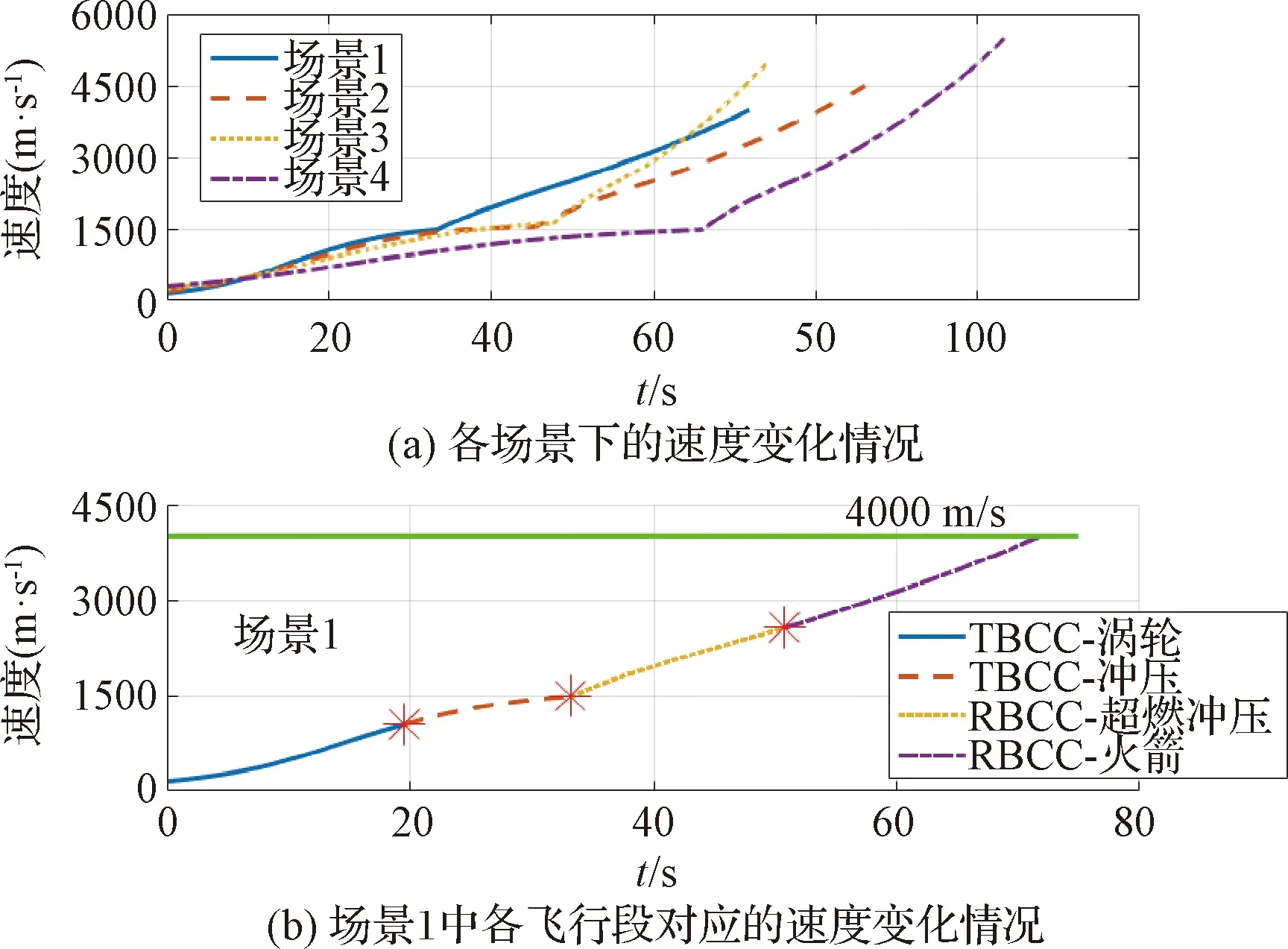
图4 速度随时间变化情况Fig.4 Time histories of velocity

图5 高度随时间变化情况Fig.5 Time histories of altitude

图6 飞行路径角随时间变化情况Fig.6 Time histories of flight path angle

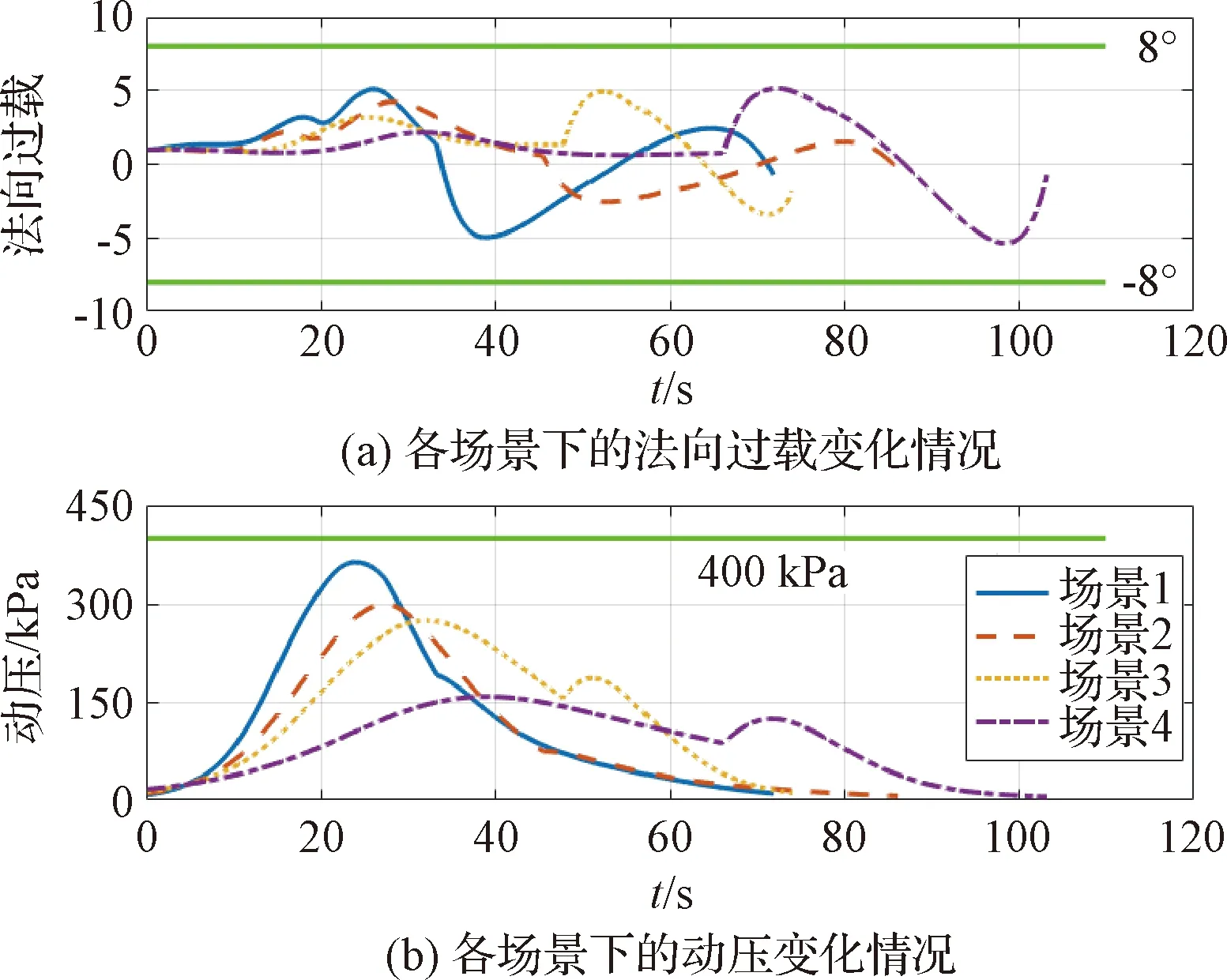
图7 过程约束随时间变化情况Fig.7 Time histories of path constraints

图8 攻角及其变化率随时间变化情况Fig.8 Time histories of AOA and its change rate

图9 攻角及其变化率随时间变化情况(场景1)Fig.9 Time histories of AOA and its change rate (Case1)

从图4～6可以看出，在所有情况下优化算法均能满足上升段终端约束。四种场景下的上升段飞行时间分别为71.8 s、86.1 s、74.0 s和103.3 s。四种场景下的上升段终端飞行路径角分别为14.7°、13.4°、22.1°和14.3°，均满足表2中给出的终端约束条件。图7表明，得到上升段轨迹能满足动压和法向过载约束，其中四种场景下的最大动压分别为363 kPa、301 kPa、275 kPa和158 kPa，最大法向过载(绝对值)分别为5.0、4.2、4.9和5.4。图8表明，上升段攻角曲线十分平滑，攻角变化率始终保持在限定区间内。图9以场景1为例给出了上升段攻角及其变化率的仿真曲线；结果表明，攻角在各动力模态段中均能始终保持在指定的约束范围内，同时根据变化率满足约束条件。

最后，将基本PSO算法(BPSO)和基于高斯扰动的PSO算法(GPSO)[22]与本文提出的基于强化学习的PSO算法QPSO对比，验证QPSO在计算效率上的提升。设三种PSO算法采用相同的约束处理方式，粒子数均为40，最大迭代次数均为20；另外，考虑到PSO算法本身具有随机性，对三种PSO算法均进行50次独立仿真。以表2中的场景1为例，得到仿真结果见表4。仿真结果表明，QPSO搜索到的最优结果和最差结果均优于BPSO和GPSO。从寻优能力来看，QPSO获得的指标较BPSO而言平均高出11.1%，较GPSO而言平均高出6.5%；从计算效率来看，QPSO较BPSO而言平均减少35.3%，较GPSO而言平均减少15.4%。另外，从算法输出稳定性来看(标准差)，QPSO同样优于BPSO和GPSO。综上，本文提出的基于收敛性分析和强化学习的改进策略有效、显著地提升了PSO算法的综合搜索性能。

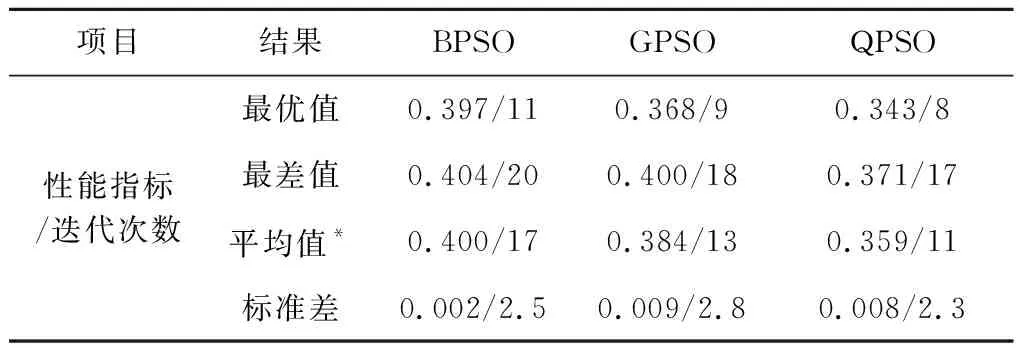
表4 不同PSO算法对比结果(50次独立仿真)

*平均值向上取整

5 结 论

面向未来新一代组合动力水平起飞可重复使用运载器，针对跨大空/速域的完整上升段轨迹优化问题展开深入研究，获得如下成果：

1)考虑多动力模态切换问题，设计了一种新的攻角剖面，通过数学推导解析求解了攻角约束的满足条件，减少了优化算法需要处理的约束数量，降低了优化问题的求解难度。

2)提出了一种改进PSO算法。在收敛性分析的基础上，分析了影响PSO算法寻优过程的关键参数以及这些参数PSO寻优能力间的映射关系。在此基础上，引入强化学习机制对PSO寻优过程进行智能控制，从本质上提升了PSO求解效率。

3)通过多场景数学仿真验证了方法的正确性和有效性，同时通过对比分析验证了改进PSO算法在寻优能力和效率上的提升。