悬臂式电磁发射导轨及壁板在发射状态下的强度分析

何威，魏彦京

(1.燕山大学 建筑工程与力学学院，河北 秦皇岛 066004；2.中国科学院大学，北京 100049)

0 引言

电磁发射器的研究意义极其重大，它将对一个国家的能源、运输、防御和空间规划产生重大影响[1]，因此多年来各国政府对此问题的研究都极为关注。自20世纪80年代以来，电磁发射装置技术的研究取得了多方面进展，应用领域日益广阔。尤其在军事工业方面，经过多年的努力，用于电磁轨道炮的科学技术取得了相当大的进展，并已经在军事应用中进行实践探索，充分体现在电磁轨道炮作战系统的研究。而在达到武器化和实用化前，仍需解决一些工程技术和制造工艺方面的难题[2-4]。其中轨道装置的强度、刚度设计计算是保证发射精度的重要因素。目前，国内外学者对电磁轨道发射装置的力场做了大量的理论分析和计算工作[5]。Tzeng将电磁发射装置轨道简化为弹性基础梁，求解了磁场压力下轨道炮内膛的应变场和应力场[6-8]。Johnson等[9]同样将电磁轨道发射装置的轨道简化为弹性地基梁，运用材料力学的方法进行计算，初步分析了电磁轨道在电磁压力作用下应力波的传递特性。Jin等[10]将电磁炮轨道简化为Bernoulli-Euler梁，研究了电磁炮动态响应，并用数学计算软件MATLAB进行了数值模拟，Che等[11]同样基于Bernoulli-Euler梁理论将电磁炮轨道简化为单层梁，讨论了不同约束及预应力对轨道振动及刚度的影响。Cao等[12]运用Winkler梁模型分析了轨道的变形，而Lee等[13]运用Timoshenko地基梁分析了轨道的动态响应。田振国等[14]将复合电磁炮轨道简化为弹性基础梁，运用二维Fourier变换的方法求得了轨道在动荷载下的动态位移。

上述关于方型电磁轨道发射装置的研究，主要是建立在单层梁的基础上，目前已有双层弹性基础梁动态研究成果，都停留在将电磁炮轨道简化成简支型双层弹性基础梁[15-16]，而其实际结构更接近悬臂式双层弹性基础梁。因此，为完善电磁发射装置理论，找到更加接近实际工况的理论模型是非常必要的。

本文将方型电磁轨道炮的炮管(见图1)简化为悬臂梁，其内部的导轨和壁板简化为悬臂梁内部的上下弹性基础梁，求解了上、下梁在电磁力与电枢力共同载荷作用下的解析和数值解。

图1 方形电磁轨道发射装置简图

1 双层弹性悬臂梁动力学微分方程式的建立

1.1 双层弹性悬臂梁的力学模型及动力学微分方程的建立

发射导轨和外包层壁板简化成Winkler弹性地基上的双层梁体系，双层弹性悬臂梁模型如图2所示。图2中：Eu、Ed分别为上、下梁的弹性模量；Iu、Id分别为上、下梁的惯性矩；EuIu、EdId分别为上、下梁的抗弯刚度；cu、cd分别为上、下梁的弹性常数；l为梁长，le为电枢位置；v为电枢速度。

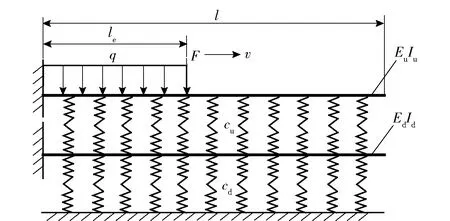
图2 双层悬臂梁力学模型图

上、下梁的动力学平衡方程为

(1)

式中：mu、md分别为上、下梁单位长度的质量，mu=ρuSu,md=ρdSd，ρu、ρd、Su、Sd分别为上、下梁的质量密度与截面面积；wu(x)、wd(x)分别为上、下梁的挠度；t为时间；f(x,t)为集中荷载F(即电枢作用力)和均布荷载q(即作用在轨道上的电磁力)之和，x为集中荷载F的水平位移。

1.2 双层弹性悬臂梁的动力学方程及其通解表达式的建立

根据上、下梁的相互作用关系，在无载荷作用的情况下，上、下梁的动力学方程分别为

(2)

cuwu(x)=0.

(3)

由(2)式可得

(4)

(4)式代入(3)式，化简后有

(5)

根据梁的振动形式，设wu(x)、wd(x)的通解形式分别为

(6)

(7)

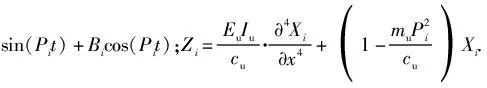
(6)式代入(5)式，可得

(8)

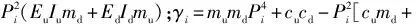
解偏微分方程(8)式，可得

Xi=C1icos(Mix)+C2isin(Mix)+C3icosh(Mix)+

C4isinh(Mix)+C5icos(Nix)+C6isin(Nix)+

C7icosh(Nix)+C8isinh(Nix)，

(9)

(9)式代入(7)式，得到wd(x)表达式中的Zi为

Zi=C1iJicos(Mix)+C2iJisin(Mix)+

C3iJicosh(Mix)+C4iJisinh(Mix)+

C5iKicos(Nix)+C6iKisin(Nix)+

C7iKicosh(Nix)+C8iKisinh(Nix)，

(10)

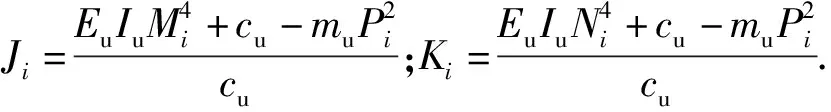
由此可得上、下梁的弯矩分别为

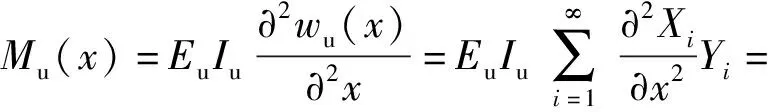
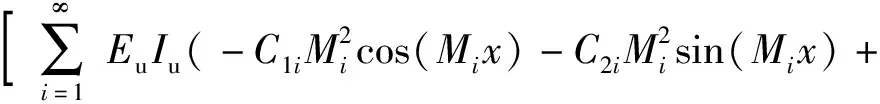
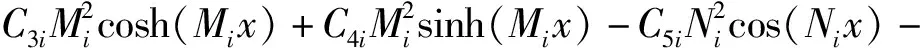
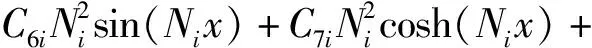
(11)

(12)

上、下梁的转角分别为

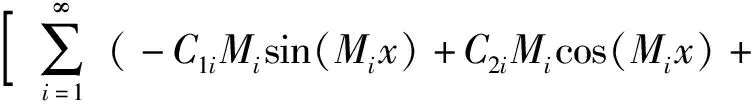
C3iMisinh(Mix)+C4iMicosh(Mix)-C5iNisin(Nix)+

(13)

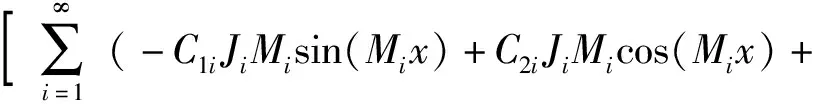
C3iJiMisinh(Mix)+C4iJiMicosh(Mix)-

C5iKiNisin(Nix)+C6iKiNicos(Nix)+

(14)

上、下梁的剪切力

(15)

(16)

系数C1i～C8i由上、下梁的边界条件确定，对照所建立的电磁轨道系统双层梁分析模型，则在上、下梁一端固定约束、一端自由的条件下，所得到的双层梁左、右两端的边界条件为

(17)

(6)式、(7)式、(13)式、(14)式代入(17)式边界条件，可解得

(18)

由此可得到关于上、下梁的模态函数为

Xi=-cos(Mix)+cosh(Mix)-

cos(Nix)+cosh(Nix)-

(19)

Zi=-Jicos(Mix)+Jicosh(Mix)-

Kicos(Nix)+Kicosh(Nix)-

(20)

因此wu(x)和wd(x)可以分别表示为

wu(x)=

sin(Mix))-cos(Nix)+cosh(Nix)-ξi(sinh(Nix)-

sin(Nix))](Aisin(Pit)+Bisin(Pit))，

(21)

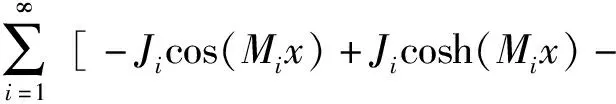
ζiJi(sinh(Mix)-sin(Mix))-

Kicos(Nix)+Kicosh(Nix)-ξiKi(sinh(Nix)-

sin(Nix))](Aisin(Pit)+Bisin(Pit))，

(22)

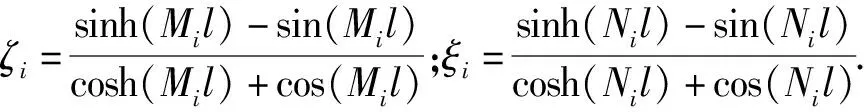
1.3 发射状态下载荷的表达形式

根据双层梁模态函数的正交性，可将多自由度系统模态叠加法的思想应用于连续系统，即将弹性体的振动表示为各阶模态的线性组合，用于计算系统在激励作用下的振动规律，则根据上、下梁的受载状态，其载荷函数为

(23)

式中：δ(·)为Dirac函数；H(·)为Heaviside函数。

由载荷函数(23)式可知，在电枢运动下，双层梁所受载荷可分为两部分，即集中载荷F作用和分布载荷q作用的线性叠加，因此可以将双层梁在载荷下的动力响应表示为这两种载荷下动力响应之和，则双层梁受集中载荷F作用下的载荷函数为

pF(x,t)=-Fδ(x-vt)，

(24)

双层梁受均布载荷q作用下的载荷函数为

pq(x,t)=-qH(vt-x).

(25)

2 集中载荷与均布荷载作用下悬臂式双层梁的动态响应

2.1 集中载荷作用下的上梁动态挠曲线方程

根据(1)式在集中载荷F作用下上梁的动力平衡方程为

pF(x,t).

(26)

(1)式中载荷函数f(x,t)=pF(x,t)=-Fδ(x-vt)，根据上梁受载下动力响应函数的推导，将pF(x,t)代入(21)式，则有

wuF(x,t)=

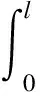
cos(Nix)+cosh(Nix)-ξi(sinh(Nix)-sin(Nix))]·

(27)

根据Dirac函数的性质，将pF(x,t)=-Fδ(x-vt)代入(27)式并积分，可得上梁在集中载荷F作用下的动态响应为

wuF(x,t)=

(28)

2.2 集中载荷作用下的下梁动态挠曲线方程

在集中载荷下上梁的振动响应函数wuF(x,t)确定的条件下，根据(22)式，在受集中力条件下下梁的动力响应为

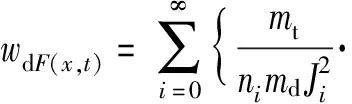
[-Jicos(Mix)+Jicosh(Mix)-ζiJi(sinh(Mix)-sin(Mix))-

Kicos(Nix)+Kicosh(Nix)-ξiKi(sinh(Nix)-sin(Nix))]·

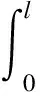
Kicos(Nix)+Kicosh(Nix)-ξiKi(sinh(Nix)-sin(Nix))]·

(29)

2.3 集中载荷作用下的上梁弯矩及应力的动态响应

在已知上梁在集中载荷下动态挠曲线方程的情况下，根据上梁弯矩MuF(x,t)、σuF(x,t)的数值表达式，设hu为上梁截面高度，可由(28)式直接得到

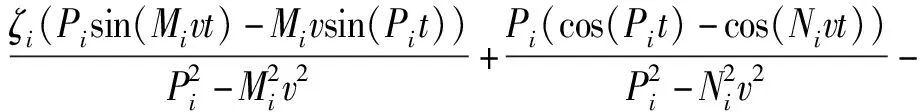
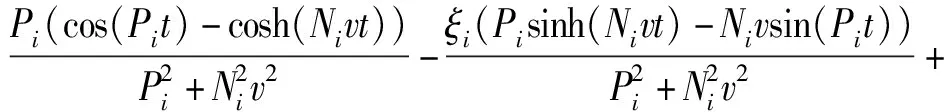
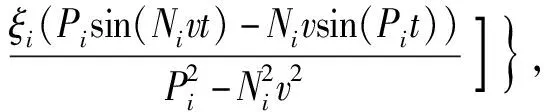
(30)

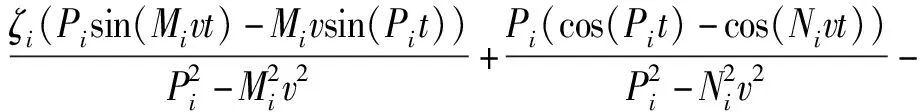
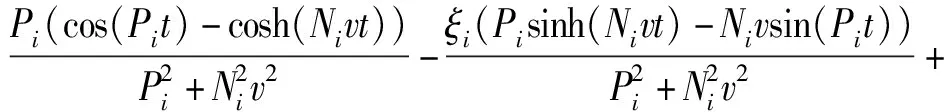
(31)

2.4 集中载荷作用下的下梁弯矩及应力的动态响应

与上梁相类似，已知下梁在集中载荷下动态挠曲线方程的情况下，根据下梁弯矩MdF(x,t)、σdF(x,t)的数值表达式，设hd为下梁截面高度，可由(29)式直接得到

H2)(T1+T2)，

(32)

H2)(T1+T2)，

(33)

c21+c31+c41)，

d21+d31+d41)，

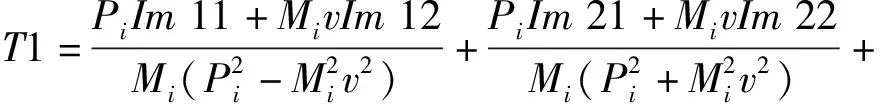
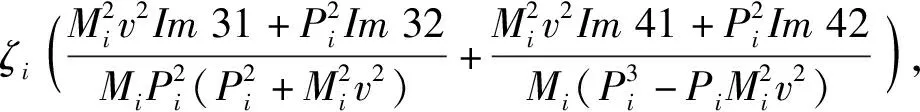
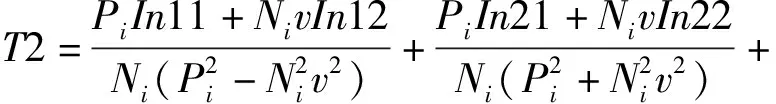
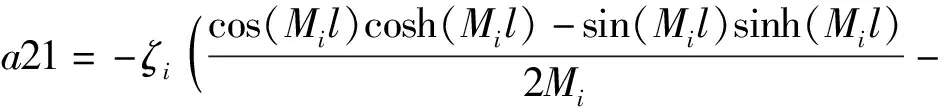
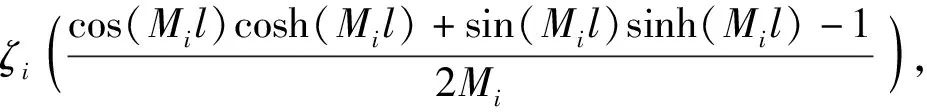
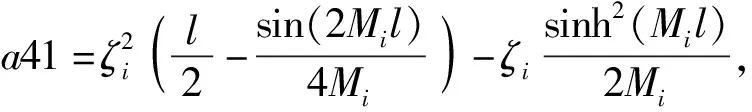
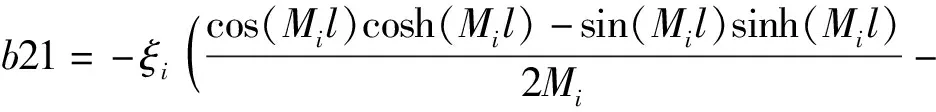
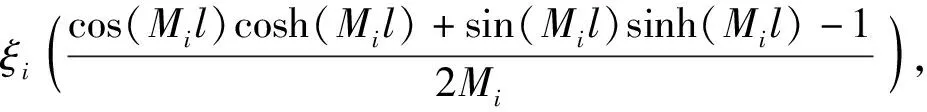
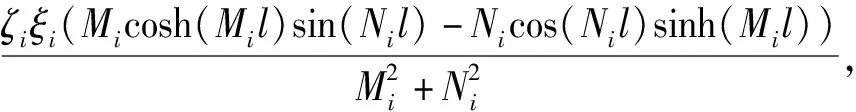
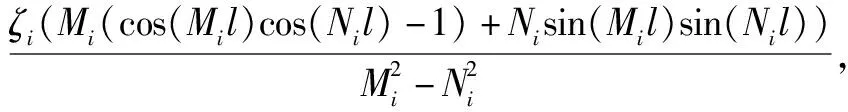
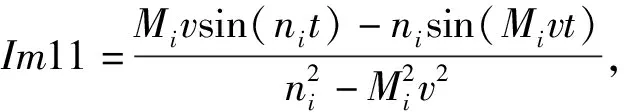
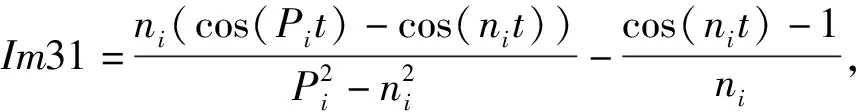
Im41=-Im31，

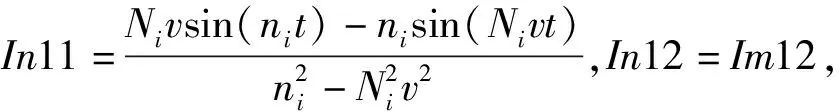
In22=-Im12，In31=Im31，

In32=Im32，In41=-Im31，

3 均布载荷作用下的上、下梁动态挠曲线方程

3.1 均布载荷作用下的上梁动态挠曲线方程

根据(1)式在均布载荷q作用下上梁的动力平衡方程为

wd(x))=pq(x,t)，

(34)

即(1)式中均布函数f(x,t)=pq(x,t)=-qH(vt-x)，pq(x,t)代入(34)式，则有

wuq(x,t)=

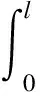
cos(Nix)+cosh(Nix)-ξi(sinh(Nix)-sin(Nix))]·

(35)

根据Heaviside函数的性质，将pq(x,t)=-qH(vt-x)代入(35)式并积分，可得上梁在均布载荷q作用下的动力响应为

(36)

3.2 均布载荷作用下的下梁动态挠曲线方程

均布载荷下的上梁振动响应函数wuq(x,t)确定的条件下，根据对受载条件下的下梁动力响应函数的推导，在受均布载荷条件下，下梁的动力响应为

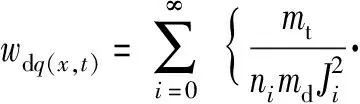
[-Jicos(Mix)+Jicosh(Mix)-ζiJi(sinhMix-sin(Mix))-

Kicos(Nix)+Kicosh(Nix)-ξiKi(sinh(Nix)-sin(Nix))]·

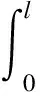
Kicos(Nix)+Kicosh(Nix)-ξiKi(sinh(Nix)-sin(Nix))]·

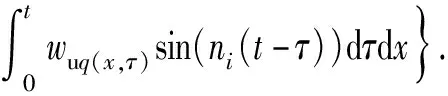
(37)

将推导的上梁在均布载荷下的振动响应函数(36)式代入(37)式并化简，可得到下梁在均布载荷q下的动力响应为

(38)

4 均布载荷作用下的上、下梁弯矩及应力的动态响应

4.1 均布荷载作用下的上梁弯矩及应力的动态响应

在已知上梁在均布载荷下动态挠曲线方程的情况下，根据上梁弯矩Muq(x,t)、σuq(x,t)的数值表达式，可由(36)式直接得到

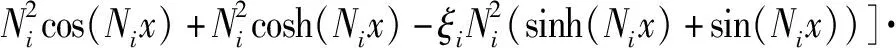
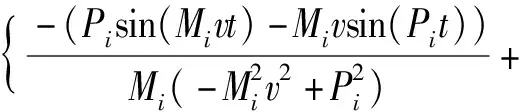
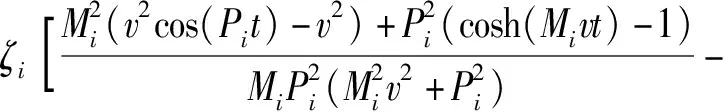
(39)

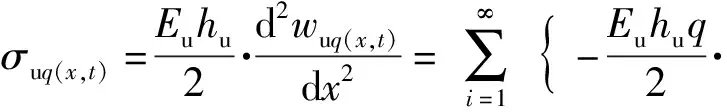
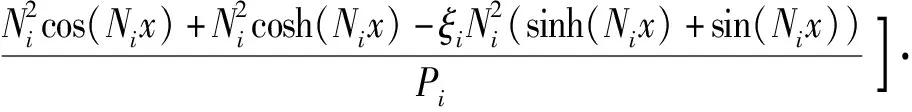
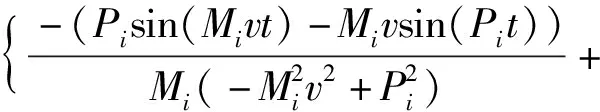
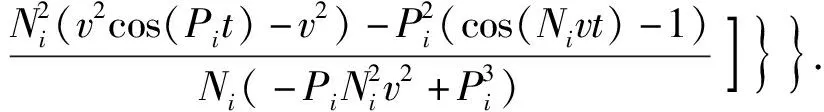
(40)

4.2 均布荷载作用下的下梁弯矩及应力的动态响应

在已知下梁在均布载荷下动态挠曲线方程的情况下，根据下梁弯矩Mdq(x,t)、σdq(x,t)的数值表达式，可由(38)式直接得到

H2)(T1+T2)，

(41)

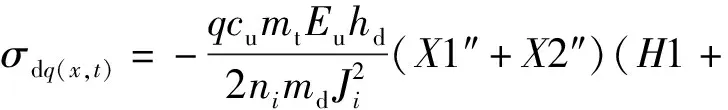
H2)(T1+T2).

(42)

4.3 综合载荷作用下的悬臂式双层梁的弯矩及应力响应

与双层梁的挠曲线方程相类似，对于双层梁的弯矩及应力响应，其也同样具有可加性，则在综合载荷下的上、下梁弯矩及应力的动态响应分别为

Mu(x,t)=MuF(x,t)+Muq(x,t)，

(43)

Md(x,t)=MdF(x,t)+Mdq(x,t)，

(44)

σu(x,t)=σuF(x,t)+σuq(x,t)，

(45)

σd(x,t)=σdF(x,t)+σdq(x,t)，

(46)

式中：MuF(x,t)、MdF(x,t)分别为在集中载荷下的上、下梁弯矩响应；Muq(x,t)、Mdq(x,t)分别为在均布载荷下的上、下梁弯矩响应；σuF(x,t)、σdF(x,t)为在集中载荷下的上、下梁应力响应；σuq(x,t)、σdq(x,t)为在均布载荷下的上、下梁应力响应。

5 综合载荷作用下的悬臂式双层梁动态响应算例分析

5.1 参数的确定

电磁发射导轨的双层梁在综合载荷下的动力学模型如图2所示，截面尺寸如图3所示。其中梁的长度l=3 000 mm，上梁的截面尺寸Hu=45 mm，hu=15 mm，下梁的截面尺寸Hd=75 mm，hd=30 mm.上梁材料为铜，其弹性模量Eu=110 GPa，密度为8 290 kg/m3；下梁材料为尼龙，其弹性模量Ed=28.3 GPa，密度为980 kg/m3;上梁和下梁之间的弹性常数cu=3 MPa，下梁和下层壁板之间的弹性常数cd=6 MPa；上梁承受的均布荷载q=300 N/m，集中荷载F=10 000 N；电枢速度为v=1 000 m/s.

图3 电磁轨道发射装置横断面尺寸图

5.2 计算结果与分析

图4、图5给出了在le=0.5 m综合载荷作用情况下，上梁的弯矩以及应力解析解与有限元分析软件ANSYS数值分析结果的对比。在图4中，弯矩数值解最大值573.6 N·m，解析解最大值601.1 N·m，相对误差为4.8%.在图5中，应力数值解最大值339.6 MPa，解析解最大值356.2 MPa，相对误差为4.9%.图6、图7给出了全程上梁弯矩以及应力随时间和位置的变化。

图4 上梁弯矩分布解析解与数值解的对比

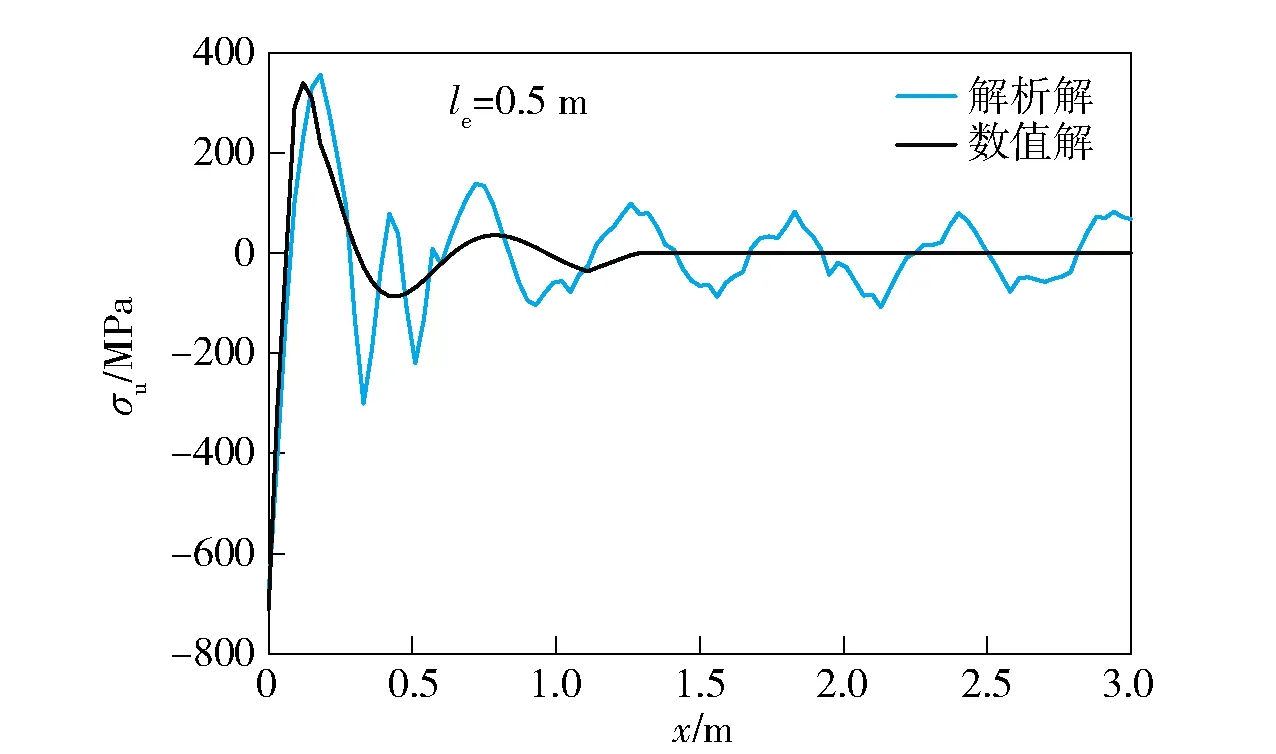
图5 上梁应力分布解析解与数值解的对比

图6 上梁弯矩随时间和位置的变化曲面

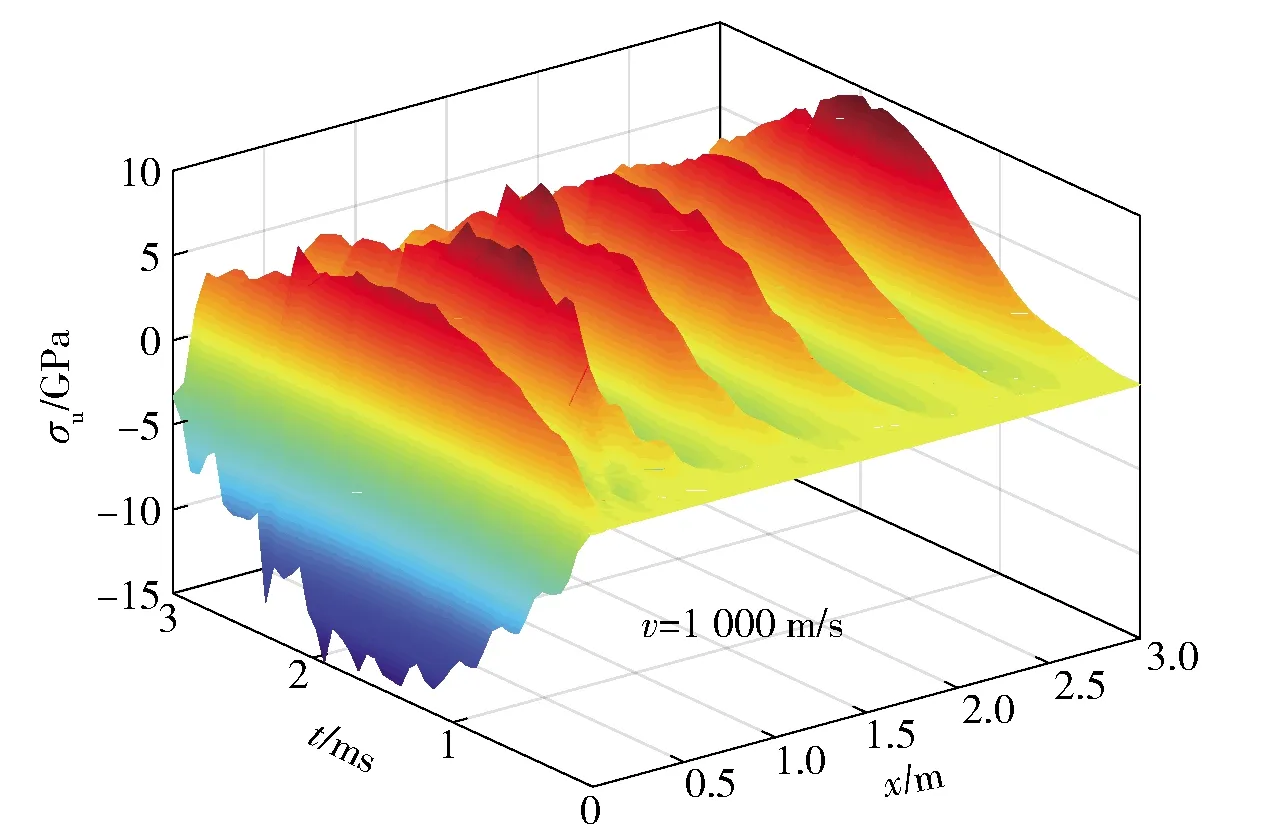
图7 上梁应力随时间和位置的变化曲面

图8 下梁弯矩分布解析解与数值解的对比

图9 下梁应力分布解析解与数值解的对比

图10 下梁弯矩随时间和位置的变化曲面

图8、图9给出了在le=0.5 m综合载荷作用情况下，下梁的弯矩以及应力的数值解与解析解。在图8中，弯矩数值解最大值80.4 N·m，解析解最大值83.6 N·m，相对误差为4.0%.图9给出的应力数值解最大值6.998 MPa，解析解最大值7.262 MPa，相对误差为5.3%.图10、图11给出了全程下梁弯矩以及应力随时间和位置的变化。

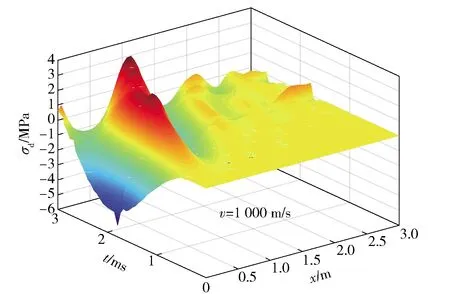
图11 下梁应力随时间和位置的变化曲面

由图4、图5、图8、图9可以看出，数值解与解析解的最大值比较接近，且都发生在0～0.5 m范围之内，而后解析解出现了波动，是由于在双层弹性梁模型的解析解求解时未考虑层间阻尼造成的。同时，对比上、下梁的动态响应值，上梁的响应值明显高于下梁的，表明电磁轨道比外层壁板受移动荷载影响要大。通过图4、图5、图8和图9中两种解法结果的对比，不难发现解析解与数值解吻合得比较好。

6 结论

本文建立了方型电磁发射装置的双层弹性基础悬臂梁模型，分别采用Heaviside函数和Dirac函数建立导轨及壁板的动力学微分方程，用解析法求解其在工作状态下的动态响应，并使用数值法求解与之进行比较。得到以下结论：

1)双层弹性悬臂梁动态响应的解析解与数值解存在一定的差异，但结果总体较为吻合，解析解的可靠性在一定程度上通过其与数值解的对比得到了验证。

2)对于双层悬臂梁模型的电磁炮，轨道动态响应比外壁板的响应大，而且峰值基本位于0～0.5 m之内，在进行电磁炮设计时，应注意轨道及其固定端的加强。

3)本文建立的双层弹性悬臂梁模型及导出的动态响应的解析解，能够帮助完善电磁轨道发射装置的理论研究，并可供相关领域的工程设计计算参考。