一类线性化多项式的核

金 永, 姜敬敬

(中国民航大学 理学院, 天津 300300)

1 引言与预备知识

设p为素数,m为正整数,Fpm表示含有pm个元素的有限域.具有下列形式的多项式称为Fpm到Fp的迹函数[1]:

Tr(x)=x+xp+xp2+…+xpm-1.

这里的迹函数实质上是文献[1]中的绝对迹函数.若将上述素数p换成素数幂, 即为一般意义下的迹函数.一般地, 具有如下形式的多项式:

称为Fpm上的线性化多项式.

有限域上迹函数的概念具有重要意义, 可直接用于定义线性码[2-3].此外, 有限域上的指数和在编码理论中应用广泛[4-8].

本文考虑的迹函数均指绝对迹函数, 如果已知有限域的子集与迹函数的核的交集中元素的个数, 则将对刻画对应线性码的参数以及简化指数和的计算有益[1].本文考虑下列问题: 对于给定的非负整数s(≤m), 给出一些线性化多项式L, 使其满足dim(ker(L)∩ker(Tr))=s.本文考虑最基本的情形:s=0, 即

ker(L)∩ker(Tr)={0}.

文献[9]基于迹函数给出了线性化多项式核的维数描述.本文从另一角度, 不借助迹函数, 给出满足要求的线性化多项式.设

L(x)=xpk+ak-1xpk-1+…+a1xp+a0x(k≤m-1),N=ker(L),L0(x)=xp-x.

定义LN如下:

LN(x)=L∘L0(x)=xpk+1+(ak-1-1)xpk+(ak-2-ak-1)xpk-1+…+(a0-a1)xp-a0x.

因此LN也是线性化多项式且LN(1)=0.下面记

LN(x)=xpk+1+bkxpk+…+b1xp+b0x,

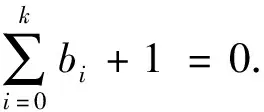
设l(x)=xk+1+bkxk+…+b1x+b0为LN的相伴多项式[1].设C为l(x)的友矩阵, 以下也称C为LN的友矩阵.设σ为Fpm的Frobenius自同构, 即σ(a)=ap,a∈Fpm.Cσi表示将C的每个元素用自同构xpi作用后得到的矩阵.令A为

A=CCσCσ2…Cσm-1,

利用文献[10]中定理5将本文的问题进一步转化为考虑矩阵A-I的秩.

设b0≠0,LN(x)∈Fp[x], 则C可逆且A=Cm.此时, 为了考虑ker(LN)只需考虑rank(Cm-I).但此时的C为线性递归序列的状态转移矩阵, 完全刻画rank(Cm-I)很困难[1].本文考虑ord(C)|(m-2)的情形, 通过分析矩阵C+I的秩, 给出其可逆的充要条件, 基于此给出一类满足ker(L)∩ker(Tr)=0的线性化多项式L, 并给出L的计算方法.

2 主要结果

设

LN(x)=xpk+1+bkxpk+…+b1xp+b0x∈Fp[x],LN(1)=0.

记l(x)=xk+1+bkxk+bk-1xk-1+…+b1x+b0为LN(x)的相伴多项式[1].设C为LN的友矩阵.易知l(x)是C的特征多项式, 即l(x)=det(xI-C), 其中I表示k+1阶单位矩阵.若f(x)为多项式, 则用ord(f(x))表示其阶, 即满足f(x)|(xd-1)的最小正整数.

引理1[1]设b0≠0, 则ord(l(x))=ord(C), 其中ord(C)指C在一般线性群GLk+1(Fp)中的阶.

由定义知线性化多项式LN、 矩阵C以及l(x)之间相互决定.一般地,xm-1的分解依赖于具体的p和m.定义p关于m的阶为满足pt≡1(modm)的最小正整数t.记xm-1在Fpt中的全体根为E(m).

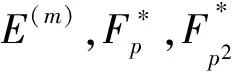
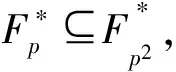
由ord的定义可得下列两个引理:

引理4设f(x)为m-2次首一多项式,m≥5, 则ord(f(x))=m当且仅当f(x)|(xm-1).

引理5设b0≠0且ord(C)=r.若r|(m-s), 则rank(Cm-I)=rank(Cs-I).

引理6rank(C-I)=k.

证明: 因C-I有一个k阶非零子式, 故rank(C-I)≥k.又因l(1)=LN(1)=0, 故det(C-I)=0.于是rank(C-I)=k.

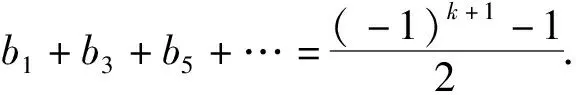
证明: 注意到C+I有一个k阶的非零子式, 故rank(C+I)≥k.再注意到l(1)=LN(1)=0.当p=2时, 总有det(C+I)=0, 故rank(C+I)=k.当p≠2时, rank(C+I)=k当且仅当det(C+I)=0, 当且仅当l(-1)=0.因l(1)=0, 故l(-1)=0等价于l(1)-l(-1)=0, 即

2(b1+b3+b5+…)+(1-(-1)k+1)=0.

(1)

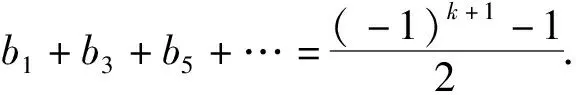
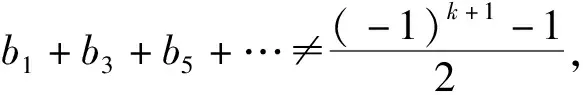
证明：只需注意到C2-I=(C+I)(C-I), 再利用引理6和引理7可得结论.

引理8dim(ker(L)∩ker(Tr))=dim(ker(LN))-1.

证明: 由于LN(x)=L∘L0(x),L0的像集恰好为迹函数Tr的核，所以易知ker(LN)中元素个数与ker(L)∩ker(Tr)中元素个数为p个对应1个，进而可得所证结论.

引理9[9]ker(LN)=k+1-rank(A-I).

定理1设L(x)=xpk+ak-1xpk-1+…+a1xp+a0x是Fpm上的线性化多项式,N=ker(L).假设LN(x)=xpk+1+bkxpk+…+b1xp+b0x∈Fp[x].若b0≠0,p≠2, ord(C)|(m-2), 则dim(ker(LN))≤2.进一步, dim(N∩ker(Tr))≤1.特别地, 当C+I可逆时, dim(ker(LN))=1, 此时有N∩ker(Tr)={0}.

证明：由引理9知

dim(ker(LN))=k+1-rank(Cm-I).

当b0≠0且ord(C)|(m-2)时,Cm-I=C2-I=(C+I)(C-I).由引理6和引理7知, rank(C+I)≥k, rank(C-I)=k.故

rank(Cm-I)=rank((C+I)(C-I))≥rank(C+I)+rank(C-I)-(k+1)≥k-1.

所以dim(ker(LN))≤(k+1)-(k-1)=2.而当C+I可逆时, 显然有

rank(C2-I)=rank((C+I)(C-I))=rank(C-I).

从而有dim(ker(LN))=1.进而由引理8可得N∩ker(Tr)={0}.

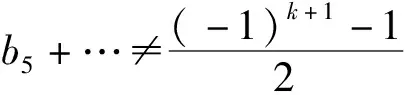
证明：由引理8及定理1可得结论.

步骤1)计算s=gcd(p-1,m),s′=gcd(p2-1,m);

步骤2)求出xm-2-1的一个不能被x-1整除的、 首一的二次因子h(x);

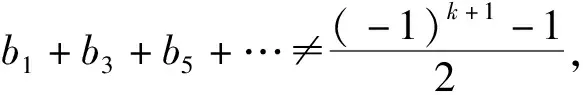
例1设p=5,m=18,xm-2-1=x16-1.则5关于16的阶为4,

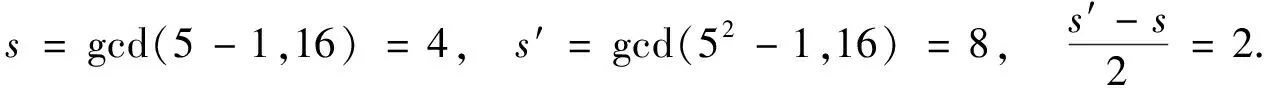
求x16-1在F5[x]中的因子(x-2)(x-4).计算

此时

b1+b3+b5+…+b13=4≠0,

故其相伴线性化多项式

L(x)=xp13+2xp12+xp9+2xp8+xp5+2xp4+xp+2x

满足ker(L)∩ker(Tr)={0}.