电磁发射磁探针阵列位置分布及姿态优化

王振春， 张玉婷， 鲍志勇， 刘福才， 战再吉

(1.燕山大学 工业计算机控制工程河北省重点实验室， 河北 秦皇岛 066004；2.燕山大学 亚稳材料制备技术与科学国家重点实验室， 河北 秦皇岛 066004)

0 引言

电磁发射技术具有动能大、速度可控及安全性高等优点，已成为新概念武器研究的热点[1-3]。在发射过程中，电枢速度和位移等参数的测量可以从一定程度上反映电枢在内弹道中的运动状态，准确测量内弹道中的电枢速度对电磁发射具有重要意义[4-5]。磁探针具有价格低、体积小、耐震耐热性好等优点，是电磁发射中最常用的电枢速度测量传感器。其原理为检测电枢经过磁探针时引起的磁通变化，得到电枢通过磁探针的时间[6]，拟合求导后得到电枢速度- 时间曲线[7]。

影响电枢速度曲线拟合精度的主要原因包括磁探针阵列(即多个测量电枢速度的磁探针)的空间位置分布、电枢速度曲线测量方法的选取等[8]。刘福才等[9]提出采用探针串联和波形叠加两种新方法进行增强型电磁轨道炮膛内电枢速度测量。Cao等[10]提出用结合法来提高电枢拟合速度、位移曲线的精度。电枢在启动阶段加速度大、速度变化快，应有更多的磁探针来测量启动阶段的电枢速度。而电枢后期加速度小、速度变化慢，磁探针数量相对于启动阶段可减少。由此可见，磁探针阵列的安装位置会对电枢曲线拟合精度造成影响，但目前关于如何确定磁探针阵列的安装位置，使得电枢速度曲线拟合精度更高的研究较少。

影响磁探针电枢速度测量精度的主要因素包括磁探针在膛内的安装方式、安装深度、安装高度和磁探针特征点(电枢通过磁探针的时间)的选取等[11]。王咸斌等[12]对选取探针过零点时刻引起的误差进行分析，得出在电流导数不为0时，B探针过零点时刻并不是电枢通过探针的时刻。李菊香等[13]对探针安装偏差引起的测速误差进行了详细研究，发现B探针的安装位置偏差及角度偏差越大，测速误差越大，并提出用二次多项式拟合方法来减小探针速度测量误差。由于磁探针理论研究忽略了较多的影响因素以及实际试验中探针数据的不足等因素，关于磁探针在内弹道中的安装方式选取、安装深度以及安装高度对测速误差影响的研究较少，均未研究磁探针在何种姿态下测量精度更高。

本文针对电枢速度曲线拟合精度以及磁探针测量精度两个问题，采用道格拉斯- 普克(Douglas-Peucker)数据处理方法确定磁探针阵列位置分布问题，发现磁探针阵列的位置分布具有前密后疏的排列特点。建立磁探针感应电压的数学公式模型，得到磁探针在膛内的安装方式、安装深度、安装高度和探针感应电压之间的关系，进一步得到测量精度更高的磁探针空间姿态。最终得到磁探针测量电枢出口速度的理论相对误差在2‰以内，内弹道电枢速度曲线的理论相对误差可控制在5‰以内。

1 磁探针阵列位置分布及测速原理

1.1 基于Douglas-Peucker算法的数据处理方法

Douglas-Peucker 算法[14]是将曲线近似表示为一系列点，并在保持曲线精度前提下减少点的个数的一种算法。该算法通过设置一个阈值作为最大误差范围，来选取一系列点，使得这些点的误差在允许误差范围内，其优点是给定曲线与阈值后抽样结果一定。图1所示为Douglas-Peucker 算法原理图。图1中，A、B为线段端点，C、D、E分别为距离线段AE、EB、AB距离最远的点。

图1 Douglas-Peucker算法原理图Fig.1 Schematic diagram of Douglas-Peucker algorithm

在电磁发射实验中，通过对电枢时间- 位移曲线进行数据压缩，即在保证原有位移曲线精确度的情况下，删除曲线中部分位移- 时间点，可实现速度测量点个数的良好压缩。在位移- 时间曲线中，数据压缩步骤如下：

步骤1将位移曲线首尾虚连成一条线段，如图1(a)中线段AB，假设该直线表示为y=kx+p，x为直线AB中任意点横坐标，y为对应纵坐标，k为直线斜率，p为截距。根据(1)式判断出所有点与直线的距离，并找出最大的距离值D，

(1)

步骤2比较最大距离D与预先给定的阈值的大小，如果小于阈值，则以该直线作为曲线的近似，该段曲线处理完毕。

步骤3如果最大距离D大于阈值，则距离最大的点将曲线分为两段，如图1(b)中线段AE和线段EB，并分别对每段曲线进行步骤1～步骤3的处理。

步骤4当所有曲线都处理完毕后，依次连接各个分割点形成折线，作为位移曲线的近似。

1.2 磁探针原理

磁探针是电磁发射系统常用的速度传感器。通常采用多个磁探针(磁探针阵列)来测量电枢在内弹道中的速度，磁探针阵列安装实物图如图2(a)所示，安装示意图如图2(b)所示，其中c为磁探针间距。磁探针根据安装方式可分为电枢磁探针和轨道磁探针两种。电枢磁探针线圈的法线方向平行于轨道电流方向，其特点为线圈主要感应电枢电流产生的磁场；轨道磁探针线圈法线方向平行于电枢电流方向，其特点为线圈主要感应轨道电流产生的磁场。

图2 磁探针阵列图Fig.2 Magnetic probe array

增强型发射器磁探针示意图如图3所示。图3中：a为两导轨距离的一半；a1为探针中心距上轨道平面距离；a2为探针中心距下轨道平面距离；b为磁探针安装深度，即探针中心距两轨道中轴所构成竖直平面距离；l为电枢起始位置距磁探针的水平距离；s(t)为电枢的运动位移，s(t)关于时间求导得到电枢的运动速度v(t)；d为内外轨道之间的距离；N为线圈匝数；A为单匝线圈的面积。

图3 增强型发射器磁探针示意图Fig.3 Schematic diagram of enhanced transmitter magnetic probe

磁探针安装方式为电枢磁探针时，磁探针线圈感应电枢电流、电枢运动及内外轨道连接导体中电流产生的磁场。在发射过程中任一时刻t,由毕奥- 萨伐尔定律可知电枢磁探针感应的磁通量Φa(t)为

(2)

式中：μ0为真空磁导率，μ0=4π×10-7T·m/A；I(t)为电枢电流。

因此，电枢磁探针中产生的感应电动势ea(t)为

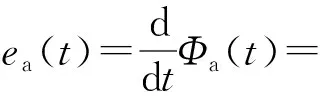
(3)

式中：I′(t)为电枢电流导数。

同理，由左、右两侧连接体产生的感应电动势eL(t)及eR(t)为

(4)

式中：w为轨道长度。

综上所述，电枢磁探针总感应电动势eatot(t)为

eatot(t)=ea(t)-eL(t)-eR(t).

(5)

由(5)式可以看出，电枢磁探针中电枢引起的感应电动势由两部分组成，一部分与电流变化引起的感生电动势有关，一部分与导体运动引起的动生电动势有关；而内外轨道连接体引起的感应电动势仅与电流变化引起的感生电动势有关。

同理，对于轨道磁探针，磁探针线圈感应内外轨道中电流变化及电枢运动产生的磁场，由内轨道电流变化及电枢运动产生的感应电动势eir(t)为

(6)

轨道磁探针中外轨道产生的感应电动势eor(t)为(7)式：

(7)

式中：Φor(t)为外轨道电流通过磁探针线圈平面的磁通量。

轨道磁探针总感应电动势er(t)为

er(t)=eir(t)+eor(t).

(8)

由(8)式可以看出：轨道磁探针中内轨道引起的感应电动势由两部分组成，一部分与轨道电流变化引起的感生电动势有关，一部分与电枢运动引起的动生电动势有关；外轨道引起的感应电动势仅与外轨道电流变化引起的感生电动势有关。

2 磁探针阵列研究

2.1 磁探针阵列空间分布研究

采用表1所示参数进行仿真，电枢的位移- 时间曲线如图4所示，电枢出口速度为793 m/s.

表1 仿真实验参数

图4 电枢位移- 时间曲线Fig.4 Armature displacement-time curve

为得到发射器上的速度测量点分布位置，距离阈值设为0.01 mm，对图4中的位移- 时间曲线采用Douglas-Peucker算法进行数据压缩，得到14个速度测量点，如图5所示。

图5 Douglas-Peucker算法处理结果Fig.5 Processing results of Douglas-Peucker algorithm

对磁探针阵列感应电压进行仿真，磁探针放置方式为电枢磁探针，入膛深度为0.017 5 m，磁探针安装高度为上下轨道中心位置处，仿真结果如图6所示。

图6 磁探针感应电压Fig.6 Induced voltage of magnetic probe

相同实验条件下，采用等间隔放置磁探针的方式，从距离轨道尾部0.11 m位置处开始，每隔0.13 m放置1个探针，共15个磁探针。用于与采用Douglas-Peucker算法确定的磁探针分布位置进行对比，等间隔放置磁探针时感应电压如图7所示。

图7 等间隔磁探针感应电压Fig.7 Induced voltage of equidistant magnetic probe

选择磁探针感应电压过零点对应的时间作为电枢通过磁探针的时间，使用三次样条插值法进行拟合[15]，得到电枢位移- 时间曲线如图8所示，求导后得到速度- 时间曲线如图9所示。

图8 电枢位移- 时间曲线Fig.8 Displacement-time curves of armature

图9 电枢速度- 时间曲线Fig.9 Speed-time curves of armature

图9中黄色曲线为等距离安装磁探针阵列所得电枢速度曲线，Douglas-Peucker算法确定的磁探针阵列所得电枢速度曲线为红色曲线。由图9可以看出：采用Douglas-Peucker算法确定的磁探针阵列所得电枢速度曲线能更好地逼近电枢速度曲线；经曲线拟合后的电枢出口速度为796.5 m/s，电枢曲线的出口速度理论相对误差为4.7‰. 电枢曲线的出口速度理论相对误差定义如(9)式所示：

(9)

式中：vln为电枢速度曲线拟合的电枢出口速度；vs为电磁发射系统仿真模型得到的理论电枢出口速度；ele为电枢速度曲线的出口速度理论相对误差。改变仿真实验条件，使得充电电压从1 500 V开始，每次增加300 V，直到3 000 V，得到出口速度相对误差如表2所示。由表2可以看出，电枢曲线的出口速度理论相对误差能控制在5‰以内。

表2 不同充电电压下出口速度误差

2.2 磁探针阵列空间姿态研究

实际试验中，通常选择电枢磁探针感应电压过零点的时间或轨道磁探针感应电压峰值的时间，作为电枢通过磁探针的时间。理论上，t0时刻电枢通过电枢磁探针(s(t0)=l)时，代入(5)式得到电枢磁探针感应电压差值Δeatot如(10)式所示。同理，在tf时刻电枢通过轨道磁探针时(s(tf)=l)，代入(8)式得到轨道磁探针感应电压差值Δer为(11)式所示。

(10)

(11)

采用表1所示仿真条件，由(10)式和(11)式结合仿真软件，得到轨道发射过程中，任意位置处电枢磁探针和轨道磁探针的感应电压差值分别如图10中红色和黑色曲线所示。

图10 磁探针感应电压误差Fig.10 Induced voltage errors of magnetic probe

由图10可知：在电流上升阶段，电枢磁探针和轨道磁探针感应电压差值大于0 V；在电流下降阶段，电枢磁探针和轨道磁探针感应电压差值小于0 V；电流斜率越大，磁探针测量误差越大，在电流斜率为0 kA/m时，磁探针感应电压差值为0 V.

在电流上升和下降阶段分别对比两种磁探针的位置测量偏差，结果如图11所示。磁探针测量位置偏差es如(12)式所示：

es=|s′-s|，

(12)

式中：s′为电枢磁探针感应电压为0 V(轨道磁探针感应电压峰值)时对应的磁探针位置；s为电枢磁探针(轨道磁探针)的真实仿真位置。

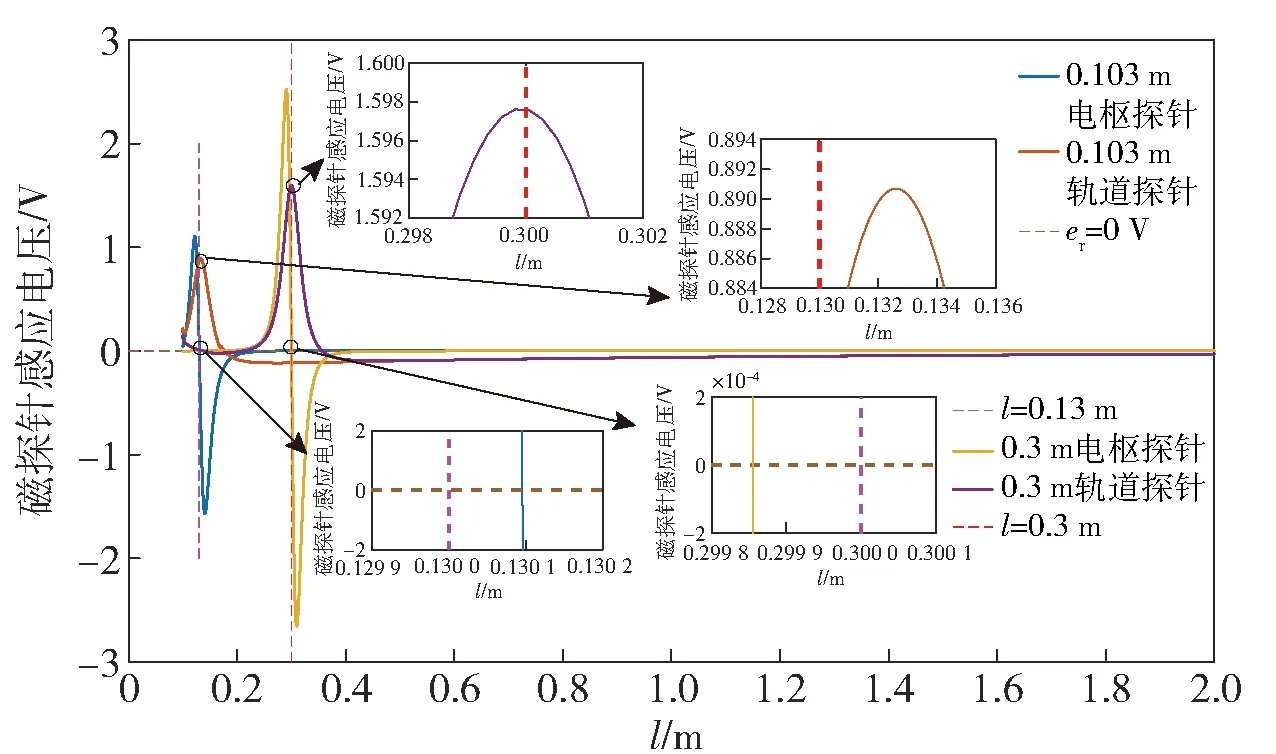
图11 两种磁探针感应电压图Fig.11 Induced voltages of two kinds of magnetic probes

由图11可见，磁探针安装位置在0.13 m处，电流处于上升阶段，电枢磁探针感应电压过零点对应位置为0.130 095 m，电枢磁探针测量位置偏差为0.000 095 m，轨道磁探针感应电压最大值对应位置为0.132 m，轨道磁探针测量位置偏差0.002 m. 在0.3 m位置处，电流处于下降阶段，电枢磁探针测量位置偏差为0.000 15 m，轨道磁探针测量位置偏差为0.000 2 m. 由此可以看出，电枢磁探针测量位置偏差要小于轨道磁探针测量位置偏差，因此选择电枢磁探针安装方式。

磁探针安装方式和安装深度不变，安装高度由距离上轨道平面0 m开始，每次增加0.003 5 m，直到0.035 m，发射过程中0.3 m位置处电枢磁探针感应电压如图12所示，轨道磁探针感应电压如图13所示。

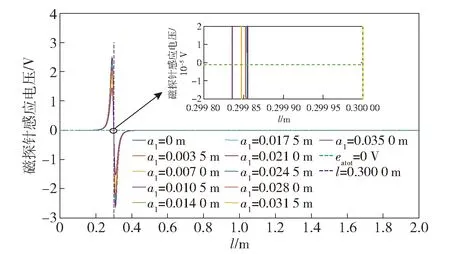
图12 不同安装高度的电枢磁探针感应电压Fig.12 Induced voltages of armature magnetic probe at different installation heights

图13 不同安装高度的轨道磁探针感应电压Fig.13 Induced voltages of track magnetic probe at different installation heights

由图12可以看出，电枢磁探针安装高度越接近上下轨道中点位置，电枢磁探针测量位置偏差越小。由图13可以看出，与电枢磁探针相似，轨道磁探针安装高度越接近上下轨道中点位置，轨道磁探针测量位置偏差越小。

保持磁探针安装方式及安装位置不变，安装深度从距离上下轨道中轴构成的竖直平面距离为0.012 m开始，每次增加0.006 m，直到0.03 m，其电枢磁探针感应电压如图14所示，轨道磁探针感应电压如图15所示。

图14 不同安装深度的电枢磁探针感应电压Fig.14 Induced voltages of armature magnetic probe at different installation depths

图15 不同安装深度的轨道磁探针感应电压Fig.15 Induced voltages of track magnetic probe at different installation depths

由图14中可知，电枢磁探针距离轨道中轴竖直平面距离越小，电枢磁探针测量位置偏差越小。图15所示为不同安装深度的轨道磁探针感应电压。对于图15中的轨道磁探针，仍然有如下结论成立：磁探针距离轨道中轴竖直平面距离越小，轨道磁探针测量位置偏差越小。但由于实际发射试验中电枢具有一定的宽度，磁探针与轨道竖直平面中轴的距离不可能为0 m，为避免磁探针与电枢碰撞，磁探针安装距轨道竖直平面中轴的距离应大于电枢宽度的一半。

综上所述，磁探针的安装姿态会影响磁探针测量精度：磁探针采用电枢磁探针的安装方式，安装位置选择上下轨道中点位置，安装深度越深，磁探针测量误差越小；当磁探针安装深度为电枢宽度的一半时，电枢出口速度为792.27 m/s，磁探针测电枢出口速度的理论相对误差为1.6‰. 电枢出口速度的理论相对误差ee计算如(13)式所示。改变仿真条件中的充电电压，得到不同的电枢出口速度，可知磁探针测量的理论相对误差可以控制在2‰以内。

(13)

式中：vd为磁探针阵列仿真得到的电枢出口速度。

3 试验测试与分析

在10个充电电压为1 500 V的脉冲电源模块等间隔10 μs放电情况下，重复进行8次发射试验。轨道一侧采用Douglas-Peucker算法确定的变间隔安装方式，分别放置在0.11 m、0.13 m、0.15 m、0.21 m、0.26 m、0.37 m、0.48 m、0.60 m、0.75 m、0.85 m、1.20 m、1.42 m、1.90 m、1.95 m位置处，另一侧在0.20 m、0.50 m、0.80 m、1.10 m、1.50 m、1.90 m位置处放置6组共18个磁探针，每组内3个磁探针等间隔为0.05 m放置。

受实际发射条件影响，本文仅对电枢安装深度带来的影响进行验证。在变间隔放置侧，采用优化后的安装深度，均为电枢宽度的一半(0.017 5 m)；在等间隔放置侧，除炮口位置处两个探针采用未优化的安装深度(0.016 m)外，其余探针安装深度为0.017 5 m. 以第7次试验为例，变间隔放置侧，磁探针波形如图16所示；等间隔放置侧，磁探针波形如图17所示。

图16 变间隔磁探针电压波形Fig.16 Voltage waveform of variable interval magnetic probe

图17 等间隔磁探针电压波形Fig.17 Voltage waveform of equispaced magnetic probe

考虑到试验中的随机干扰因素，使用高阶过零法，滤除磁探针感应电压中的高频杂波，得到磁探针感应电压过零点时间。对每次发射试验的电枢速度曲线求平均值，得到电枢平均速度曲线如图18所示。通过与图9中理论电枢速度曲线对比可知，磁探针采用变间隔放置方式，在电枢发射过程中可以更好地拟合电枢速度曲线。

图18 电枢平均速度曲线对比图 Fig.18 Comparison of armature average speed curves

针对8次发射试验，优化后的磁探针安装深度所测电枢初速vo、未优化的磁探针安装深度所测电枢初速vno及激光靶[16]所测电枢初速vla如表3所示。对于每次试验，由(14)式得到每次试验优化后磁探针安装深度所测电枢初速的相对误差为eo，未优化磁探针安装深度所测电枢初速的相对误差为eno. 对8次试验所得相对误差求平均值得到平均相对误差，优化后磁探针测量平均相对误差为2.25%，未优化磁探针平均相对误差为2.96%. 故优化后磁探针安装姿态的测量精度更高，电枢出口速度为700～800 m/s时，优化后磁探针测量平均相对误差为2.25%.

表3 电枢出口速度对比

(14)

4 结论

本文将Douglas-Peucker算法应用于磁探针阵列位置分布及精度研究，研究了磁探针阵列三维安装姿态对磁探针测量精度的影响。得出主要结论如下：

1)将Douglas-Peucker算法应用在电磁发射领域，实现电枢速度曲线的精确拟合，电枢速度曲线的出口速度理论相对误差在5‰以内。

2)得出了磁探针感应电压与安装方式、高度及深度等相关物理量之间的关系，并优化磁探针阵列安装姿态，使磁探针测量精度更高。磁探针测量电枢出口速度的理论相对误差在2‰以内。

3)通过实际试验进行了分析，验证了文中所提磁探针阵列安装位置及安装姿态具有更高的测量精度。