轻型无后坐力炮的动不平衡冲量特性

庞春桥， 陶钢， 李召， 闻鹏， 任保祥， 李智宇

(1.南京理工大学 能源与动力工程学院， 江苏 南京 210094； 2.63961部队， 北京 100012)

0 引言

无后坐力炮是指一种通过尾部喷管将发射药燃烧生成物喷射出去，以抵消弹丸发射后坐力的武器。后坐力小、质量轻是此类武器的主要优点，也是设计人员追求的目标。目前，无后坐力炮的相关文献多为研究所或公司的研究报告[1]。针对无后坐力炮动不平衡冲量的研究，大部分集中在弹丸出膛以前的内弹道过程，而弹丸出膛后剩余火药燃气对动不平衡冲量的影响研究几乎没有受到关注，原因在于传统的平衡力测试技术受到限制，难以深入探索其物理过程。

关于发射平衡力的问题，文献[2]给出了75 mm无后坐力炮发射不平衡力与喷管结构的关系。文献[3]通过建立准两相流内弹道模型，计算了无后坐力炮动不平衡力随内弹道时间的变化规律。文献[4]介绍了后效期对无后坐力炮动不平衡冲量的影响，给出了理想无后坐条件，但是这种理想条件在实际中是不存在的。文献[5]研究了带状变燃速发射药对无后坐力炮内弹道的影响，并给出了其对动不平衡冲量的影响。文献[6]研究了炮尾封闭式武器后效期对身管后坐的影响。文献[7]为了研究枪械后坐力对运动员的影响，设计了一种能够模拟运动员射击状态的后坐力测试系统。文献[8]对影响单兵武器发射器动不平衡冲量的因素进行了分析。文献[9-10]针对大口径武器提出了双药室喷管气流反推减后坐技术，并进行了试验验证。文献[11]设计了一种时延式喷管气流反推减后坐装置，并进行了仿真计算。文献[12]利用拉压力传感器设计了一种动不平衡力的测量装置，对78式82 mm无后坐力炮的动不平衡冲量进行了研究，但是对于测试结果中的波动并未给出具体原因。

本文利用自行设计的精密平衡测试装置，精确测量了不同喷管状态、装药、温度等条件下发射器动不平衡位移随时间的变化过程，发现在弹丸出膛后仍存在两个时期(后效期和后后效期)的影响过程，而且不可忽略。通过将后后效期气动作用过程的试验结果和振动系统运动稳定性理论相结合，提出了一种轻型无后坐力炮动不平衡冲量现象的物理解释和有效评估方法。该方法不仅可以得到轻型无后坐力炮发射时的动不平衡冲量，还可以得到弹丸出膛以后剩余火药燃气对发射器的作用规律。本文所得成果可以为轻型无后坐力炮及其同类型武器动不平衡冲量的研究提供参考。

1 动不平衡试验

动不平衡冲量是无后坐力炮非常重要的参数，直接关系到该武器的性能，因此需要通过试验来考察设计参数的合理性。传统的动不平衡参数测试方法是弹道摆测试[13-14]，但是由于轻型无后坐力炮质量较轻，弹道摆测试需要配重，摆杆长度需要大幅度加长才能满足测试要求，操作极为不便。此外，该方法在操作过程中误差较大，且只能得到最终效果，不便于对动不平衡冲量的精确研究。因此，迫切需要一种新的测试方法取代弹道摆试验，即通过数据采集设备和传感器记录无后坐力炮发射时的运动状态，从而间接得到其动不平衡冲量，这种新方法还可以为动不平衡冲量的精确研究提供数据支撑。

1.1 测试系统布置

为了有效评估轻型无后坐力炮动不平衡冲量及弹丸出膛后剩余火药燃气对发射器的气动作用规律，测试系统布置如图1所示。发射器水平安装在炮架滑块之上，位移传感器一端与炮架底座相连，另一端与炮架滑块相连。在发射过程中，滑块与发射器一同在轨道上滑动，用数据采集仪记录发射器的位移时间数据，通过数据处理得到测试系统中滑动部分的最大速度，与滑动部分的质量相乘即可得到被测试轻型无后坐力炮的动不平衡冲量。测试系统中的传感器为上海极典公司生产的拉杆式位移传感器，数据采集设备为奥地利Dewesoft公司生产的SIRIUS系列数据采集系统，采样频率为20 kHz. 日本Fastcam公司产Mini UX50高速相机布置在发射器侧面，拍摄速率为10 000帧/s，监测发射过程及弹丸出膛后膛内剩余火药燃气的前后喷射情况。

图1 动不平衡冲量测试系统示意图Fig.1 Schematic diagram of dynamic imbalance impulse test system

1.2 测试系统标定

为了验证测试系统的精度，通过动量守恒原理对测试系统进行标定。首先将图1中发射器换成枪弹回收桶，利用56式冲锋枪对回收桶内进行射击，回收桶内的填充物可以有效地回收枪弹，将枪弹的动量转化为测试系统滑动部分的动量(即动不平衡冲量)。其中枪弹的动量通过高速相机测得的飞行速度乘以弹头质量得到，测试系统滑动部分的动量通过1.1节中的方法得到。同理，可以对传统弹道摆测试方法进行标定，其中弹道摆处理方法参考国家军用标准GJB 349.25—90常规兵器定型试验方法无后坐力炮，具体结果如表1所示。

根据表1中的结果可知，本文给出的动不平衡冲量精确测试系统的测量精度要优于传统弹道摆测试系统，且测试一致性和稳定性都优于传统测试方法。

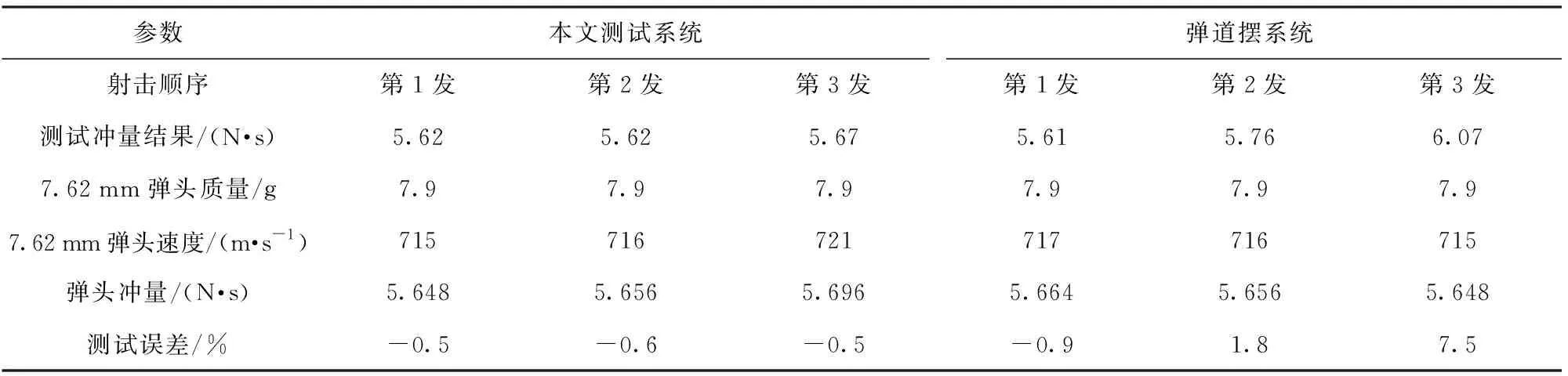
表1 标定结果对比

1.3 试验结果

应用本文提出的测试方法对某轻型无后坐力炮进行动不平衡冲量的测试，并用高速相机监测发射过程和剩余火药燃气的前后喷射情况。某次高速相机拍摄的发射过程中典型时刻结果如图2所示。由于高速相机无法直接拍摄弹底堵片，在发射器喷管出口处放置反光箔片。当弹底堵片开始破坏时，通过高速相机的反复播放即可在电脑上通过反光箔片的反光判断出堵片破裂的时刻，如图2(a)所示；弹底堵片完全破裂时，反光箔片会被完全照亮，如图2(b)所示；弹丸头部出炮口时，由于火药燃气还未在炮口处膨胀，在电脑中经过逐帧播放可以清楚地得到弹丸头部出炮口的时刻，如图2(c)所示；弹带在发射过程中会起到密封作用，因此当弹带出炮口时火药燃气会在炮口处出现泄露膨胀，据此可以得到弹带出炮口的时刻，如图2(d)所示；弹尾飞出炮口时受到炮口火药燃气的遮挡，无法通过图片直接看到，因此需要结合弹丸结构尺寸和图片的像素点位来确定，如图2(e)所示；弹丸飞出炮口复杂流场的时刻可以通过图像直接得到，如图2(f)所示；剩余火药燃气的周期性喷出可以在高速相机图片中清晰地看到，且持续一段时间，截取某一时刻展示如图2(g)所示。

图2 某轻型无后坐力炮发射过程中各典型时刻截图Fig.2 Screenshots of typical moments during launching of a light recoilless rifle

由图2可以看出某轻型无后坐力炮的发射过程如下：内弹道过程以弹底堵片破坏开始到弹丸尾部出炮口结束持续约4.9 ms，后效期以弹带出炮口开始到弹丸飞出炮口复杂流场区域转入外弹道自由飞行结束，持续时间约4.2 ms[15]；在后效期结束后的70 ms左右仍有剩余火药燃气先后从发射器前后喷出，将这一时期定义为轻型无后坐力炮的后后效期，该时期以弹丸飞出炮口复杂流场区域转入外弹道自由飞行开始，到轻型无后坐力炮尾喷管处无明显火药燃气喷射结束。

图3给出了弹道炮膛压测试结果(P1、P3、P4、P5、P7、P8、P9表示不同位置的测压点)，各测压点位置如图4所示，其中P1为药室测压点，该点膛压发生变化的起点认为是发射药点燃内弹道过程开始，其余各点分布于身管的不同位置，直至炮口。根据图3中膛压测试曲线的局部放大图可知，各测压点均在某一相同时刻出现波动，经过分析可知这是弹丸飞出炮口所导致的膛内压力波动，由此很容易判断出内弹道的持续时间在5.0 ms左右，这与高速相机的结果基本一致，表明高速相机记录的发射过程与真实情况是对应的。

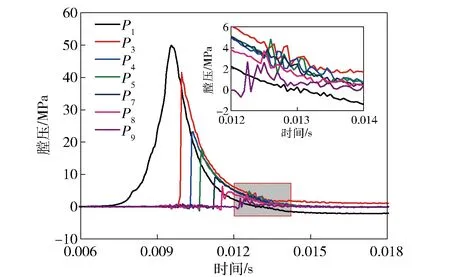
图3 弹道炮膛压测试Fig.3 Chamber pressure of ballistic rifle

图4 弹道炮膛压测试点示意图Fig.4 Schematic diagram of pressure test points in chamber for ballistic rifle

图5和图6所示为自行设计的精密平衡测试系统的测试结果。两图分别给出了轻型无后坐力炮发射常温状态的弹1(杀伤爆破弹)和弹2(攻坚弹)时，发射器的典型原始运动曲线。由图5和图6可以看出，弹丸发射过程中，发射器会在动不平衡力作用下产生一个速度，并在测试系统的滑轨上自由滑动。由于内弹道过程在5 ms左右就结束了，而发射器的运动时间在500 ms左右，忽略发射器的运动加速过程，假设其在内弹道过程结束后瞬间获得一个初速，此后发射器只受到摩擦力及膛内剩余火药燃气的作用。对位移曲线的局部放大区域进行分析可知，发射器在滑轨上的运动包含两部分，一部分是沿滑轨的自由摩擦滑动，另一部分是在滑动的同时存在前后振动，这里的振动是由剩余火药燃气在发射器身管内的速度脉动造成的，该气动振动期即为后后效期。对两种弹丸射击时的曲线振动部分进行测量可知，振动周期均为10 ms左右，且与发射弹种无关。

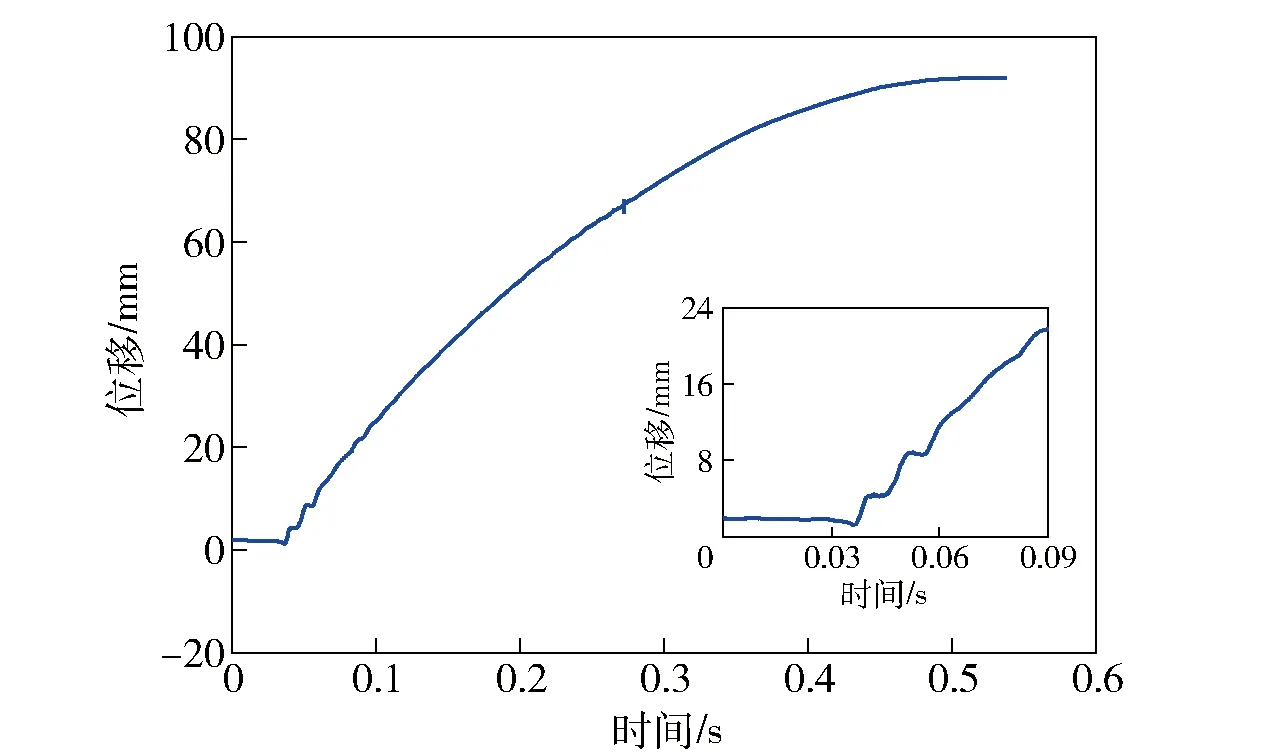
图5 弹1常温动不平衡位移曲线Fig.5 Dynamic unbalance displacement curve of Projectile 1 at room temperature

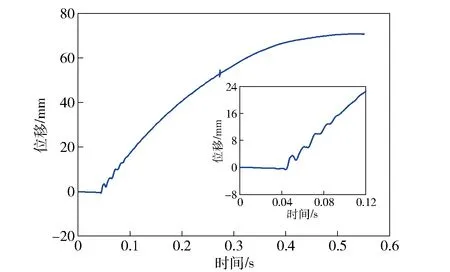
图6 弹2常温动不平衡位移曲线Fig.6 Dynamic unbalance displacement curve of Projectile 2 at room temperature

2 模型与讨论

2.1 建立数学模型

轻型无后坐力炮安装在滑动轨道之上，在弹丸发射的瞬间，由于火药燃气和弹丸的共同作用，发射器会获得一个初速并以该初速为起始条件在滑动轨道上开始运动。此后，由于轨道的限制，以发射器为研究对象进行轴线方向受力分析可知，其在滑动轨道上的运动主要受到两种外力的作用：一种是来自滑动轨道的摩擦力，使发射器做匀减速运动；另一种是来自发射器内剩余火药燃气的周期性往复作用力，使发射器沿轨道做前后振动运动。两种运动是相互叠加在一起的，为了方便模型建立，需要将这两种运动分开讨论，并分别建立相应的动力学模型。

沿轴线的滑动摩擦运动动力学方程为

(1)

式中：μ为滑动摩擦系数；m为发射器质量(在试验中为测试系统滑动部分的总质量，kg)；g为重力加速度；x为发射器位移(mm)；t为发射器运动时间(s)。

由于受到剩余火药燃气周期作用力沿轴线的前后振动，弹丸出膛以后，特别是后效期结束以后，轻型无后坐力炮身管内仍有剩余火药燃气残留。轻型无后坐力炮存在炮口和喷管两个相互对立方向的开放出口，当剩余火药燃气从炮口喷出时，发射器会产生向后的后坐力，当剩余火药燃气从炮尾喷管喷出时，发射器会产生向前的前冲力。根据高速相机记录的情况可知，剩余火药燃气在身管内做周期性往复脉动，因此后坐力和前冲力会周期性的交替产生。由于身管内剩余火药燃气会从炮口和喷管两个开放出口交替喷出，随着时间的推移，每次火药燃气喷出所产生的力会迅速衰减。此时身管的受力情况为方向相反的两个力周期性交替产生，且两个力会随时间推移逐渐减小，直至消失，因此由发射器和身管内剩余火药燃气组成的系统运动规律与振体弹簧阻尼系统的运动规律相似。由此得到该周期运动的动力学方程为

(2)

式中：c为结构阻尼；k为弹簧刚度系数。

2.2 模型的稳定性分析

根据图5和图6的试验曲线可知，发射器沿轨道做滑动摩擦运动，其振动运动趋势逐渐稳定收敛于发射器的滑动轨迹。因此，为了验证本文选取的振动运动模型的适用性，利用范式理论[16]对其渐进稳定性进行分析。

(3)

进而给出弹簧阻尼振动微分方程的范式：

(4)

式中：xv、xd分别为弹簧阻尼系统的速度扰动和位移扰动。

设x0是初始扰动，由x0出发的解是x(t)，则系统的总能量方程(省略t)为

(5)

为了判断弹簧阻尼振动系统的渐近稳定性，将总能量函数增加1项δxvxd，即令判断稳定性的定号函数V(x)为

(6)

式中：δ为代系数。令V(x)=xTCx，则

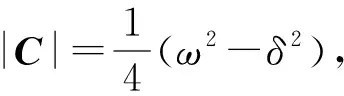
通过(3)式给出V的全导数：

(7)

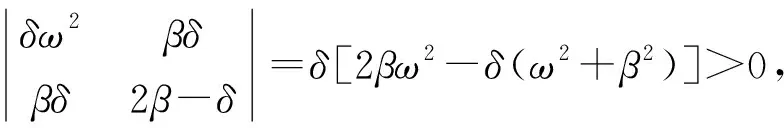
(8)

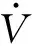
(9)

由于ω>0，β>0，满足条件的δ是存在的，(3)式所表示的弹簧阻尼振动是渐近稳定的。因此，该模型适用于发射器前后振动运动的分析。

2.3 结果讨论

根据2.1节建立的数学模型，分别给出(1)式和(3)式的解。其中：

(1)式的解为

(10)

式中：t0为位移时间偏移量(s)；v0为滑动初速(m/s)；x0为位移的起始偏移量(mm)。

(3)式的通解形式为

x=e-βt(c1cos(Ωt)+c2sin(Ωt))，

(11)

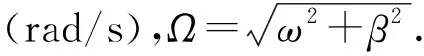
(11)式变换为如下形式：

x=Ae-βtsin(Ωt+φ)，

(12)

(10)式与(12)式相加，即得到发射器在轨道上运动的解为

(13)

式中：t0和x0通过图5和图6中的曲线起始变化点确定；Ω和A通过对图5和图6中曲线波动部分的测量得到。将振动部分的e-βt和φ作为调整量，进行数学模型与试验曲线的符合计算，结果如图7和图8所示。

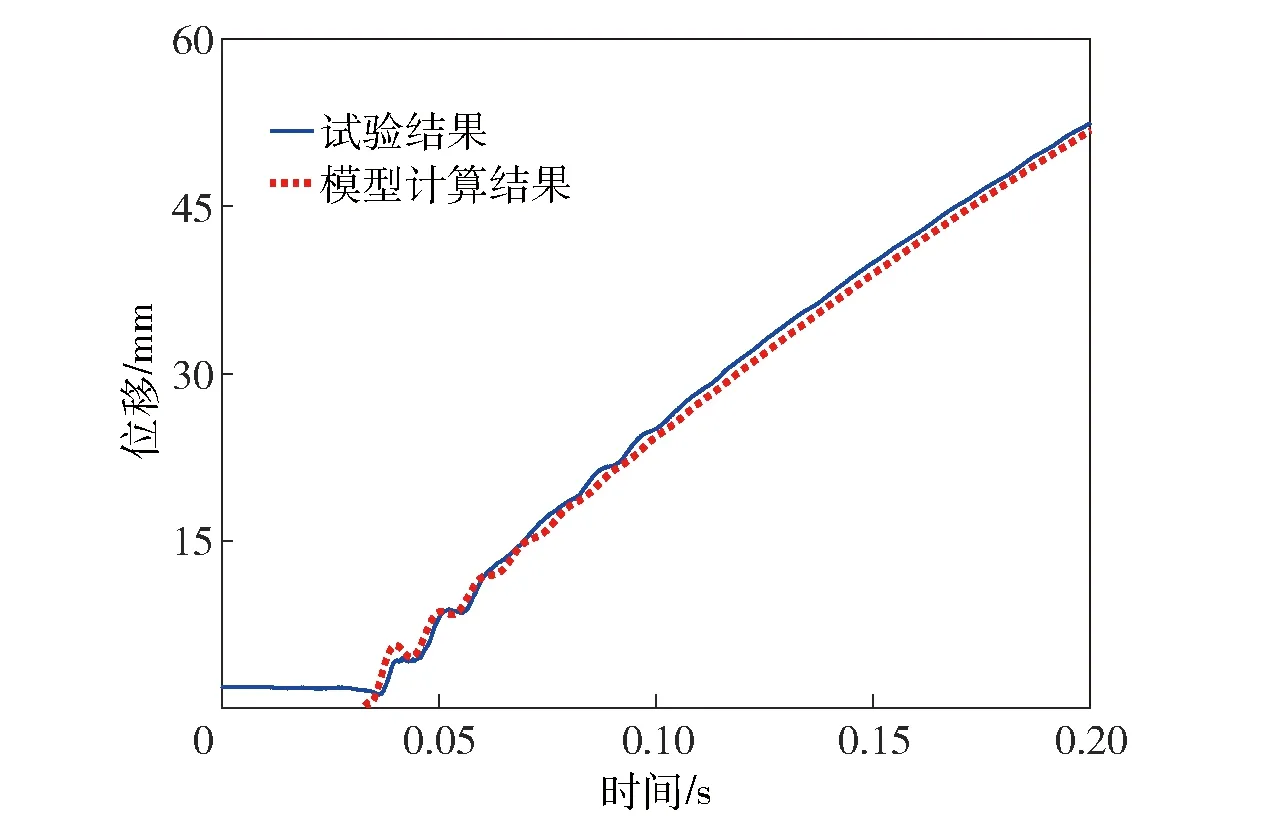
图7 弹1试验曲线与模型计算结果对比Fig.7 Comparison between test result of Projectile 1 and calculated result of model

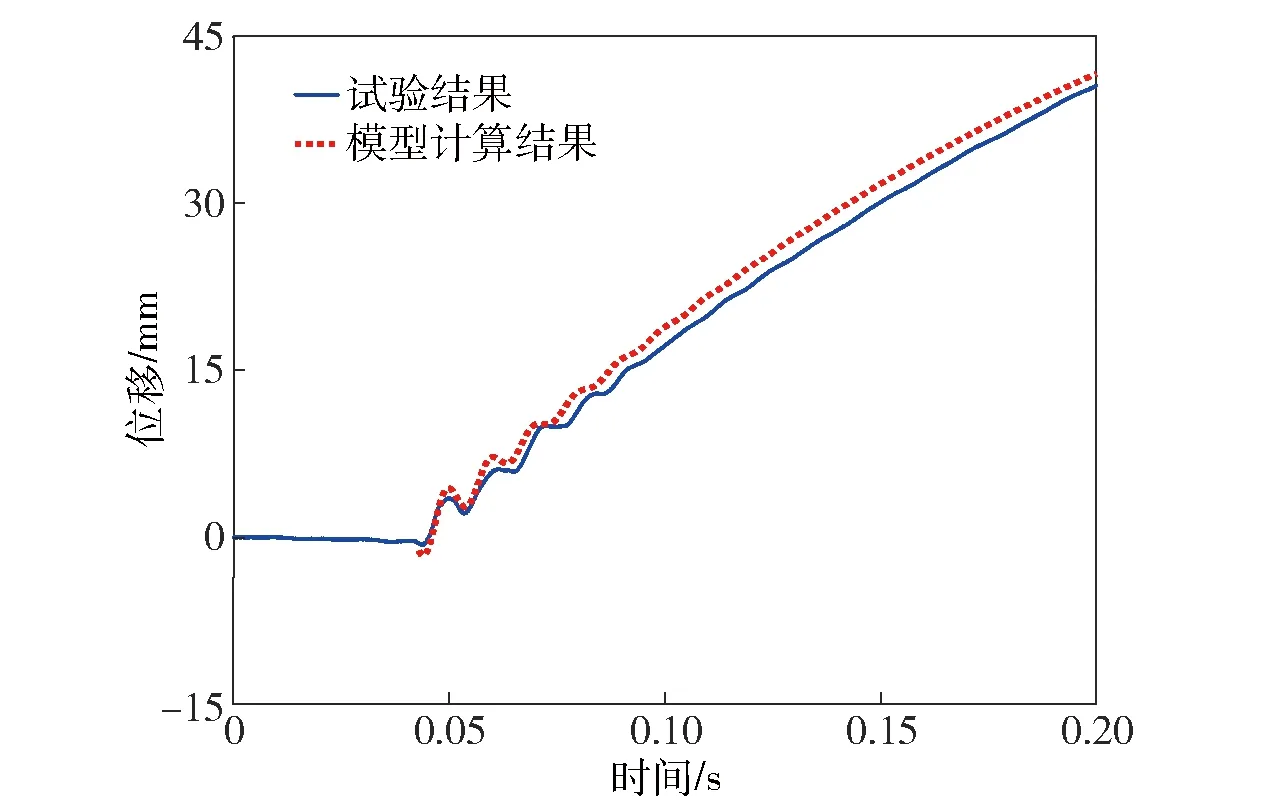
图8 弹2试验曲线与模型计算结果对比Fig.8 Comparison between test result of Projectile 2 and calculated result of model

由图7和图8可以看出，本文建立的数学模型与两个不同弹种的试验结果均具有很好的一致性，该模型反映了轻型无后坐力炮发射过程中后后效期剩余火药燃气对发射器的作用规律。将这一结果进行推广分析可知，发射器在后后效期内由于剩余火药燃气的往复速度脉动作用而在滑轨上产生振动，振动的程度主要与剩余火药燃气的量有关，而剩余火药燃气的量与火药燃烧状态有关。因此，当弹药处于高温状态时，火药燃烧速率加快，在后后效期剩余的火药燃气减少，发射器在滑轨上的振动随之减弱甚至振动消失。反之，当弹药处于低温状态时，火药燃烧速率减慢，在后后效期将会剩余更多的火药燃气，此时发射器在滑轨上的振动就会加剧。极端条件下，低温状态火药出现不稳定燃烧，振动加剧且无衰减趋势，最终可能导致发射器出现低温前冲现象，而这在轻型无后坐力炮的设计中是不被允许的。

图9和图10分别给出了高低温条件下轻型无后坐力炮发射时的动不平衡位移曲线，图11所示为弹2出现不稳定燃烧时发射器前冲的位移曲线，图12所示为弹2出现不稳定燃烧时的膛压曲线。由图9～图12可以看出，试验结果与前文通过模型进行的推广分析结果是一致的。由此可见，后后效期内气动振动引起的不平衡力在轻型无后坐力炮的设计中具有重要意义，需要重点关注。

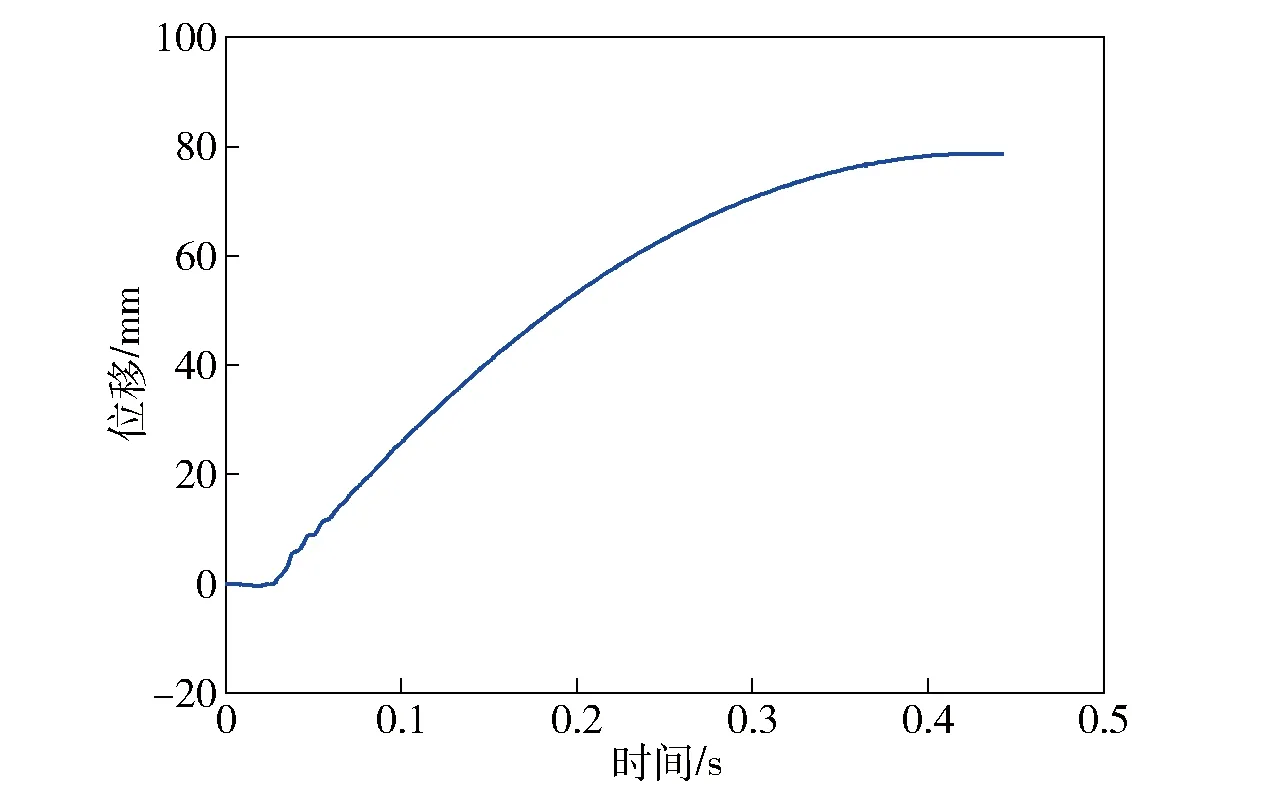
图9 弹2高温动不平衡位移曲线Fig.9 Dynamic unbalance displacement curve of Projectile 2 at high temperature

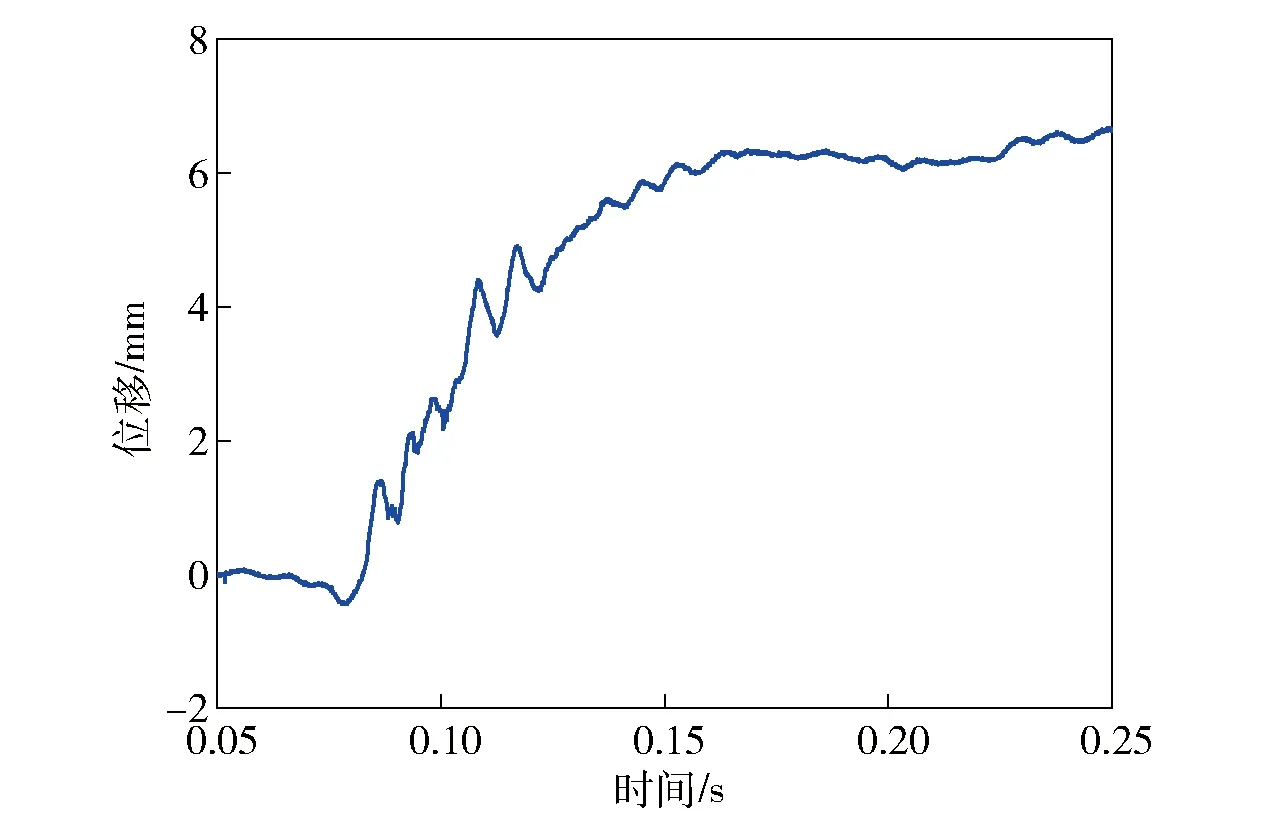
图10 弹2低温动不平衡位移曲线Fig.10 Dynamic unbalance displacement curve of Projectile 2 at low temperature

图11 弹2低温不稳定燃烧时的动不平衡位移曲线Fig.11 Dynamic unbalance displacement curve of Projectile 2 at low temperature unstable combustion

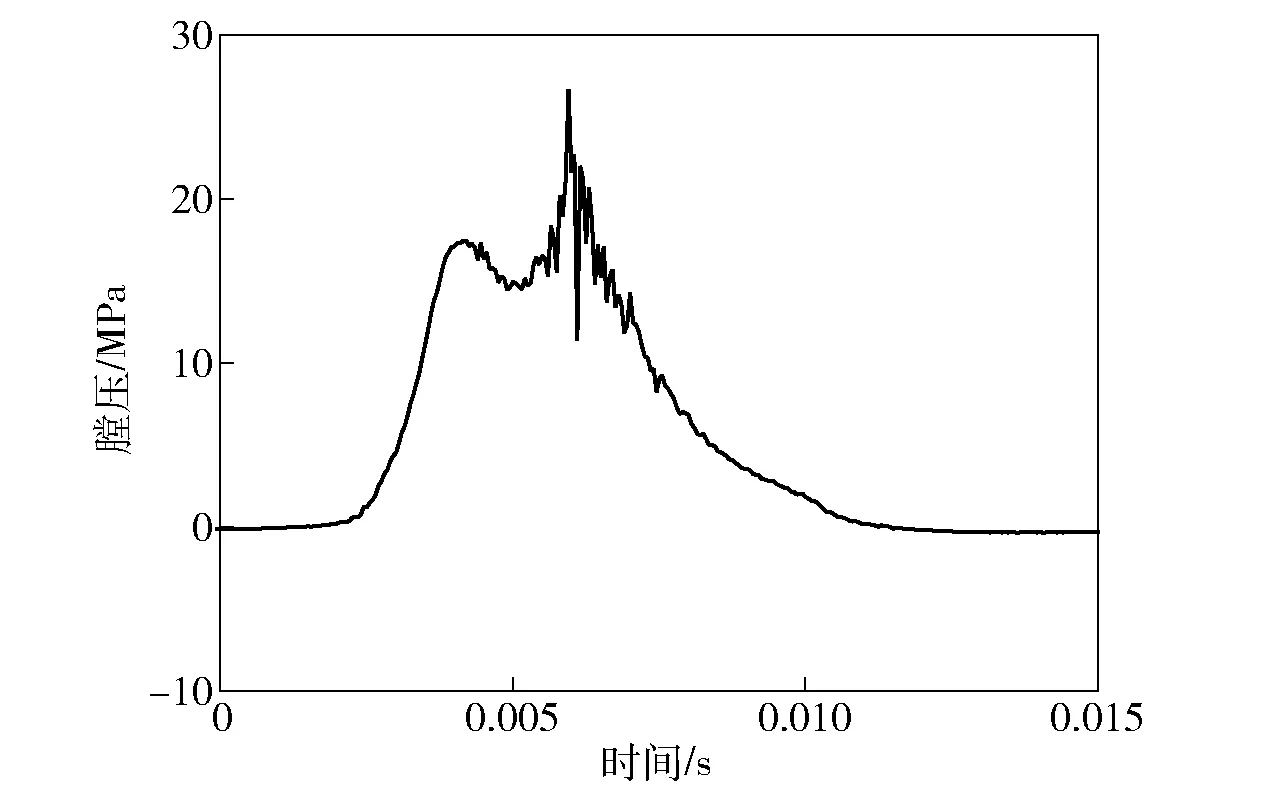
图12 弹2低温不稳定燃烧时的膛压曲线Fig.12 Chamber pressure curve of Projectile 2 at low temperature unstable combustion

3 结论

本文通过自行设计的精密平衡测试系统对某轻型无后坐力炮的动不平衡冲量进行了测试，并根据振动系统运动稳定性理论建立了相关数学模型，对测试结果中的振动现象进行了科学的解释。得到以下主要结论：

1)轻型无后坐力炮由于大量采用轻量化设计，质量轻，剩余火药燃气在后效期结束以后的较长时间内仍对发射器动不平衡有很大影响，由此发现了轻型无后坐力炮的后后效期及该时期在动不平衡设计中的重要作用。

2)振动系统运动稳定性理论可以用于轻型无后坐力炮后后效期剩余火药燃气对发射器动不平衡冲量影响机理的研究。

3)低温条件下火药燃烧不充分，当出现不稳定燃烧时会导致发射器前冲。