政府分摊企业应急生产成本契约模型构建

胡益传， 刘 浪， 陈思仪

（华东交通大学 经济管理学院，南昌 330013）

近年来，我国突发事件频发，如2008 年“汶川大地震”、2017 年“九寨沟地震”等。灾害发生后，应急物资的需求急剧增加，当政府的应急物资无法满足灾区需求时，需要与企业合作，企业和政府作为救灾供应链的决策主体，当双方的个体决策和整体决策不一致时，供应链出现失调，破坏供应链的运行效率和绩效。而契约作为协调供应链的主要方式，对供应链绩效有一定的影响，因此如何制定有效可行的合作契约，使供应链系统的应急物资满足灾区需求的同时，也能使供应链实现协调，成为当前学术界研究的焦点。

应急物资具有需求数量大、不确定性强等特点，决策者往往面临着储备的应急物资无法满足受灾点需求的情况。通常采用市场采购的形式来实现物资补给，及时把充足的救灾物质运送到灾区，减少灾民的生命财产损失，从而实现应急物资的有效供应。同时，考虑由政府和企业构成的两级供应链系统，在市场采购的过程中，企业作为应急物资的供应方，政府作为救灾物质分配的需求方，两者要通过制定合适的供应链契约，构建有效的合作机制，如预先采购[1]，实行应急物资的政企联合储备模式，确保物资及时供应。与本文相关的研究主要集中于市场采购、供应链协调、成本契约三个方面。

在市场采购方面，学者们主要将市场采购与不同的供应链契约形式联系在一起。如张琳等[2-4]研究了不同供应链柔性契约下的政府应急物资采购决策。除柔性契约外，期权契约也是比较常见的供应链契约形式，扈衷权等[5]构建了期权契约下应急物资的政企联合储备模型，认为该模型能够提高供应链的物资储备量；王晶等[6]研究在期权契约条件下多种采购方式的协调优化问题。也有学者研究了非契约形式下的市场采购问题，戴宾等[7]研究了责任供应链中供应链成员的采购策略问题。

有不少学者研究了契约协调供应链的问题。如Chen 等[8]研究了期权契约下的二级供应链协调问题。徐春秋[9]认为只有当零售价格等于期权执行价格时，供应链才能达到协调。Hu 等[10]认为在期权契约中引入联合定价能够协调供应链。Dong等[11]在所研究的问题中发现只有收益共享契约能够协调供应链。Lou 等[12]建立了两阶段供应链模型，证明收益共享契约能够协调供应链。Nie 等[13]提出了数量折扣契约来协调二元供应链。Zhao 等[14]分析了闭环供应链的协调机制。

除以上契约协调供应链外，成本契约也是比较常见的契约方式，成本契约旨在供应链成员间通过协议的形式分摊成本，其也是实现供应链协调的一种有效方式。关于成本契约，已有部分学者在低碳和闭环供应链等方面展开了研究。Xie 等[15]结合收益共享契约和成本契约来协调双渠道闭环供应链。Bai 等[16]在由供应商和零售商组成的两级供应链中，提出了基于收入和促销费用的分摊契约来协调供应链。Yue 等[17]研究了制造商和零售商的广告成本分摊契约对于供应链系统绩效的影响。Ghosh，Shah[18]探讨了制造商和零售商之间的绿色成本分摊机制对绿色产业供应链系统利润的影响。Zhou等[19]研究了减排成本分摊对供应链决策及绩效的影响。刘名武等[20]也研究了低碳供应链的成本分摊协调问题。郝新军[21]结合线上和线下销售，对闭环供应链协调问题进了研究，认为采用成本分摊的补偿契约方式可以实现供应链协调。

梳理上述文献发现,学者们研究了不同契约形式下应急物资采购及契约协调供应链的问题。虽然成本契约研究比较丰富，但主要集中于低碳及闭环供应链中，将成本契约应用在应急物资采购中还未见过。政府分摊企业的应急生产成本，并对企业剩余物资的适当补贴，不仅能够增强双方的合作意愿，还能够提高企业为政府生产应急物资的积极性。因此，作者运用成本契约的方式，构建了基于应急生产成本分摊系数和剩余物资补贴系数的应急供应链协调模型，以寻求救灾成本最低而效果最好的应急路径，确保政府能够满足突发事件发生之后急剧增长的应急物资需求，保障应急物资及时供应。研究结果对成本契约理论的完善和应急物资供应的实践保障提供了依据。

一、问题阐述与模型假设

（一）问题阐述

研究中涉及的应急物资种类具有应急价值高、需求量不确定、占用空间小等特点。如医疗器械、帐篷、药品、水和面包等物资，考虑由政府、企业组成的两级供应链系统，政企双方签订成本契约进行采购合作。灾害发生前，企业需投入额外的应急生产成本，以应对灾害的发生。政府在契约期初先购买一定量的常备物资储存在政府储备库中，并制定采购价格、应急生产成本分摊系数和剩余物资补贴系数；企业在契约期初为政府提供常备物资，并根据政府决策决定最优供应系数和最优的弹性物资供应量；若有灾害在契约期内发生，政府首先利用常备物资，若此部分物资无法满足灾区需求，则以采购价格购买由企业储存的弹性物资。若政企双方的物资储存总量都无法满足灾区需求，剩余的物资量在现货市场进行采购。若契约期内无灾害发生，或者有灾害发生且存在剩余物资，两者则按照相同的出售价格出售剩余物资，获取残值收益。同时，政府给予企业一定的剩余资补贴及应急生产成本的适度分摊，两者在协议期末结算。

（二）模型假设

为使模型更具合理性和便于运算，故作出如下假设：第一，为研究成本契约下政府的采购策略保障应急物资供应，假设政府不以行政手段从生产企业获取应急物资，即不能强制企业为其提供物资。第二，应急物资的需求量服从均匀分布。第三，生产企业和政府是理性经济人，且风险是中性的，两者信息对称。第四，企业在生产期内，单位应急物资的应急生产成本是一个常量。

二、数学模型

（一）无成本契约的供应链决策模型

1. 分散决策下的供应链模型

分散决策形式下，政府未与生产企业签订协议，只会从企业处以批发价格 ω批发Qc单位的常备物资，并存储在政府储备库中。设x为应急物资实际需求量。F(x),f(x)分别为物资需求量的分布函数和概率密度函数，c为企业单位物资的固定生产成本，cs为单位剩余物资的处理成本，cτ为单位剩余物资的出售成本，cr为单位应急物资的缺货成本（现货市场价格），ct为企业的单位应急生产成本，此成本可看成是企业为了尽快生产出应急物资而投入的额外人力、机器、资金等成本，Hs,Hg分别为生产企业和政府单位应急物资的库存和管理成本， ∆c为企业单位物资的包装成本，D为物资最大需求量，分散决策下系统的应急物资储备量为Qt。不失一般性，对相关参数进行约束，pm>cs，保证协议期末政企双方出售剩余物资的净收益为正。c+Hs−pm>0，若企业生产和库存成本小于残值收益，那么企业出售剩余物资就能获益，不能保证企业供应物资给政府。设分散决策下企业收益、政府成本及系统成本分别为 πms，Cmg，C1，其表达式分别如式（1）、式（2）和式（3）所示，Qc=Qt。

对式（2）关于政府常规物资储备量Qt的一阶导数和二阶导数，得：

将其代入到式（2）可以求出分散决策形式下政府的最小成本。

2. 集中决策下的供应链模型

集中决策形式下，双方决策的目的是寻求系统成本最低的储备方案，在满足灾区需求的同时，实现供应链整体成本最小化。供应链系统总成本包括政府常规储备物资的固定生产和包装成本及库存成本、企业储备物资的固定生产和包装成本及库存成本。设Qr，Qs分别为集中决策形式下企业的物资储备量和系统的物资储备量。设集中决策下的系统成本为C2，则集中决策下系统总成本为：

通过对式（6）关于集中决策下生产企业应急物资储备量Qr求一阶导数和二阶导数，得：

由可知，集中决策下的系统总成本能够取到最小值，令式（7）等于零，可以得到集中决策形式下生产企业最优储备量Qr∗，如式（9）所示。

因此，集中决策下系统的最优应急物资储备量为：

（二）政府分摊企业应急生产成本的供应链成员决策模型

本小节假设政企双方都是理性经济人，政府作为Stackelberg 博弈的领导者，考虑作出决策后企业的反应来制定采购决策，企业作为跟随者需考虑政府的决策后再决定其行为。为了求出政企双方的最优策略，采用逆序求解法，先求出企业的最优决策，将其代入到政府的成本函数，进而求出政府的采购决策。下面分别分析生产企业和政府的决策规则，以及在成本契约下如何协调应急供应链的问题。

1. 生产企业决策规则

企业在追求利润最大化的基础上，考虑自身生产水平及相关参数约束，根据政府需要和契约规定向政府提供弹性物资 (αQc)，并制定弹性物资供应系数 α，设p为成本契约下政府单位弹性物资的采购价格， ϕ为政府对企业单位应急生产成本的分摊系数，ϕ ∈[0,1]， λ为剩余物资补贴系数，λ ∈[0,1]。g为政府给予生产企业单位未采购物资的补贴，此部分可看成是政府对企业生产、处理和出售物资等成本的补贴，g=λ(c−pm+cs+cτ)。在成本契约下，设企业的收益函数为 πds，其表达式如式（11）所示。cr⩾p>pm+g−cs−cτ，若缺货成本小于采购价格，那么政府可能不会从企业采购物资，而直接从现货市场进行购买。

将式（11）进行化简得到企业收益如式（12）所示。

对式（12）关于α 求一阶导数和二阶导数，得

式（14）为负说明企业收益函数为弹性物资供应系数的凹函数，存在使企业收益最大的最优供应系数 α∗，通过令式（13）等于零可求得企业最优的供应系数决策，如式（15）所示。

由最优弹性物资供应系数，得到企业在成本契约合作下的最优弹性物资储备量，如式（16）所示。

命题1 当政企之间进行成本契约合作时，政府制定的应急生产成本分摊系数越大，企业最优应急物资的储备量越高。

证明 当政府常规物资不足以满足灾区需求时，政企之间需要契约合作，此时

那么，对q∗关于 ϕ求一阶导，得

由命题1 可知，在成本契约下，当政府制定的应急生产成本分摊系数较高时，即政府承担企业的应急生产成本较大时，可提高企业为政府生产并储备应急物资的积极性，从而当灾害发生时，政府能够有效地向灾区运送应急物资。

2.政府决策规则

政府在估计企业对其供应的最优应急物资数量决策形式后，根据自身的成本水平，以追求成本最小化为目标，设定剩余物资补贴系数 λ、采购价格p和应急生产成本分摊系数 ϕ。政府的成本函数如式（19）所示。

对式（19）进行化简，得到政府成本函数如式（20）所示，其中α 如式（15）所示。

（三）成本契约的供应链协调

由供应链协调的定义可知，当供应链成员的个体决策与整体决策达到一致时，供应链系统的成本等于集中决策下的成本，供应链实现了协调，此时政企双方的总成本将达到最小值。由于因此分散决策形式下无法实现供应链协调。

当政府常规采购量足以满足灾区需求时，政企无需与企业合作，当政府常备物资不足以满足灾区需求时，此时政企需签订成本契约开展合作，下面将考虑成本契约来协调应急供应链。

命题2 在成本契约下，当

时，政企双方签订成本契约进行合作能够实现供应链协调。

证毕。

政企进行契约合作，不仅要考虑到供应链系统经济效益最大化，还要实现合作双赢的目的，即政企双方引入成本契约能够使政府成本有所减小，企业利润有所增加。设政府成本增量为∆Cg，设企业收益增量为∆πs，得到政府成本差值和生产企业利润差值如式（22）和式（23）所示。

命题3 在成本契约下，当剩余物资补贴系数λ ∈[ξ1, ξ2]，应急生产成本分摊系数ϕ ∈[0,min(η1,η2)]时，协调后的应急供应链实现了Pareto 改进。

证明 为研究成本契约对政府成本的影响，对比成本契约前后政府的成本模型，得：

可得：

为了研究成本契约对企业收益的影响，对比成本契约前后企业的收益模型，得：

证毕。

三、数值分析

（一）参数设置与数值计算

当地政府与某一定点企业签订了成本契约，确保企业在非常规突发事件发生之后，按契约规定向政府提供应急物资，参数设置如下：pm=8，cs=2，cτ=1，cr=65，ct=2，θ=0.6，c=20，∆c=2，ω=50，Hs=2，Hg=1，Qc=5000，D=20 000，（价格单位为：元/件，数量单位为：件）。应急物资需求量服从[0，20 000]的均匀分布[22]。运用Matlab 2017a 仿真计算，结果显示：企业最优弹性物资供应系数约为0.67，供应链系统最优应急物资储备量约8333 件，其中5000 件由政府常规储备，剩余的3333 件通过成本契约合作由企业储存。供应链协调下，成本契约的系统成本约为322 500 元，在分散决策形式下，供应商收益为130 000 元，政府成本为462 500元，分散决策下系统成本为332 500 元，可见，通过成本契约实现供应链协调后供应链节约成本约10 000 元。应急供应链协调下的政府各项决策关系如图1 所示，具体数值分析结果如表1 所示，选取表1 中的剩余物资补贴系数分别为0.42 和0.62，进行政企成本收益分析，政企成本收益变化如图2所示。

图1 的结果分析：采购价格与剩余物资补贴系数和应急生产成本分摊系数均呈反向关系，这是符合客观现实的。因为在剩余物资补贴系数不变时，政府制定的应急生产成本分摊系数越高，导致政府承担的应急生产成本增加，那么政府会适当降低采购价格来保护自身利益；当应急生产成本分摊系数不变时，政府制定的剩余物资补贴系数越高，支付的补贴较高，政府同样会降低采购价格保护自身利益。

图2 的结果分析：当采购价格很高且应急生产成本分摊系数很高时，企业利润将变得很高，此时对政府是不利的，双方引入成本分摊契约不能实现供应链协调，当采购价格很低且应急生产成本分摊系数很低时，政府成本增量变得很低，此时对企业是不利的，双方引入成本分摊契约也不能实现供应链协调；此外，当 λ=0.42 时的政府成本增量值是大于 λ=0.62 的政府成本增量值，即剩余物资补贴系数越大，政府获得的系统节约成本越多。这与表1的数值分析结果是一致的。

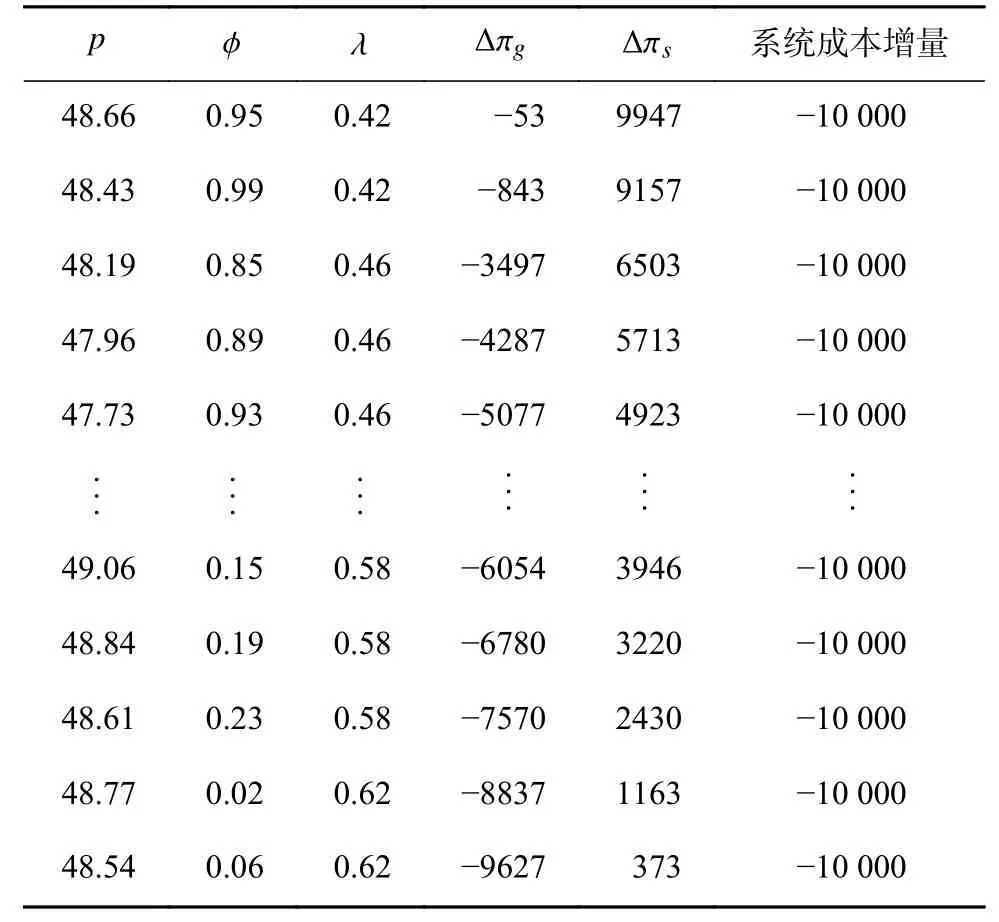
表 1 供应链协调下政府决策变化对政企双方收益的影响

表1 的结果分析：在同一剩余物资补贴系数水平下，政府在契约期初能够以较低的采购价格购买常规物资，缩小自身成本，那么政府将会获得较多的系统节约成本；当政府制定的应急生产成本分摊系数较低时，采购价格较高，此时企业可以通过向政府销售常规应急物资来获得较多的利润；当政府剩余物资补贴系数制定地较高时，可以通过制定较低的应急生产成本分摊系数来控制自身成本，例如当 ϕ=0.02 时，政府可以设定 λ=0.62 以获得较多的系统节约成本，并且剩余物资补贴系数越高，政府获得的系统节约成本越高。因此，在同一剩余物资补贴水平下，政府可以通过提高应急生产成本分摊系数降低采购价格，进而获得更多的节约成本，在不同剩余物资补贴水平下，当剩余物资补贴水平较高时，政府可以降低应急生产成本分摊系数，从而减少政府承担企业的应急生产成本，进而获得更多的节约成本。

结 论

灾害发生的不可预测性和物资需求的不确定性需要政企双方达成合作，企业能够在灾害发生之后按照契约规定向政府提供物资，由于地方灾害随时可能发生，企业需要提前生产并储备应急物资，当灾害发生时，能够尽快地满足灾区需求。基于此，研究中考虑企业生产单位物资所产生的应急生产成本和生产周期长、占用库存空间小的瓶装水、药品和面包等紧急物资，构建了基于应急生产成本分摊系数和剩余物资补贴系数的成本契约模型，使用逆序求解法，求得双方的最优决策，证明了成本契约能够协调应急供应链并得出实现供应链协调的条件，协调后的供应链实现了Pareto 改进。

研究可得到如下几点管理启示：1)与分散决策形式相比，成本契约合作能够使系统成本降低，且能够使政企双方实现双赢的目的；2)政府采购价格与应急生产成本分摊系数和剩余物资补贴系数均呈反向关系，在同一剩余物资补贴水平下，政府可以通过提高应急生产成本分摊系数降低采购价格，进而获得更多的节约成本，在不同剩余物资补贴系数下，当该系数制定较高时，政府可以制定很低的应急生产成本分摊系数来获得更高的节约成本；3)政府若以较低的采购价格采购应急物资，考虑供应链系统收益和为了使合作顺利进行，应该对企业的应急生产成本进行适当分摊，从而增强企业生产并储备应急物资的积极性，扩大双方的合作意愿。整体上而言，研究结果对应急物资采购提供了一定参考价值和建设性管理意见，丰富了成本契约理论。后面可把成本契约结合其他契约作为未来的重点研究方向之一。