聚焦反比例函数，探究综合性问题

沈习辉

[摘  要] 中考对反比例函数内容的考查常以综合题的形式进行，因此深入探究反比例函数的知识及常见综合形式十分必要. 文章结合2020年江苏省中考反比例函数综合题开展问题解析、方法探究，以期对读者有所帮助.

[关键词] 反比例函数;图像;性质;几何;面积

反比例函数是初中数学的重要内容，其知识内容同数与式、方程、不等式、几何图形、三角函数等联系紧密，是初高中知识的重要衔接部分. 中考对其的考查形式较为灵活，除了注重基础知识外，还常与关联知识相综合，需要学生联系知识考点，全方位审视问题.

■ 与一次函数综合，考查函数性质

反比例函数是初中函数的重要組成部分. 在初中阶段，需要掌握一次函数、反比例函数、二次函数的性质与图像. 反比例函数与一次函数的综合题在中考中最为常见，解析问题时需要把握两种函数的性质，以图像交点为突破口构建解析方程，分析图像的位置关系.

例1（2020年泰州市中考数学卷第16题）如图1，点P在反比例函数y=■的图像上，且横坐标为1，过点P作两条坐标轴的平行线，与反比例函数y=■ （k<0）的图像相交于A，B两点，则直线AB与x轴所夹锐角的正切值为______.

解析 因为点P在反比例函数y=■的图像上，且横坐标为1，所以点P的坐标为（1，3）. 根据题意过点P分别作x轴和y轴的平行线，连接AB，如图2. 由题意易得点A的坐标为■ ，3，点B的坐标为（1，k）. 则直线AB与x轴所成锐角可放在Rt△ABP中，其正切值可表示为■=■=3，所以所求正切值为3.

■ 以几何动点为载体，考查函数

解析式

反比例函数与几何动点结合是中考的重要综合形式，常以反比例函数图像为背景，设定相关动点，以几何运动为载体构建模型，能全面考查反比例函数k的意义及解析式. 解析问题时，应化“动”为“静”，立足曲线相交，借助方程确定交点坐标.

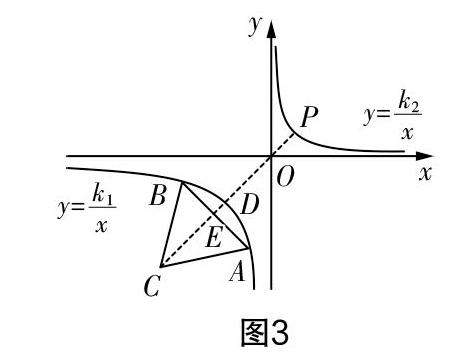
例2  （2020年淮安市中考数学卷第16题）如图3，等腰三角形ABC的两个顶点A（-1，-4），B（-4，-1）均在反比例函数y=■（x<0）的图像上，AC=BC. 过点C作边AB的垂线交反比例函数y=■（x<0）的图像于点D，动点P从点D出发，沿射线CD方向运动3■个单位长度，到达反比例函数y=■（x>0）图像上一点，则k■的值为______.

解析  设AB与CD的交点为E. 分析可知△ABC为等腰三角形，CD为AB的垂直平分线，所以CD为反比例函数y=■（x<0）的对称轴. 所以直线CD的解析式为y=x. 由于点A的坐标为（-1，-4），其在y=■（x<0）的图像上，所以k■=4. 又直线CD与y=■（x<0）的交点为D，所以可解得点D的坐标为（-2，-2）. 所以OD=2■. 点P从点D出发，沿射线CD运动3■个单位长度到达反比例函数y=■（x>0）的图像上，则OP=■. 所以点P的坐标为（1，1）. 将其坐标代入y=■（x>0）中，解得k■的值为1.

■ 与不等式知识相联系，考查数

式图像转化

反比例函数具有数式的特点，可用于研究方程、不等式的数量关系. 深入理解函数与不等式、数式之间的关系，有助于建立整个数学体系. 中考对该部分的考查除了注重对函数与数式、不等式关系的研究外，还侧重考查数式图像之间的转化，如反比例函数、方程的解、数轴之间的转化.

例3  （2020年南京市中考数学卷第20题）已知反比例函数y=■的图像经过点（-2，-1）.

（1）求k的值.

（2）完成下面的解答.

解不等式组：2-x>1①■>1②

解：解不等式①，得______.

根据函数y=■的图像，得不等式②的解集为______.

把不等式①和②的解集在数轴上（图4）表示出来.

从中可以找出两个不等式解集的公共部分，得不等式组的解集为__________.

解析？摇 （1）因为点（-2，-1）在反比例函数y=■的图像上，所以k=2.

（2）解不等式①，可得x<1. 由反比例函数y=■的图像可知不等式②的解集为0

■ 与几何最值相综合，考查面积

模型

反比例函数与几何联系紧密，中考常联系三角形考查面积，有时还会涉及几何最值，能同时考查二次函数的性质. 该类问题的突破需分三步进行：第一步，解析图像;第二步，构建面积模型;第三步，完成面积最值分析.

例4  （2020年连云港市中考数学卷第24题）如图6，在平面直角坐标系xOy中，反比例函数y=■ （x>0）的图像经过点A4，■，点B在y轴的负半轴上，AB交x轴于点C，C为线段AB的中点.

（1）m=________，点C的坐标为________;

（2）若点D为线段AB上的一个动点，过点D作DE∥y轴，交反比例函数的图像于点E，求△ODE面积的最大值.

解析  （1）将4，■代入反比例函数y=■（x>0）中，可解得m=6. 由于点A和点B的横坐标分别为4和0，利用中点坐标公式可求得点C的横坐标为2，所以点C的坐标为（2，0）.

（2）设直线AB的解析式为y=kx+b，代入点A和点C的坐标后可求得直线AB的解析式为y=■x-■. 由条件设点D的坐标为a，■a-■（0

■ 反思总结

中考对反比例函数内容的考查常以知识综合的形式进行，涉及一次函数、几何图形、动点运动、不等式组、图形面积、最值探究等知识，问题形式多样，充分把握对应知识的定理定义，逐步转化分析，构建条件与结论之间的关系是突破的关键. 对于一些命题形式较为抽象的问题，建议采用数形结合的分析方法，合理添加辅助线构建问题模型，通过直观的图像来降低思维难度.

在教学实践中，建议教师从与反比例函数相关联的知识入手，把握函数的数式特点、图形特点，准确定位函数的思想内涵，然后把握知识的联系点，引导学生全方位地解析反比例函数，探究综合性问题的解析思路，拓展学生的数学思维. 由于综合题所涉及的数学方法较多，所以教学中教师需注意总结常见问题的解法，如待定系数法、中点坐标公式法、点与直线的距离法、函数性质分析法等，帮助学生强化类型问题的解析方法，使学生形成反比例函数综合题的解题策略.