失水事故引起反应堆堆内结构动响应分析的声学有限元方法

赵燮霖 马英超 叶献辉 姜乃斌 周进雄

1（西安交通大学航天航空学院机械振动与强度国家重点实验室 西安 710049）

2（中国核动力研究设计院核反应堆系统设计技术重点实验室 成都 610200）

大破口失水事故（Large-break Loss-of-coolant Accident，LB-LOCA）是核反应堆结构设计中必须要考虑的一种极限情况。失水事故引起从破口到反应堆内部泄压波的传播，引起吊篮等结构的流固耦合振动。导致连接件松动、结构动应力过大而破坏，因此评估堆内结构由于失水事故引起的动响应具有重要意义。

在核反应堆结构力学领域对大破口失水事故引起的堆内结构动响应分析始于20世纪60～70年代，特别是1979年美国三哩岛核电站失水事故引起了人们对这一问题的进一步关注。早期开展的研究如Au-Yang等［1-2］认为流体的影响仅表现为一种附加水动力质量，给出了一种纯结构力学的求解方程，由于忽略了流固耦合作用，此种求解方法的精度不高。同时期也有不少研究机构，用内部开发的流体力学和结构有限元分析软件，进行单向或双向流固耦合分析计算，但由于软件缺乏通用性，分析结构之间差异较大且高度依赖于研究机构的工程设计经验。近年来，随着计算机软件硬件水平的飞速发展，特别是大型通用CAE（Computer Aided Engineering）计算机辅助工程软件在核工程领域的推广和应用，研究者开展了基于计算流体动力学（Computation Fluid Dynamics，CFD）的单向/双向流固耦合LOCA事故分析。Hermansky等［3］采用MSC.Dytran有限元软件对 LOCA 动态响应进行数值模拟；Nilsson［4］利用ADINA采用三种不同的方法对HDR V31.1实验进行数值模拟，并对比了计算成本；Sheykhi等［5-6］编制相应计算程序并结合ABAQUS对于不同反应堆压力容器在LOCA事故下的压力极值与应力分布进行了预测；Brandt等［7］采用管理MpCCI软件管理流固数据传递，基于Fluent和Abaqus对HDR（Heiss Dampf Reaktor）实验LOCA实验进行了数值模拟。这些基于CFD的LOCA动响应分析，可以使流体力计算更加精确，依赖商用软件的耦合功能或第三方数据通讯交换软件的功能，使LOCA动响应的分析模型从早期的梁模型发展到三维复杂堆内结构建模和仿真，大大提高了处理复杂工程实际问题的能力，但同时也显著增加了计算成本和设计分析周期。

在LOCA动响应分析方法中，与基于CFD的分析方法并行的另一种方法是基于势流体的声学有限元方法。相比于精确的CFD计算，势流体声学方法忽略了流体的粘性，无须求解速度场，流体动量方程退化为简单的声波方程。Bathe等［8-10］提出了基于位移的声学有限元方法求解流固耦合问题，基本变量为流体和固体的位移和流体压力，非常适合用于有限元法求解，使得流固耦合数值计算得到简化。此外 Luke［11］与 Kähkönen［12］以 及 Sussman 与Sundqvist［13］也开展了类似的基于声学有限元方法的LOCA动响应研究。上述这些研究大都基于用户自己编制的有限元程序，适用性和通用性有一定的局限性。本文基于ADINA软件开展了基于声学有限元的LOCA动响应分析，通过与德国HDR实验反应堆V32破口失水事故实验结果和基于ADINA软件的CFD双向流固耦合结果对比，表明声学有限元方法用于模拟德国HDR实验反应堆V32破口失水事故的动响应是可行的。

1 基于位移的声学有限元理论

一般的流体力学理论其基本的变量为速度、密度、压力和温度。采用有限差分法或有限体积法求解。而ADINA采用的是Bathe等［8-10］提出的基于位移的势流体理论，采用有限元法求解，这样就和以位移为基本变量的固体有限元方法实现求解策略的无缝衔接，这也是ADINA流固耦合分析技术的优势和特色之一。参考文献［8-10］，基于位移的声学有限元理论概述如下：

假设流体无粘、可压缩、无旋，声压及位移、速度都是变量，则流体的控制方程如下：

其中：式（1）为连续性方程，式（2）为势流体忽略重力下的动量方程，也称为Euler方程。式中：ρ为流体密度；V为流体质点速度；p为流体质点的压力。

式（1）、（2）为传统的以速度、密度、压力为基本未知量的流体力学方程。针对势流体声学有限元求解策略，可以将上述方程转化为以位移和压力为基本变量的方程。定义，其中：c为势流体的声速；U为流体质点的位移，则连续性方程（1）两边同时对时间积分得到：

而动量方程（2）则简单改写为：

式（3）和（4）即为以位移、压力为基本未知量的势流体有限元基本方程。固体的平衡方程为：

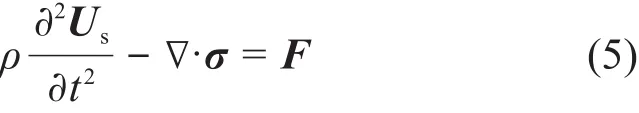
式中：Us为结构的位移；F为载荷矢量，包括流固耦合作用力；σ为结构的应力。式（3）～（5）并加上固体的本构方程，就构成了以流体/固体位移、流体压力为基本未知量的流固耦合方程，可以很方便地采用有限元法进行离散和求解，具体细节可参考Bathe等的文献［14-16］。

2 计算模型与结果分析讨论

图1给出了德国HDR实验反应堆的结构图。本文主要针对V32实验［17-18］，破口位于降压管口位置，反应堆其他管口在实验中都处于封闭状态。HDR实验堆主要考虑失水事故引起的堆内吊篮的动响应，其余结构都作了简化处理，堆内结构对动响应的影响通过吊篮下方的质量环进行模拟，吊篮下端自由，上端刚性连接于压力容器内壁上。

图1 HDR压力容器结构图Fig.1 Structural drawing of pressure vessel of HDR

图2 给出了计算所采用的流体及固体域网格，网格由Hypermesh生成，经过网格无关解检验，最终确定流体域网格6.4万，固体域网格4.5万。固体域采用实体单元，流体域采用3D亚声速流体单元。流固界面处网格共节点。破口压力边界条件施加简化了HDR实验中传感器实测的压力值，初始时刻冷却剂 压 力 11 MPa，在 1 ms内 骤 降 8.75 MPa，在1～1.5 ms内压力回升0.75 MPa，在1.5 ms后破口压力维持在3 MPa。

图2 HDR流体区域(a)和固体区域(b)模型网格Fig.2 HDR meshes of fluid region(a)and solid region(b)

声学有限元计算所用参数如下：流体密度ρ0=730 kg·m-3，体积压缩模量k=8.202×108Pa；固体材料密度ρ=7 800 kg·m-3，线弹性材料杨氏模量E=1.75×1011Pa，泊松比v=0.3。声学有限元采用ADINA9.4中的ADINAstructures模块，求解器采用隐式动力学求解，Newmark积分方法。为了与声学有限元计算结构对比，同时开展了基于CFD的双向流固耦合模拟，流体采用可压缩层流模型，流体动力粘度系数μ=0.000 01 kg·m-3，流固交界面定义流固耦合边界条件。

图3给出了不同时刻下流体压力分布云图，可以看出破口失水事故引起流体域内压力波的传播过程。图4给出了由于波传播导致的反应堆结构位移云图，可以看出由于泄压波在流域内的传播，对浸没在流体域的吊篮施加交变的压力，导致吊篮产生摇摆振动。

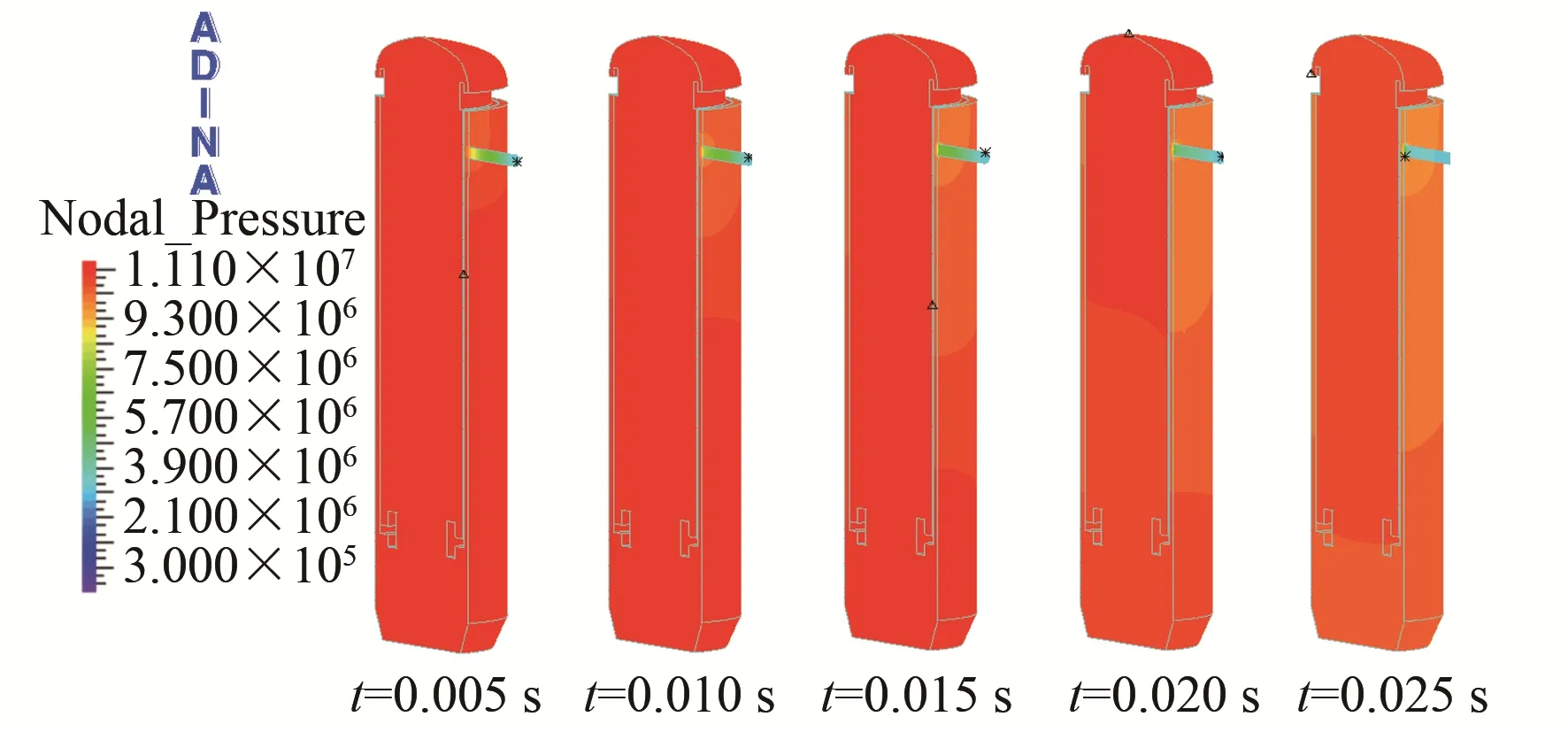
图3 不同时刻下流体区域压力分布云图Fig.3 Plots of pressure contours at selected instants of time

图4 不同时刻下固体区域位移分布云图Fig.4 Plots of displacement contours at selected instants of time

为了进一步验证所采用的声学有限元计算结果，图5给出了破口下方1.7 m高度处吊篮与压力容器之间的径向位移差，图6给出了破口高度处（8.85 m）吊篮外壁的轴向应变。可以看出，基于声学有限元方法和基于CFD双向流固耦合计算方法所预测的径向位移差与轴向应变较实验测试结果吻合良好，相比于声学有限元方法基于CFD双向流固耦合计算方法给出的曲线更加光滑，这与已有文献中的结果一致［13］。相比于CFD方法，声学有限元方法计算效率较高，采用配置了4核i7CPU 3.6 Hz处理器的工作站进行并行计算，声学有限元方法计算耗时3 h 46 min，CFD流固耦合方法耗时5 h 16 min。

图5 破口下方1.7 m处吊篮与RPV相对径向位移之差Fig.5 Relative radial displacement between the core barrel and RPV under blowdown nozzle 1.7 m

图6 吊篮外壁在破口高度（8.85 m）处轴向应变Fig.6 Axial strain on the outer surface of the core barrel at height of blowdown nozzle(8.85 m)

3 结语

基于有限元软件ADINA中的势流流体模块，对德国HDR实验反应堆V32破口失水事故实验进行了声和结构双向耦合数值模拟，结果表明：声学有限元模型计算结果与CFD双向流固耦合以及实验结果吻合良好。由于声学有限元计算方法只需要求解声波方程而无需求解复杂的NS方程，因此较CFD流固耦合方法的计算效率略高。反应堆破口失水事故过程中冷却剂的压力波包含由破口压降导致的入射波和由于固体位移引起的诱发波，诱发波满足小振幅假设，因此这类短时瞬态问题适合用声学有限元求解。但势流模型不包含流体粘性，因而用于长时程动响应分析时要慎重。