医用直线加速器入射电子束能量的快速模拟确定

韩俊杰 庄永东 刘小伟

1（广东省人民医院放疗科 广州 510080）

2（中山大学物理学院 广州 510275）

蒙特卡罗（Monte Carlo，MC）算法能够模拟内照射源或外照射源的粒子输运过程，并且紧接着追踪粒子在感兴趣组织内的输运和能量沉积。蒙特卡罗方法为放射治疗中粒子输运的模拟提供强有力的工具［1］。随着计算机计算速度的提高和MC代码的完善，人们利用蒙特卡罗方法针对医用直线加速器展开了各种各样的研究［2-7］。

利用蒙特卡罗方法模拟医用直线加速器时，首先向厂家获取医用直线加速器机头的几何参数和材料参数，而后基于这些参数，建立医用直线加速器的蒙特卡罗模型；模拟时，还需要设置入射电子束的打靶参数。而入射电子束的打靶参数是正确建立加速器模型的关键，然而确定入射电子束的打靶参数是一个反复耗时的过程。对于入射电子束打靶参数的调试，已经有不少报道［8-13］，但是对于调试过程中，如何快速地确定打靶参数则描述较少。

蒙特卡罗模拟时，需要调试的入射电子束参数主要包括如下4个：1）入射电子打靶平均能量（Mean Energy，Eav）；2）能 谱 半 高 宽（Energy Spectrum Full width at Half Maximum，FWHM）；3）电子束宽半高宽（Beam Radius，R）；4）电子打靶角度歧离（Angular Divergence，θ）。

其中对于电子束宽R的调试：Varian推荐的电子束分布为半高宽为0.1 cm的高斯分布，Daryoush等［11］通过模拟Varian 、Elekta和Siemens系列共计9种不同的医用直线加速器后，推荐入射电子束的径向分布为高斯分布，其半高宽设置最好接近0.1 cm。而对于电子打靶角度歧离θ：厂家没有提供推荐值，而Daryoush等［11］、Keall等［12］均认为电子打靶的角度θ设置为0°，即电子束垂直打靶；对于能谱半高宽，当FWHM的设置从0～1 MeV之间变化时，对于Varian 4 MV、6 MV、10 MV、15 MV、18 MV在水模体的百分深度剂量（Percentage Depth Dose，PDD）和不同水下深度的离轴比（Off Axis Ratio，OAR）没有明显影响［13］。而对剂量学参数影响较大的，而且最为关键的参数为入射电子打靶平均能量。

本 文 利 用 蒙 特 卡 罗 软 件 包 EGSnrc［14］/BEAMnrc［15］针对 Varian 600C、Trilogy 和 Edge FFF模式，模拟的标称能量档均为6 MV的情况下，探索不同入射电子打靶能量产生的X射线在水体模中的剂量分布，从而寻找一种快速确定入射电子打靶能量的方法。

1 材料与方法

1.1 模型的建立

模拟的医用直线加速器为Varian 600C、Trilogy和Edge，模拟的标称能量均为6 MV。建立其所对应的蒙特卡罗模型主要是在蒙特卡罗程序软件包Beamnrc进行。图1给出了Varian 600C的一个模型示意图。模型部件包括靶、初级准直器、均整器、监测电离室、灯光野镜、次级准直器。通过BEAMnrc的SLABS描述靶；CONS3R描述初级准直器；FlATFILT描述均整器；CHAMBER描述监测电离室；MIRROR描述灯光野镜；JAWS描述次级准直器。各医用直线加速器的具体几何参数和材料参数由厂家提供。

1.2 模拟参数的设置

图1 加速器模型Fig.1 Sketch map of linear accelerator

模拟计算时，计算机配备规格如下：操作系统为fedora 18（64位），内核为Linux 3.6.10-4.fc18.x86_64，CPU型号为intel core i7-4770K（3.5 GHz），内存为Kingston DDR3 8 GB，主要的输运参数设置如下：电子的截止能量ECUT=0.7 MeV，光子的截止能量PCUT=0.01 MeV，电子输运步长算法为PRESTA-II，电子过边界算法为EXACT。为提高模拟效率，采用的减方差技巧为：轫致辐射方向分裂（Directional Bremsstrahlung Splitting，DBS），分裂数（NBRSPL）为1 000，分裂野半径FS设置为射野边长的 2/2倍，全局电子射程截断能量Esave设置为2.0 MeV，钨靶的电子射程截断能量Esave设置为0.7 MeV。另外对于入射电子束参数设置为：入射电子束宽R选定为FWHM=0.1 cm的高斯分布，能谱半高宽FWHM设定为0 MeV，电子打靶角度歧离θ设置为0°。

1.3 入射电子打靶能量对剂量学参数的影响

当入射电子打靶能量分别设置为5.5 MeV、5.7 MeV、5.9 MeV 、6.1 MeV、6.3 MeV、6.5 MeV时，模拟不同型号的医用直线加速器在3 cm×3 cm、10 cm×10 cm、40 cm×40 cm所对应的相空间文件（Phase Space File，PSF），而后把 PSF作为源，用DOSXYZnrc［16］模拟计算在水体模中的剂量分布。整理比较模拟结果，探索入射电子打靶能量所产生的X射线对剂量分布的影响，寻找一种快速确定入射电子打靶能量的方法，并验证其可靠性。

2 结果及分析

2.1 入射电子打靶能量对PDD的影响

图2给出了当入射电子打靶能量为5.5 MeV和6.5 MeV时，不同机型以及所对应的不同射野下的PDD比对图。从图2中可以看出，尽管打靶能量相差1 MeV，然而PDD的谱形差异却不明显。

表1给出了当入射电子打靶能量为5.5 MeV和6.5 MeV时，不同机型不同射野下PDD模拟值的最大差异。

综合图2和表1，说明在打靶能量的可调范围内（5.5～6.5 MeV），PDD对入射电子打靶能量不敏感［17］。

表1 打靶能量分别为5.5 MeV和6.5 MeV时，不同射野下PDD模拟值的最大差异Table 1 The max differences of PDD when incident electron energies are 5.5 MeV and 6.5 MeV

图2 打靶能量分别为5.5 MeV和6.5 MeV时，不同机型不同射野下的PDD比对(a)Varian 600C 6 MV，(b)Varian Trilogy 6 MV，(c)Varian Edge 6 MV FFFFig.2 PDD profiles of different linac models and different fields when the incident electron energy is 5.5 MeV and 6.5 MeV,respectively(a)Varian 600C 6 MV,(b)Varian Trilogy 6 MV,(c)Varian Edge 6 MV FFF

2.2 入射电子打靶能量对OAR的影响

图3 给出了打靶能量为5.5 MeV和6.5 MeV的情况下，不同机型3 cm×3 cm、10 cm×10 cm、40 cm×40 cm水下深度5 cm的OAR对比，为了显示方便，3 cm×3 cm的数值都乘以0.6，10 cm×10 cm的数值都乘以0.8。从图3中可以看出，不同打靶能量下，3 cm×3 cm、10 cm×10 cm的OAR的谱形几乎重叠，而40 cm×40 cm的OAR存在明显的差异：打靶能量越低，OAR的“肩部”越高，而且不同的电子打靶能量的“肩部”差异在离轴为10～20 cm最为明显。而在其他深度下，入射电子打靶能量对OAR的影响规律，和水下5 cm的一样。说明大射野的OAR对电子打靶能量敏感［17］。

图3 打靶能量分别为5.5 MeV和6.5 MeV时，不同机型不同射野在水下5 cm的OAR比对图（为了显示方便，3 cm×3 cm的数值整体乘以0.6，10 cm×10 cm的数值整体乘以0.8） (a)Varian 600C，(b)Varian Trilogy 6 MV，(c)Varian Edge 6 MV FFFFig.3 OAR profiles at 5 cm underwater for different linac models and different fields when the incident electron energy is 5.5 MeV and 6.5 MeV,respectively(in order to display clearly,all data of 3 cm×3 cm multiply 0.6 while 10 cm×10 cm multiply 0.8)(a)Varian 600C,(b)Varian Trilogy 6 MV,(c)Varian Edge 6 MV FFF

2.3 入射电子打靶能量的确定

图4 给出了40 cm×40 cm射野条件水下5 cm离轴距离为14.5～19 cm这一范围内，水下5 cm的OAR平均值随入射电子打靶能量的变化，从图4中可以看到，打靶能量和OAR均值呈线性相关，拟合结果如表2所示。

图4 40 cm×40 cm水下5 cm处OAR的平均值随入射电子打靶能量的变化(a)Varian 600C，(b)Varian Trilogy 6 MV，(c)Varian Edge 6 MV FFFFig.4 Relationship of OAR average at 5 cm underwater of 40 cm×40 cm and the incident electron energy(a)Varian 600C,(b)Varian Trilogy 6 MV,(c)Varian Edge 6 MV FFF

表2 OAR的平均值随入射电子打靶能量变化的拟合公式（E代表能量，R代表OAR的平均值）Table 2 Fitting formula of OAR average and incident electron energy for different linac models(E represents incident electron energy,R represents OAR average)

因此通过实测在40 cm×40 cm射野条件下6 MV X射线在水下深度5 cm的OAR结果，便可利用上述拟合公式反推此医用直线加速器的蒙特卡罗建模时的电子打靶能量。表3给出了各不同机型测量的OAR平均值以及其所对应的拟合打靶能量。

2.4 医用直线加速器模拟结果

利用表3所给出的各不同机型所反推出的打靶能量作为医用直线加速器蒙特卡罗模拟时的输入，得到的结果如图5所示。从图5中可以看出，各不同机型不同射野内的PDD和OAR的模拟值与测量值之间的差异均在1%之内。

表3 利用40 cm×40 cm水下深度5 cm测量的OAR平均值拟合的打靶能量Table 3 Fitting energies for different linac models

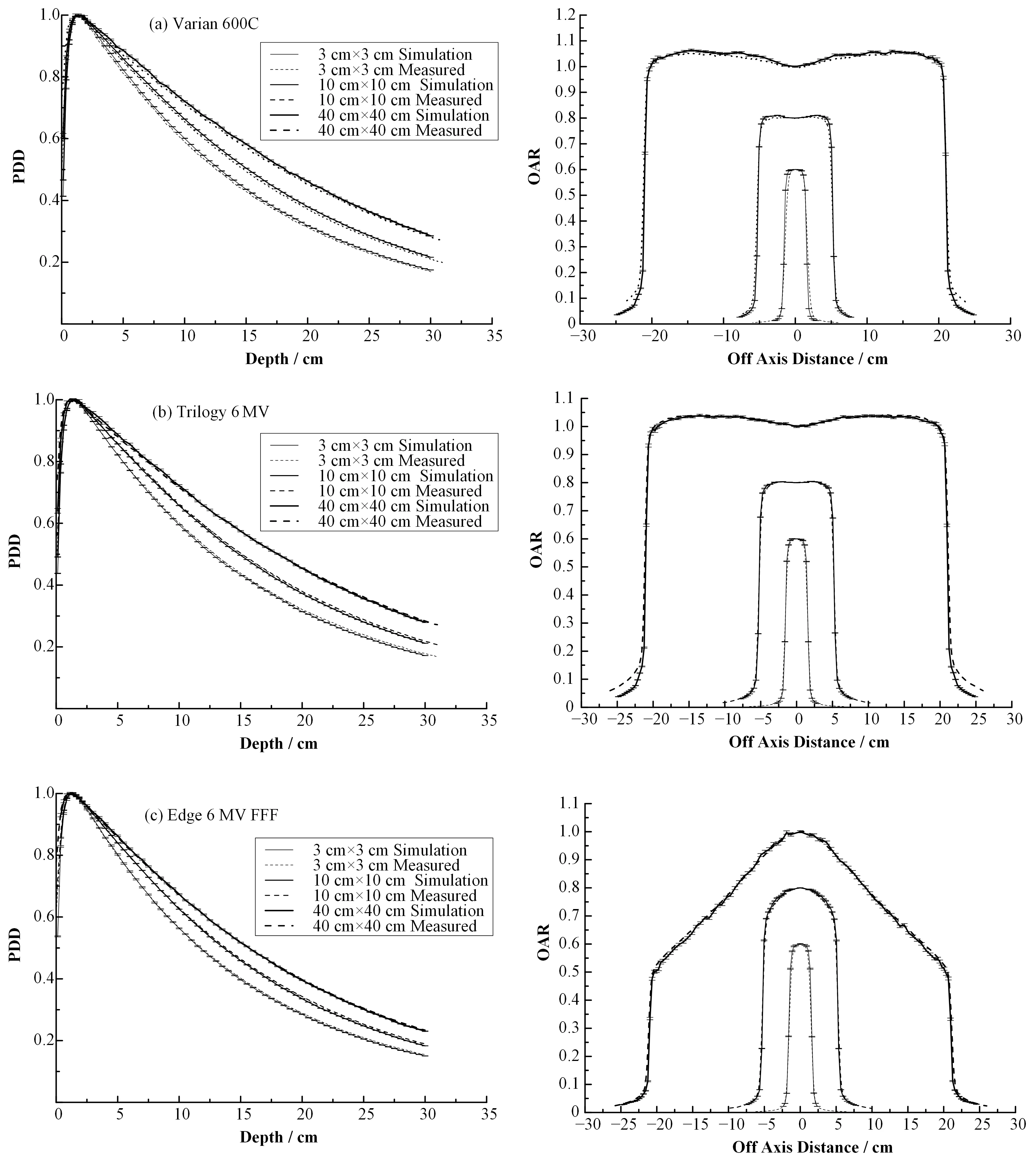
图5 各不同机型的加速器的百分深度剂量曲线（PDD）和OAR（水下5 cm处）比对(a)Varian 600C 6 MV，(b)Varian Trilogy 6 MV，(c)Varian Edge 6 MV FFFFig.5 Comparison of simulation and measurement about PDD and OAR for different linac models(at 5 cm underwater)(a)Varian 600C 6 MV,(b)Varian Trilogy 6 MV,(c)Varian Edge 6 MV FFF

3 讨论

结果表明：大射野的OAR对打靶能量“敏感”，本文通过拟合了射野为40 cm×40 cm，水下5 cm处，离轴距离为14.5～19 cm这一范围内OAR的平均值和入射电子打靶能量之间的关系，通过此关系结合OAR实测值反推入射电子束的打靶能量，以反推的打靶能量作为输入，得到的模拟结果与实测值的差异在1%之内。这表明此方法确定入射电子束的打靶能量是可行的。

医用直线加速器的靶和均整器对剂量学参数有直接和明显的影响，模拟时靶材料一般是Wu和Cu，均整器则为Cu。而Wu和Cu的质量吸收系数μen/ρ都是随着打靶能量的下降而上升。所以模拟时，当打靶能量从6.5 MeV逐渐下降时，大射野的OAR，每初始粒子所贡献的剂量也逐渐下降，但是中心轴处的剂量的下降速度要快于其他地方，离轴越远，下降越慢，因此对同一深度的点对中心轴处的点做归一时，就会出现打靶能量越低，OAR的“肩部”越高的情况。这也是大野的OAR对入射电子打靶能量敏感的原因。

4 结语

确定入射电子打靶能量是医用直线加速器蒙特卡罗模拟的关键和难点，由于大射野的OAR对入射电子打靶能量“敏感”，通过大射野的OAR测量值结合大射野的OAR与入射电子打靶能量之间的关系，根据测量结果反推模拟所需的入射电子打靶能量，可以节省调试入射电子打靶能量所需的时间。