水平循环立体车库吊篮运动不干涉条件分析及优化设计

杨剑尧 肖志权 杨政宇

武汉纺织大学机械工程与自动化学院 武汉 430200

0 引言

我国机动车保有量的迅速增加带来停车困难等问题，在城市繁华地段、写字楼、宾馆、大厦、商场、住宅小区、旅游景点等地点显得尤为明显[1]。截至2019年6月,全国汽车保有量达2.5亿辆,私家车达1.98亿辆[2]。而现有的停车设施多为简易的平面式停车场，占用了大量土地资源，不能和迅速增长的汽车数量相匹配，造成目前停车位严重缺乏的局面[3]。为了缓解停车难的问题，停车楼、升降横移类、简易升降类、垂直循环类、水平循环类停车设备相继提出。就目前机械停车设备市场而言，占用率最高的为升降横移类（75%），其空间利用率比地面式停车场有较大提高，但其利用率还不到2%。根据停车位设计要求，升降横移类空间高度不小于3.6 m，高度不够的地下停车库则不能安装。对比升降横移类，水平循环类空间利用率可提升为2.23%，且省去额外车辆横移升降通道及相关机械装置，有效提高车位容量[4,5]。水平循环类停车设备构造简单、制造成本降低、高效低耗、性价比高、对场地的适应性更强，该种停车库能很好地解决停车难的问题，有较高经济价值和社会效益。

1 工作原理

水平循环类立体车库的运行特点是采用一个水平循环运动的车位系统存取车辆，最适宜建于地形狭长的场所[6]。目前有两种形式的水平循环类停车库，即方形循环式和吊篮式。其中，方形循环式立体车库以方形运动的方式上下层车位交换，在停车系统中两头各设置1台驱动电机，可以是二层或多层。吊篮式立体车库是以圆形运动方式实现不同层位车位封闭环式的循环交换，停车系统只需设置1台驱动电机，一般适合二层。

吊篮式立体车库采用水平循环链运动方式移动载车吊篮实现车的存取，载车吊篮循环运动示意如图1所示（12车位吊篮式停车设备）。在牵引构件链条上，每隔一定距离安装一个载车吊篮，通过电机的减速转动带动传动机构[7]。在循环运动过程中，载车吊篮也将随着链条做循环运动，通过人机界面与PLC实现简单便捷的人机交互操作，控制驱动电机的正反转，从而控制载车吊篮的循环运动，实现简单方便的自动控制，从而达到存取车辆的目的。

图1 载车吊篮循环运动示意图

2 吊篮运动不干涉条件研究意义

载车吊篮做循环运动时，考虑到各吊篮之间的紧凑性，在保证空间利用率高的同时也要保证各个吊篮之间不会发生干涉，使车库正常运行。若将相邻吊篮之间距离缩小，提高了空间利用率，但在圆弧部分相邻两吊篮会发生干涉现象（见图1），反之可避免干涉，但空间利用率会降低，车库的制造成本也随之增加。吊篮的设计不仅关系车辆存放的安全，还影响到整个车库装置的运行安全，故吊篮运动不干涉条件的合理设计对整个车库装置有很重要的影响。

如图1所示，吊篮随着链条做循环运动，由于吊篮在进入圆弧部分时，水平运动速度将小于链条的运动速度，针对吊篮在圆弧部分做旋转运动时不发生干涉，且相邻吊篮之间的间距不宜过大的问题；通过对吊篮循环运动时的特性进行仿真，分析影响吊篮在圆弧部分运动时发生干涉现象的条件，并进行优化设计。

3 吊篮运动不干涉条件分析

吊篮在进入圆弧部分运动时，吊篮运动的特性分为4个阶段，对各个阶段干涉条件进行分析，并通过运动仿真及优化设计，得到合理的优化方案。为便于分析，考虑将吊篮实际的外形轮廓进行简化，将吊篮轴测图轮廓简化成矩形（见图2）。由于简化的吊篮外形轮廓已将原有外形轮廓包括，故简化后的运动规律也适用于原有的吊篮外形。

图2 吊篮轴测图轮廓简化图

3.1 吊篮运动4个阶段过程概述

通过建立参考坐标系，对吊篮0、吊篮1的4种运动位置状态进行分析（见图1），第一阶段O1沿着半径为的圆弧运动，O2保持水平向右运动，直至O2到达（0，R）点后进入第二阶段，O1、O2沿着同一圆弧运动（此时吊篮0比吊篮1更加靠右），第三阶段O1、O2沿着同一圆弧运动（此时吊篮1比吊篮0更加靠右），第四阶段O2沿着半径为的圆弧运动，O1保持水平向左水平运动。

3.2 优化设计过程

为了使两个相邻吊篮在运动过程中不发生干涉现象，对吊篮运动过程中的相关参数进行假设定义，设两相邻吊篮的上边中心O1、O2水平方向的距离为ΔX，垂直方向的距离为ΔY，要求当O1、O2之间的水平距离ΔX小于载车吊篮的宽度W时，其垂直方向的距离ΔY大于载车吊篮的高度H，即若0≤ΔX≤W时，∣ΔY|＞H，此时两个相邻吊篮就不会发生干涉现象。通过选择合适的传动系统链轮节圆半径R以及链轮齿数Z就能使吊篮之间避免发生干涉现象，优化设计过程主要由确定设计变量、建立目标函数和确定约束条件3部分组成。

1)确定设计变量

在确定设计变量时，首先确定已知量和代换相关变量，吊篮宽度W、吊篮高度H、水平运动时吊篮垂直方向上间隔的安全距离S、相邻两吊篮间隔的安全距离A均为已知量。根据实际情况选择链条节距P，即吊篮水平运动中，中心点O1、O2之间距离L、链节数N和相邻两吊篮同时运动时OO1于OO2之间的夹角θ0可以代换，其中链轮节圆半径R和吊篮0的链板旋转时，OO1与Y轴夹角θ1不能代换，故列其设计变量，即

链节数N代换为

式中：N为链节数，故N取整数。

中心点O1、O2之间距离L代换为

根据链传动分度圆计算为

链轮齿数Z代换为

相邻两吊篮同时运动时OO1于OO2之间的夹角θ0代换为

故设计变量为2个独立变量节圆半径R、吊篮0的链板旋转时OO1与Y轴夹角θ1，即

2)目标函数的建立

为了求得最佳链轮齿数Z，目标函数可以表达为

3)约束条件的确定

吊篮运动时，垂直方向相邻两吊篮之间的垂直距离(H+A)要大于圆弧直径2R，故

在吊篮链传动设计时，根据经验对链条节距P和齿数Z选择合适范围a≤Z≤b，从而对节圆半径的约束条件为

当吊篮进入第一阶段时，即O1沿着半径为R的圆弧运动，O2保持水平向右运动，此时0≤θ1≤θ0，其中，t为吊篮0在旋转角度时θ1所消耗的时间，ω为链轮的旋转角速度，v为吊篮在水平方向上的移动速度，即

即由吊篮不干涉条件为

当O1、O2的横坐标相同时为第二阶段的结束点，也是进入第三阶段的开始点，此时θ1= （ π + θ0）2。故当吊篮进入第二阶段时，即O1、O2沿着同一圆弧运动（此时吊篮0比吊篮1更加靠右），此时。即

由吊篮不干涉条件得

当吊篮进入第三阶段时，与第二阶段相似，O1、O2沿着同一圆弧运动（此时吊篮1比吊篮0更加靠右），此时。即

即由吊篮不干涉条件得

当吊篮进入第四阶段时，此时O2沿着半径为R的圆弧运动，O1保持水平向左水平运动，由于吊篮可以环形正反两个方向运动，所以第四阶段可看作是第一阶段的逆向运动，故第一阶段的运动规律适用于第四阶段。

由上述条件可对约束条件进行确定，即由式(4)得垂直方向相邻两吊篮之间距离约束函数为

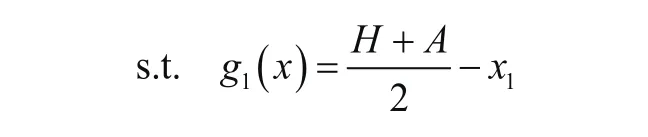
由式(5)得节圆半径约束函数为

由式(6)得第一阶段相邻吊篮运动不干涉约束函数，即当0≤x2≤θ0时

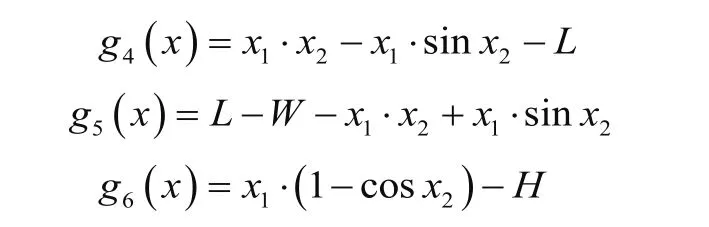
由式(7)得第二阶段相邻吊篮运动不干涉约束函数，即当 θ0≤ x2≤（π+θ0）/2 时

由式(8)得第三阶相邻吊篮运动不干涉段约束函数，即当（π + θ0）2≤x2≤π 时

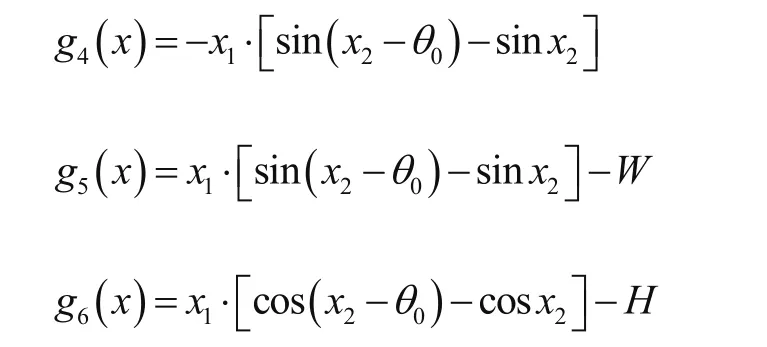
第四阶段相邻吊篮运动不干涉约束函数与第一阶段相同。吊篮0的链板旋转时OO1与Y轴夹角θ1在运动时角度变化范围为0～π，即

3.3 优化求解

利用Matlab优化工具箱对数学模型进行求解，假设已知W=2 500 mm，H=2 300 mm，S=500 mm，A=150 mm，P=460 mm，Z取10～30。其Matlab最优解主程序为

综上所述，运用优化设计方案以及数学模型，对假设实例求解，求得最优结果Z=19，满足实例吊篮运动不干涉条件以及立体车库空间利用率要求，为类似水平循环车库的结构设计提供方法参考。

4 结语

本文结合我国机动车保有量发展情况以及市场机械式立体车库使用率，通过与采用率最高的升降横移类停车设备对比，选择对场地适应性更强、空间利用率更高的水平循环类停车设备进行研究分析。针对水平循环吊篮式立体车库吊篮运动不干涉条件，通过对吊篮运动特性仿真分析，并对假设实例优化求解，给出合理的计算方法，为水平循环吊篮式立体车库结构设计以及传动系统的设计提供合理参考。