基于UG 的8 人吊篮静态性能分析

周朝朋

（200093 上海市 上海理工大学 机械工程学院）

0 引言

缆车也称空中索道,主要用途为输送游客与运输货物[1]。它凭借独特的优势，在运输市场占有一定份额，2000 年，贵州云马索道缆车公司为四川西陵雪山风景区设计了8 人缆车，这一设计标志着我国在缆车设计方面的技术已初步成熟，虽然实现了缆车技术方面的突破，但是与国外成熟的缆车技术相比，中国的缆车技术还有很长一段路要走。为了加速我国在缆车行业的发展，本文基于UG 软件分析8 人吊篮的静态性能。为今后缆车的设计提供理论和数据支持。

吊篮主要由承重梁连接件、底板梁、下横梁、立柱、上横梁、顶梁连接件、承重顶梁等组成，主要利用钢丝牵引实现游客目的地的传送，其中，吊篮主要的受力部件为立柱、上下横梁。

未来缆车的发展趋势主要有2 个方面：（1）对驱动装置进行简化，从而提高可靠性。这一优化目前已经被市场所认可；（2）考虑使用新型材料来减轻吊篮的整体质量。随着科技的发展，出现了更加优质的材料，比如生物材料、纳米材料、新型钢铁材料。有些材料的刚度和强度大而自身质量却很轻，在保证缆车质量的情况下，也实现了缆车的轻量化设计[1]。

1 吊篮的有限元模型

1.1 研究方法

8M 缆车的吊篮的结构为箱体结构，其立柱、下横梁、上横梁为等截面梁。在缆车实际的工作中，立柱会承受拉伸、拉弯等工况，故本文在UG 软件高级仿真模块中，立柱、上横梁、下横梁采用3D 扫略网格[2,3]，来模拟吊篮在实际工作中各个结构在各种工况中承受的拉伸、弯曲、扭转以及在受力情况下的应力、应变等情况。在建模过程中，三维数字模型采用自上而下的建模方式，通过建立点、线对模型进行定位然后建立模型[4]，而后对模型进行几何、位置分析，确定模型以及装配误差是否满足设计要求，通过对模型形状分析，采用不同的网格类型对模型进行网格划分。为了使分析结果更加精确，应尽量使网格细化。赋予材料属性，根据不同的工况分别定义约束、受力，进而求解结果。

1.2 工况分析

根据缆车实际工作情况，设定运行风压0.25 kN/m2，停运风压0.8 kN/m2，启动加速度最小为0.15 m/s2，工作最小制动减速度0.4 m/s2，最大紧急制动减速度1.5 m/s2。根据设定的工作状态不同，共有7 种工况：

工况1：缆车正常运行（有运行风压），受吊篮自重G，有效载荷Q（Q 指的是满负荷运行所承载的人员的总重量），运行中受到的风载荷Fwy(横向风载荷)或者Fwx(纵向风载荷)；

工况2：停运大雪（吊厢内无负荷，顶部有雪），受吊篮自重G，吊篮顶部所承受的雪载荷Ws；

工况3：停运大风（吊厢内无负荷），受吊篮自重G，运行中受到的风载荷Fwy和Fwx；

工况4：线路制动（有载有风）只用于验算吊杆吊架以及吊点连接螺栓），受吊篮自重G，有效载荷Q，运行中受到的风载荷Fwy和Fwx，人的冲击载荷H，惯性力Fa；

工况5：站内运行偏载（一半的人，作用于车厢一侧的面积），受吊篮自重G，0.5 倍的有效载荷，进站导向装置受水平力：R；

工况6：正常运行厢内冲击力（横向和纵向），受吊篮自重G，有效载荷Q，人的冲击载荷H；

工况7：1.5 倍厢体重量和人重（用于疲劳计算），受吊篮自重G，1.5 倍有效载荷。在此不作计算。

由GB 12352-2018 《客运架空索道安全规范》，力的计算公式为

2 吊篮静态性能分析

2.1 静强度分析

吊篮材料采用AL6061，许用应力[σ]=265 MPa，CAE 模型网格图如图1 所示，在结果图片中，参考第四强度理论[5-6]，显示的应力为 Von mises，在不同的工况下的不同应力如图2—图7 所示。

（1）吊篮在正常运行过程中，受到最大应力为59.56 MPa，最大应力位置在门框边架和上横梁连接处。由图2 中可以看出，应力集中在边框处，其他位置的应力较小。

（2）吊篮在停运大雪工况下，最大应力为4.525 MPa，最大应力处立柱和横梁连接处，从图3 可以看出，应力集中在横梁位置。

（3）吊篮在停运大风工况下，最大应力52.22 MPa,最大应力位置门框和上横梁连接处。在立柱的上端有应力。

（4）吊篮在紧急制动的工况下，最大应力109.13 MPa，最大受力位于门框与上横梁连接处。

图1 吊篮网格图Fig.1 Basket grid

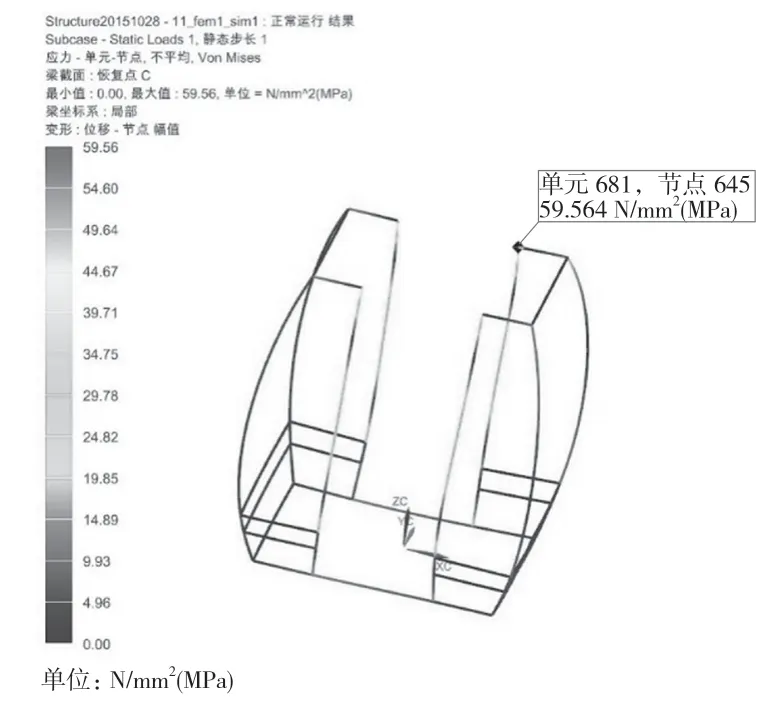
图2 正常运行吊篮应力云图Fig.2 Stress nephogram of basket in normal operation

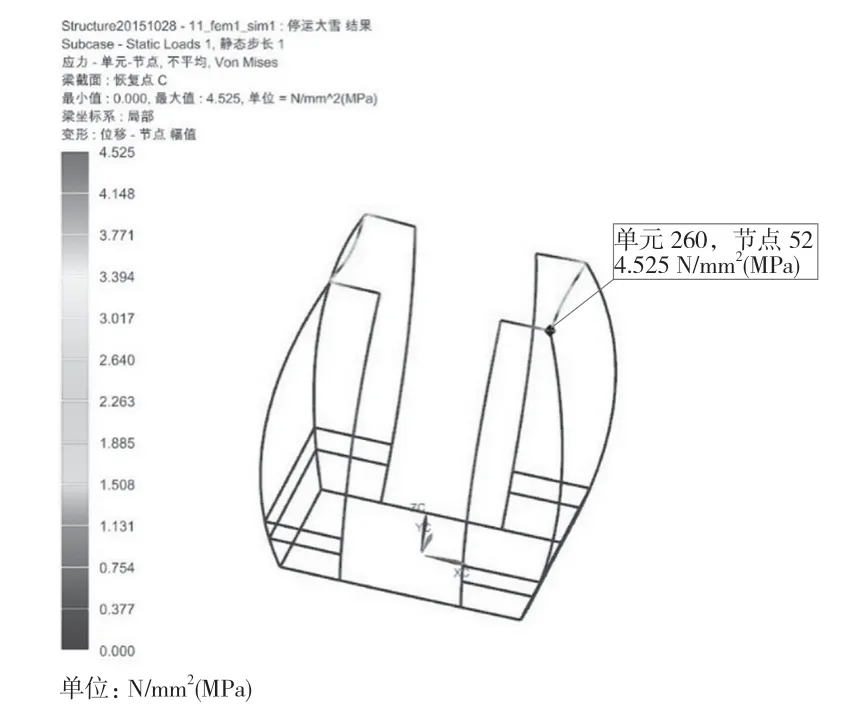
图3 停运大雪吊篮应力云图Fig.3 Stress nephogram of suspended snow basket

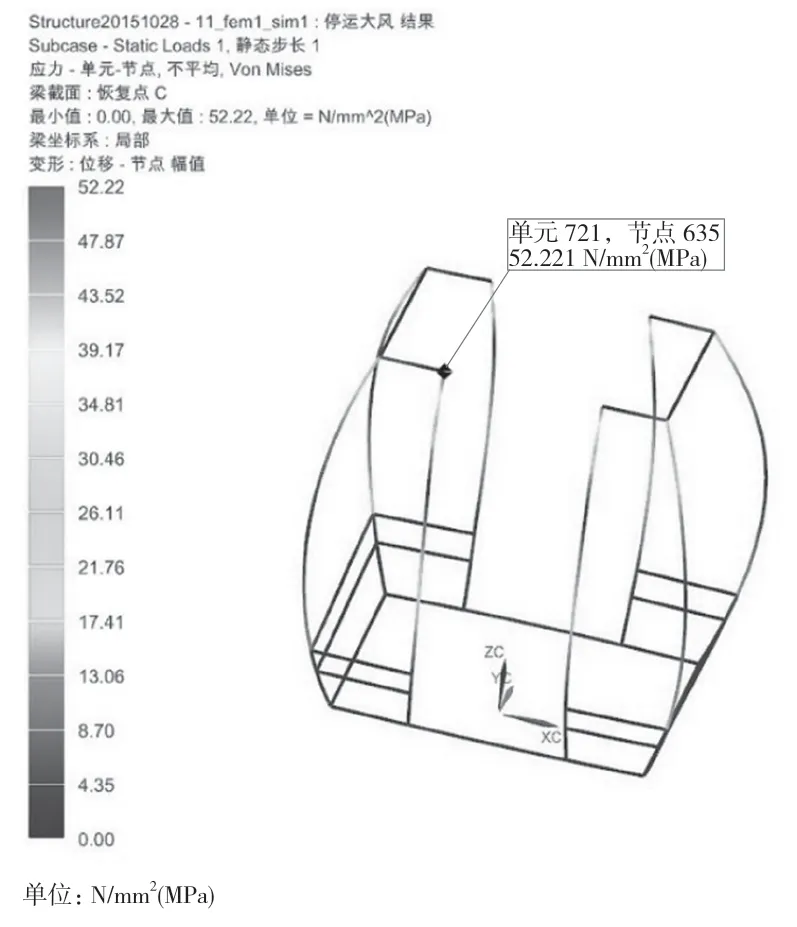
图4 停运大风吊篮应力云图Fig.4 Stress nephogram of suspended high winds crane basket

图5 线路制动吊篮应力云图Fig.5 Stress nephogram of line brake basket

（5）吊篮在站内偏载运行中，最大应力36.58 MPa，最大应力位置与紧急制动相同。（6）吊篮在1.5 倍箱内冲击，最大应力109.74 MPa，最大位置门框与上横梁连接处。

2.2 吊篮受载刚度分析

吊篮的强度分析目的主要是吊篮在工作中承受的应力，以便在之后的设计中在关键位置采取合理的设计方式，同时兼顾吊篮的质量和生产效益[7,8]。在吊篮的实际工作中，吊篮的变形也是不可忽视的部分，当变形量超过许用变形时，吊篮结构被破坏，造成不可挽回的后果。吊篮在各工况下的位移云图如图8—图13 所示。

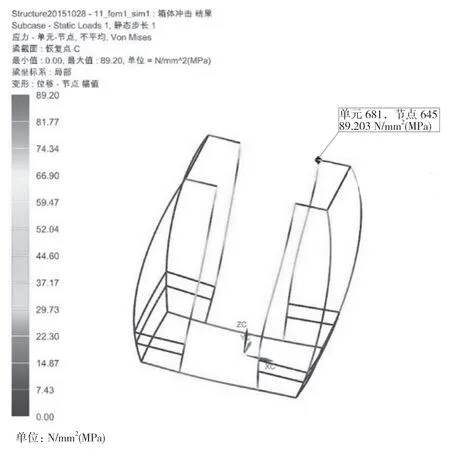
图6 站内偏载吊篮应力云图Fig.6 Stress nephogram of off-load basket in the station

图7 箱体冲击吊篮应力图Fig.7 Stress diagram of box impact basket

由图8—图13 可知，在各工况下位移分别为：2.616，0.052 1，4.832，5.568，1.342，4.308 mm。发生最大偏移的位置大多集中在门框架的中部。考虑安全因素，实际位移要小于理论计算的位移。

由吊篮的有限元计算结果可以看出，在吊篮紧急制动工况下，最大应力109.13 MPa，最大受力位于门框与上横梁连接处。材料的许用应力[σ]=265 MPa，所以结构满足静强度的设计要求。各工况下吊篮最大位移量为5.568 mm，许用位移量6 mm。故静刚度的设计满足要求。

图8 正常运行吊篮位移云图Fig.8 Displacement nephogram of normal operation basket

图9 停运大雪吊篮位移云图Fig.9 Displacement nephogram of suspended snow basket

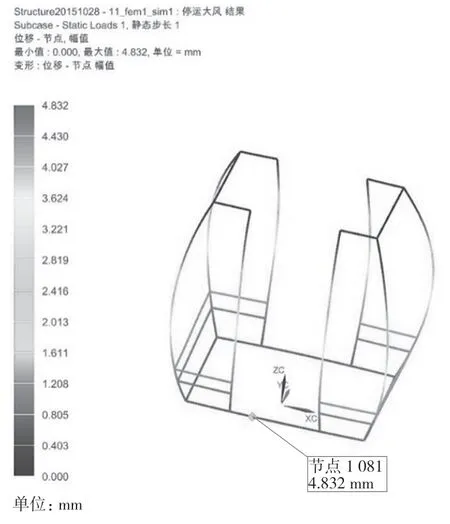
图10 停运大风吊篮位移云图Fig.10 Displacement nephogram of suspended gale basket

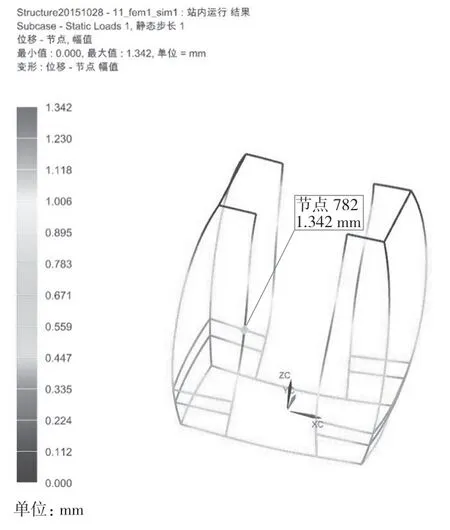
图12 站内偏载吊篮位移云图Fig.12 Displacement nephogram of off load basket in the station

图13 1.5 倍箱体冲击吊篮位移云图Fig.13 Displacement nephogram of 1.5 times box impact basket

3 结论

通过对吊篮的有限元分析，得到各工况下受到的最大应力值和最大应力值的位置，以及吊篮最大位移和最大位移的位置。由仿真结果可以看出，最大应力发生在门框架和上横梁的连接处，所以设计电缆结构时可以考虑多铆钉连接，这样既可以保证吊篮结构的强度和刚度，也不会破坏吊篮的整体结构。通过计算表明，该设计满足设计要求。